簡略化した３次スプライン曲線の生成方法

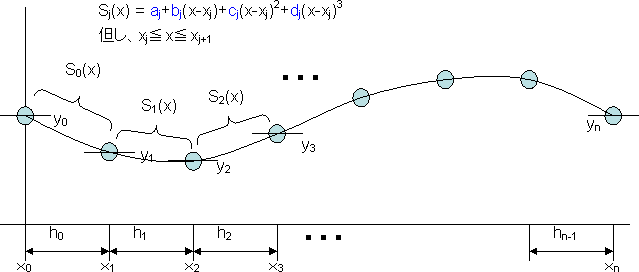
スプライン曲線とは、簡単に言えばn+1個の点を結ぶ滑らかな曲線の一種です。３次スプライン曲線は、各点と点の間を3次関数で表現し、点での接続が滑らかになるようにしたものです。

基本的なスプライン曲線

以下に単純な形のスプライン曲線の生成方法を示します。

に対してが与えられているとします。に対して、は区間で定義される関数とします。が点と点を通り（以下の前提条件の１と２）、各函数が滑らかに接続する（以下の前提条件の３と４）ように係数を決定します。なお、関数を一意に決定するために、以下の前提条件５を追加します。このを連結したものが３次スプライン曲線になります。

前提条件：に対して、

1.、
2.、
3.、
4.、
5.。

上記前提条件を元に係数を計算すると以下の通りになります。但し、です。

は以下の連立１次方程式の解になります。

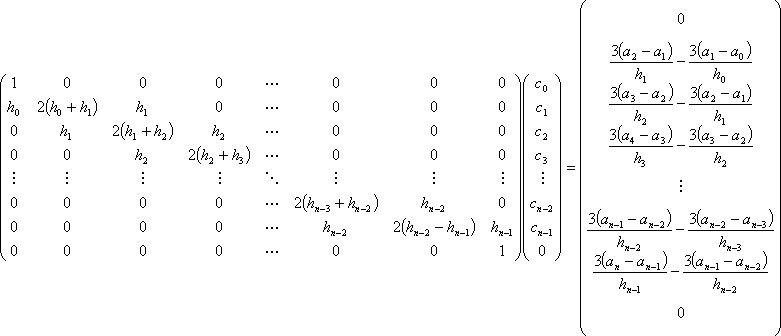
上記の連立１次方程式は、一般的な解法でも解くことが可能ですが、ほとんどの部分がゼロなので、処理を最適化すると処理がもっと単純化します（下記プログラム参照）。

ｎ次元空間上の基本的なスプライン曲線

空間上の点に対して、点を結ぶスプライン曲線を作れます。例えば３次元空間上の点の列に対してスプライン曲線を作る場合、を媒介変数として、各次元毎に分解してとなる３つのスプライン曲線を作ります。媒介変数をどうするかは、いろいろあると思いますが、安直にとするのも一例です。この場合、という特殊な条件になるので、係数の計算がより楽になります。

を計算する連立１次方程式：

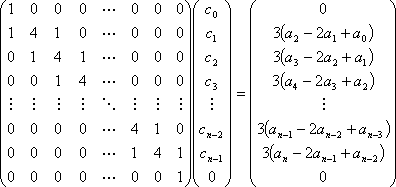
プログラム例を示します。

#define MaxSplineSize 100

class Spline {
    int num;
    double a[MaxSplineSize+1], b[MaxSplineSize+1], c[MaxSplineSize+1], d[MaxSplineSize+1];
public:
    Spline() { num=0; }
    void init(double *sp, int num);
    double culc(double t);
};

// Ｂスプライン描画
// x[num], y[num], z[num] は座標の配列
void drowSpline(double *x, double *y, double *z, int num)
{
    Spline xs, ys, zs;
    double t, m;
    xs.init(x, num);
    ys.init(y, num);
    zs.init(z, num);
    m = (double)(num-1);

    moveTo(x[0], y[0], z[0])
    for(t=0.0; t<=m; t += 0.01) {
        lineTo(xs.culc(t), ys.culc(t), zs.culc(t));
    }
}

//スプラインデータ初期化
void Spline::init(double *sp, int spnum)
{
    double tmp, w[MaxSplineSize+1];
    int i;

    num = spnum-1;

    // ３次多項式の0次係数(a)を設定
    for(i=0; i<=num; i++) {
        a[i] = sp[i];
    }

    // ３次多項式の2次係数(c)を計算
    // 連立方程式を解く。
    // 但し、一般解法でなくスプライン計算にチューニングした方法
    c[0] = c[num] = 0.0;
    for(i=1; i<num; i++) {
        c[i] = 3.0 * (a[i-1] - 2.0 * a[i] + a[i+1]);
    }
    // 左下を消す
    w[0]=0.0;
    for(i=1; i<num; i++) {
        tmp = 4.0 - w[i-1];
        c[i] = (c[i] - c[i-1])/tmp;
        w[i] = 1.0 / tmp;
    }
    // 右上を消す
    for(i=num-1; i>0; i--) {
        c[i] = c[i] - c[i+1] * w[i];
    }

    // ３次多項式の1次係数(b)と3次係数(b)を計算
    b[num] = d[num] =0.0;
    for(i=0; i<num; i++) {
        d[i] = ( c[i+1] - c[i]) / 3.0;
        b[i] = a[i+1] - a[i] - c[i] - d[i];
    }
}

//媒介変数(0～num-1の実数）に対する値を計算
double Spline::culc(double t)
{
    int j;
    double dt;
    j = (int)floor(t); // 小数点以下切捨て
    if(j < 0) j=0; else if (j >= num) j=num-1; // 丸め誤差を考慮

    dt = t - (double)j;
    return a[j] + ( b[j] + (c[j] + d[j] * dt) * dt ) * dt;
}

参考リンク

記述内容について一切保障しません。リンクは自由に行ってかまいません。
Since 2005/8/4, Final update 2004/8/15, Presented by Ishida So