台形の面積の出し方〜証明〜

その１
台形１
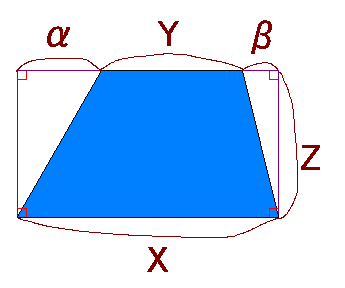
まず、台形を長方形と直角三角形にしてみましょう。
X×Z
で、台形を囲む長方形の面積が出ます。
α×Z÷2
で、左の直角三角形の面積が出ます。
β×Z÷2
で、右の直角三角形の面積が出ます。
ということは、台形の面積は
(X×Z)-(α×Z÷2)-(β×Z÷2)
ということになります。
この式を展開してみましょう。
(X×Z)-(α×Z÷2)-(β×Z÷2)=XZ-1/2αZ-1/2βZ
 =XZ-(1/2αZ+1/2βZ)
=XZ-1/2Z(α+β)
ここで、XとY・α・βの関係を見てみると
X=Y+α+β
に、なります。ということは、
α+β=X-Y
で、先ほどの式に代入できます。
 =XZ-1/2Z(X-Y)
=XZ-1/2XZ+1/2YZ
=1/2XZ+1/2YZ
=1/2Z(X+Y)
Xを「下底」と呼びます。
Yを「上底」と呼びます。
Zを「高さ」と呼びます。
したがって、台形の面積は
(上底+下底)×高さ÷２
ということになります。
戻る