音色データの構成
音色データファイル内の1つの楽器に対応するデータは、主に次の要素で構成されています。
・波形データ
音色の個性を表現するデータ。
・エンベロープデータ
音色の減衰の仕方を定義するデータ。
・ビブラートデータ
音量の揺れ具合を定義するデータ。
波形生成
wave table 音源ですので、波形生成は録音波形を元にします。
MID-Play のメインターゲットはメモリが少ない WindowsCE ですので、少しでも波形サイズを
縮めるために 8bit モノラルサンプリングの波形を利用しています。
波形データは、1度しか再生されない先頭部分と、繰り返し再生される繰り返し部分をつなげて
保持しています。
音の立ち上がりの部分は、音色の印象に大きく影響します。
たとえば、人間の音声でも「あーー」というのと「かーー」というのでは、「ー」部分では、
どちらも「あー」のような音ですが、立ち上がりは明確に「あ」「か」の違いがあります。
このような特徴を表現できるように、先頭部分だけ特別扱いにしています。
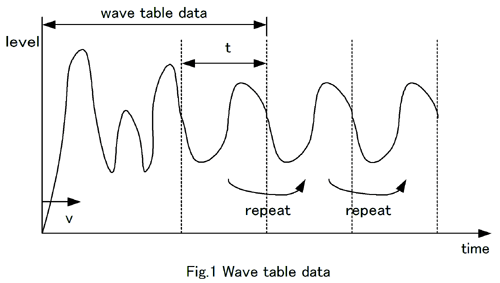
波形データは Fig.1 で Wave table data と書かれた範囲で保持しています。再生時は、必要に
応じて時間軸方向に伸長または縮小しますので、波形データ上では 1sample あたりの時間は定義
されません。
具体的に例を挙げると、たとえば、44100Hz 再生モードにおいて 440Hz の音を出したい場合に
Fig.1 の t で示される部分のサンプル数が 32sample だったとすると、伸長率は次のように求
まります。
t の区間に再生すべきサンプル数 = 44100 / 440 = 100.23sample
伸長率 = 100.23 / 32 = 3.13倍
つまり、波形データ上の 1sample が 3sample に引き延ばされるわけです。
しかし、時間軸方向にニアレストネイバー法で波形データを選択的に利用してしまうと、引き延
ばした際に Fig.2-(a) のような階段状になってしまいます。これを防ぐために、線形補間を行い
ます。
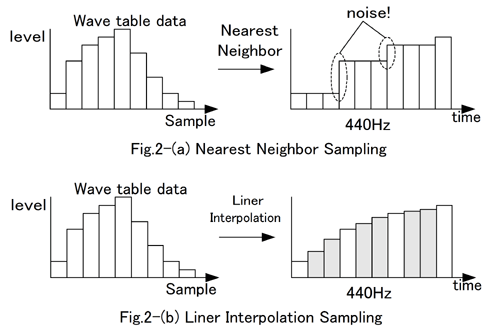
Fig.2-(b) は線形補間の例ですが、3倍に引き延ばされる場合でも、波形データ上の2サンプルの
間のデータをとりたい場合に線形補間で求めることで Fig.2-(b) のグレーのデータを得ています。
これにより波形はニアレストネイバー法よりも圧倒的になめらかになり、ノイズが軽減されます。
高速化
一般的に割り算は非常に時間がかかります。しかし、補間などを行う計算を数学で教わったとおり
に実装すると割り算だらけになってしまいます。
そこで、"再生波形が 1sample 分進むとテーブル波形がどの程度進むのか" という情報、つまり
テーブル波形の参照移動速度をあらかじめ計算してしまいます。Fig.1 の v に相当する値です。
ただ、sample 単位で単純に割り算してしまうと v は非常に小さな値になり、整数化したときに
発生する切り捨て誤差により、値が大きく異なってしまいます。それを解消するために、v は n 倍
した値を整数化して利用することにします。移動の際も v をそのまま加算して、波形を参照する
ときに nで割り、それを位置とします。
「割り算をなくすために v を用意したのに、それをまた割るの?」と思うかもしれませんが、n を
プログラム作成段階に決められることが、元の割り算と違う点になります。n は 256 とか 1024
などの 2 の累乗にしておけば、1/256 や 1/1024 は割り算ではなく右シフトで実現できることに
なります。
以後、この方式を固定小数点数と呼ぶことにします。というのも x[bit]の数値のうち、下位y[bit]
を小数部と見なす「小数点位置が固定」の実数値であると見なせるからです。1/256 の場合、小数
点以下 8[bit]の精度をもつ固定小数点数ということになります。
線形補間の実現方法
波形データの参照サンプル位置情報は、64bit整数を使います(VisualC++ なら __int64)。
このうち、上位 32bit が実際のサンプル位置、下位 32bit がサンプル位置の小数部になります。
たとえば、0x0000 0001 8000 0000 だとすれば、サンプル位置 1 と 2 のちょうど中間あたりという
意味になります。
( 0x80000000 は 1/2 の位、040000000 は 1/4 の位・・となるため)
この方式の場合、次のような方法で整数部および小数部を取り出せます。
整数部 = *(((__int32*) &U64Value) + 1)
小数部 = *((__int32*) &U64Value)
※リトルエンディアンの CPU に限る。ビッグエンディアンの場合は 整数部と小数部の表現が入れ
替わる。
ターゲットマシンが 32bit CPU なので、64bit で処理してしまうとコンパイラによっては無駄な
演算を生成してしまいますが、上記のように 32bit しか必要ない旨をソース上に明記することに
より、コンパイラも無駄な演算を生成しなくなります。
特に、WindowsCE のようにターゲットCPUが定まらないような場合は、メンテナンスや動作確認の
観点からアセンブラで記述することもできないため、このような記述は有効だと思います。
マクロ化しておくと、それほど難解なコードにはならないので便利です。
#define GET_HI_DWORD(U64) *(((__int32*) &(U64)) + 1)
#define GET_LO_DWORD(U64) *((__int32*) &(U64))
線形補間を行う場合、位置情報変数を Pos とすれば、次のような演算で処理できます。
32bit 演算で桁あふれが発生しないように、重みは上位 16bit のみ利用しています。
重み = GET_LO_DWORD(Pos) / 65536;
線形補間結果 = { Wave[GET_HI_DWORD(Pos)] * ( 65536-重み ) + Wave[GET_HI_DWORD(Pos)+1] * 重み } / 65536;
これは次のように置き変えることで割り算は無くなり、かけ算も1つに減ります。
重み = GET_LO_DWORD(Pos) >> 16;
線形補間結果 = Wave[GET_HI_DWORD(Pos)] + [{ (Wave[GET_HI_DWORD(Pos)+1] - Wave[GET_HI_DWORD(Pos)]) * 重み } >> 16];
GET_HI_DWORDマクロは、+1 などの演算がありますがコンパイル時に評価できる演算のため Pos
変数参照の時間しかかかりません。
Wave[] の参照は、Wave[] 自体が音色の数だけ存在するため、最初の1回目はキャッシュミスヒット
になる可能性がありますが、残り2つは同一アドレス・隣接アドレスのため同一キャッシュラインに
収まっている場合の方が一般的なため、高速です。加算、減算、シフトはいずれも 1cycle で処理で
きる演算のため高速です。
エンベロープ
波形テーブルには、音声の高周波成分情報しか含まれていません。立ち上がり時の特徴部分と、繰り
返し部分の1周期(場合によっては数周期)分だけです。人間が音程としてではなく、音の減衰として
感じるような低周波成分は、含まれていません。
音の減衰は、NoteOn, NoteOff のタイミングによって決まります。演奏する曲、それどころか音符長・
テンポ等によって変化するため、無限にあるとおもわれるこれら全ての組み合わせについて録音して
おくことは不可能です。そこで、簡単な演算により、音の立ち上がりからピークまでの速度、ピーク
から減衰変化点までの減衰速度、減衰変化点からの減衰速度、NoteOff からの減衰速度、といった具合
にパラメータを用意して、波形テーブルとは独立して低周波成分波形を生成しています。これをエンベ
ロープと呼んでいます。波形のイメージを Fig.3 に示します。
減衰速度は、加速度をもたない定数にしてあるため、角張った波形になりますが変化点は数個しかない
ため、(私の主観レベルにて)気になるほどのノイズにはなりませんでした。
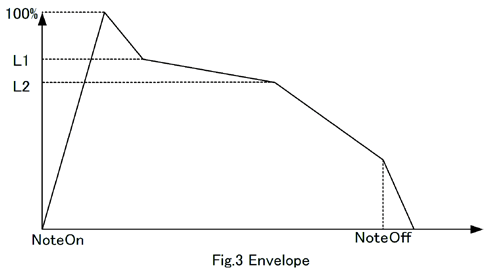
エンベロープの波形は、波形データが作る波形よりも遙かに低周波の波形になります。
エンベロープ波形の立ち上がり部分(Fig.3で左端に相当)は音が聞こえ始めるタイミングで、波形が
消滅する部分(Fig.3で右端に相当)は音が聞こえなくなるタイミングです。
一方で、波形データが作る波形は、繰り返し部分は1秒間に数百〜数千回も繰り返すほど短い波長になり
ます。Fig.1 と Fig.3 では時間軸のスケールがかなり異なるので注意してください。
MID-Play では、エンベロープ波形データを1楽器につき1つだけ定義できるようになっています。そのた
め、場合によってエンベロープ波形を変更しなければならないような楽器は表現できません。
エンベロープデータは、折れ線が折れ曲がるレベル(L1, L2)と、そのレベルへ到達するまでのレベル軸方
向の速度を各折点ごとに保持しています。NoteOff点におけるレベルは定義されておらず、時間的にNoteOff
が要求された時点で、レベル0 へ向かう速度を変更します。
そのため、NoteOffが発生する前に音が消えて無くなる場合もあります。
ビブラート
音量方向あるいは周波数方向に揺らぎを持たせると心地よい音になりますが、MID-Play では音量方向に
正弦波波形にて揺らす機能を持たせてあります。音の立ち上がり時には揺れレベル0 (揺れ無し)で、徐々
にレベルn へ向かい、レベルn に到達したらそこで安定して揺れ続けるというビブラートです。
MID-Play2 の音色データには周波数方向の設定値も含んでいます。
[前へ][▲上へ][次へ]
Copyright (C)2004 t.hara, 無断転載禁止