OPLL互換回路 F-Number 値
※情報の正確さは保証できません。
F-Number の値の謎
MSX の資料を見ていると、誤植の多いのが F-Number の値です。
「MSX2+パワフル活用法」「MSX-Datapack volume2」「MSXturboRテクニカルハンドブック」の全てで、記載されている
数式が異なっています。
F-Number とは、音色ではなく、音程を決めるパラメータの一つで、これを間違えると音痴な演奏になってしまいます。
見比べてみると、「MSXturboRテクニカルハンドブック」に記載の数式が最も正しいように思いますが、いまいち自信が
持てません。早速、VM2413 を解析して、真偽を確かめることにします。
MSX-Datapack volume2 を見てみると、次のような式で表現すると書かれています。
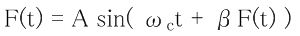
F(t) は再生周波数で、F(t) を決めるのに F(t) を使うという不思議な式です。
帰還回路(フィードバック回路)だと書かれているので、実際は式2 のようなイメージだと思います。
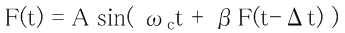
式中に sin() が出てきますが、回路では SineTable という変換テーブルで sin() 値を生成しています。
SineTable のサンプリング分解能は、512 で 2π[rad] という値で、512 = 2^9 だということを覚えておいてください。
そのサンプリング分解能でサンプリングした sin波は次のグラフになります。
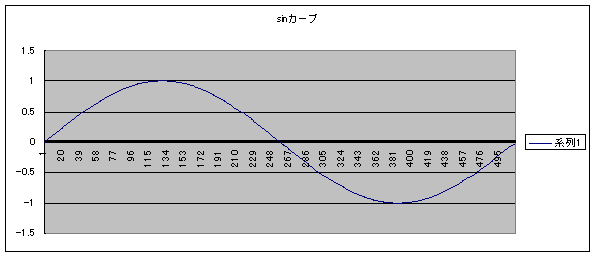
SineTable を単体で動かしたときの出力波形は次の写真になります。
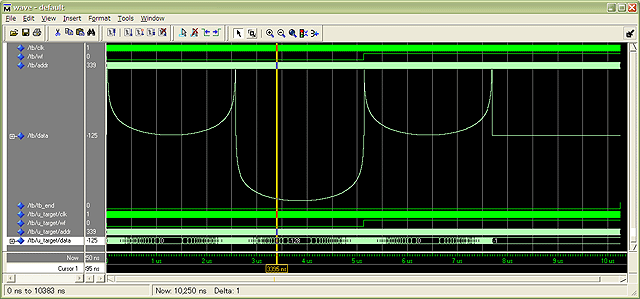
SineTable のカーブは、実際の sin波よりもポッチャリしてるのと、常にカーブの凸の向きが同じです。
この謎の答えは、LinearTable にありました。
VM2413 は、内部で対数的な数値を扱っていますが、出力直前に線形に変換しています。その変換テーブルが LinearTable
で、簡単に言うと log() の逆変換に相当することをしています。ただし、絶対値に対してかけています。
これをふまえた sin波のサンプリング波形は次のグラフになります。
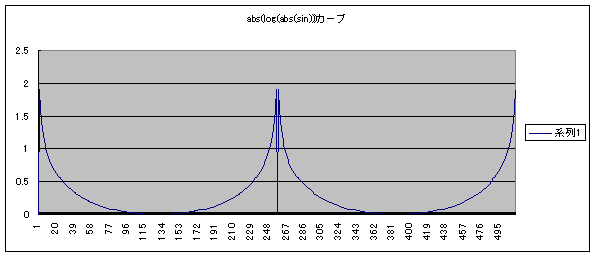
回路の出力とカーブの形が一致しました。
さて、F-Number の意味を知りたいので、sin の引数に入っていきます。
SineTable は Operator の中でインスタンスされており、位相指定は addr ポートで受け取ります。
いくつかの特殊な音色(リズムの SD, TOM)は、専用の回路で addr を決めているようですが、
一般的な音色では、PhaseGenerator によって addr 値(位相位置)が決まるようです。
PhaseGenerator は、PhaseMemory というメモリを持っており、各チャネル(9チャネルある) の値を保持しています。
1チャネルごとに2値を保持しているようです。
slot という状態変数が、0 と 1 のときにチャネル0, 2 と 3 のときにチャネル1 ... 16,17 のときにチャネル8 という
割り当てであり、この slot がそのまま PhaseMemory のアドレスに接続されています。
PhaseMemory に書き出す値は、PhaseMemory の同じアドレスから読み出した値に dphase を足した値です。
PhaseMemory を Pslot(t) としたときの式は次のようになります。t はサンプリングタイミング時刻(実行サイクル数)
として、dphase を Δp と表現すると、次のような式で表せます。
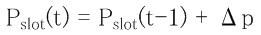
P(t-1) が P(t) に含まれているのでフィードバック系です。
IIR フィルタとして見た場合、係数が 1 なので、減衰せずにいつまでも昔の状態を引きずります。
これでは、たとえば音色が変化した場合とか、音程が変化した場合におかしなことになるので、その対策も入れられており
key 信号の立ち上がりエッジ(たぶん、音色の鳴り始め)で P(t) = 0 に置き換わるような回路が入っていました。
では、dphase はというと、次のような演算を行う回路で構成されています。
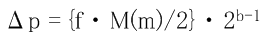
f はチャネルの F-Number, m はオペレータの MULTI, b はチャネルの Block のレジスタ値が対応しています。
M() は、MULTI を係数に変換するための変換関数(回路では単純な変換テーブル)です。
"/ 2" は、M() を目的の倍率に戻すための係数です。M()=1 なら 1/2倍, M()=8 なら 4倍 ... といった具合です。
残りの "/ 2" は、以降の計算回路の回路規模を小さくするための細工でしょうか!?、ちょっと謎です。
ということで、やっとお目当ての F-Number が登場しました。そのまえに回りの信号も簡単に触れておきましょう。
Δp は位相変化量ですが、別の言い方をすれば、P(t) の微分値であり、P(t) の進行速度でもあります。sin波という観点では角速度ωとも言えます。
つまり、Δp が2倍になるということは、波長が半分になるとか、周波数が倍になるという意味であり、
音的には1オクターブ上がることになります。
Block = 0 のときと、Block = 1 の時では、Block = 1 の方が1オクターブ高いわけで、すなわち Block はオクターブ
そのものを指定するモノといえます。値としては 3bit なので 0〜7 を指定できます。
MULTI は、4bit なので 0〜15 の値をとります。これは、変換関数 M() によって、次の値に変換されます。
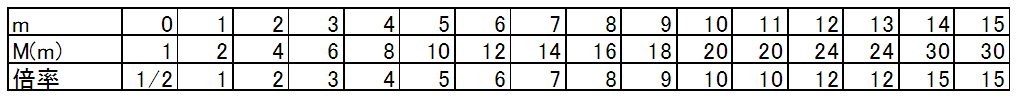
MULTI は、位相変化量の倍率であるため、MULTI=2 にすると倍音(1オクターブ上)。MULTI=4 にすると4倍音(2オクターブ上)。
の音に変更することになります。
2オペレータあり、一つは搬送波(キャリア)、もう一つは変調波(モジュレータ)になっています。
キャリアが音色の音程を決める周波数を決めるため、キャリアの MULTI を大きな値にすると高い音の音色にすることが出来ます。
モジュレータは、キャリアの位相に対して加算する波形になるため、MULTI の指定で音の雰囲気が変わります。
ここでやっと本題の F-Number です。
ここまでの解析結果から、もう明白ですね。
Δp を決めるための主要成分であるため、これも音程を決める要素です。
いくつかの資料には、「F-Number は1オクターブ内限定の設定しか出来ません」と書かれていますが、そんなことはありません。
位相の増分なので、小さくすると音程が高くなり、値を半分にすると1オクターブ上がります。
ただし、小さくなるほど正確な値を表現できなくなるので、F-Number だけで音程調整をすると、高音部が音痴になってしまいます。
これを避けるために用意されているのが、Block です。
本当は、もっと多くのビットを F-Number に割り当てれば Block なんてパラメータは必要ないのですが、
そこは古い回路です。1ビット大きくなって、レジスタ用FFや、演算回路のビット幅が大きくなることによって、回路の肥大化を
避けたかったのでしょう。F-Number (仮数部) と Block (指数部) の 12bit 浮動小数点数を採用していると言えます。
浮動小数点数といっても、F-Number 値は正規化されていないし符号部もないので、PC の CPU が搭載するやつとは若干違います。
SineTable の話を思い出してください。sin波は、2^9 で一巡するようなテーブルになってました。
Δp = 1 になるように設定すると、1波長分が出終わるまで 512サンプルかかるということです。
では、1サンプルとはどんな時間なのか?
OPLL には、18個のオペレータが内蔵されていて、それらを時分割で処理しています。
つまり、演算回路は1組しかないのに、全オペレータで順繰りに使うことで 18個のオペレータ出力を得ています。
この「どのオペレータを処理してるところですか?」を示す信号が slot です。
次に、1つのオペレータの中も 4サイクルに別れています。その何番目かを示す信号が stage です。
波形の更新サイクルは、stage = 2 のサイクルだけです。
1つのオペレータに着目したとき、そのオペレータ専用の stage = 2 が来るタイミングは、
18スロット * 4ステージ = 72 であることから、72サイクルに1回です。
MSX に搭載された場合、CPU クロックで動作するため、1サイクル = 3.579545MHz です。
これがさらに 72分周されるため、およそ 49.716kHz の周期であることが分かります。
仕組みが分かったところで、具体例を挙げて計算してみます。
440Hz の音を出したい場合。F-Number や Block にはどんな値を指定すればいいのか?
1周期が 512 であるので、これが秒間 440 回発生するには、秒間何回サンプリングすればいいかというと
512 * 440 = 225280回
です。
サンプリング周期は、およそ 49.716kHz。正確にするために 3579545 / 72 Hz とします。
サンプリング周期=1秒間にサンプリングする回数なので、それを上回る分は読み飛ばす=Δp にすればいいわけです。
Δp = 225280 / ( 3579545 / 72) = 16220160 / 3579545 ≒ 4.5315
あれ!?数値が小さすぎる。
PhaseGenerator を注意深く見てみると、pgout に出力する際 CONV_PGOUT なる関数を通過しているのが確認できます。
中身を見てみると、シフタでした。
pv(PHASE_TYPE'high downto PHASE_TYPE'high - PGOUT_TYPE'high)
PHASE_TYPE'high は 17, PGOUT_TYPE'high は 8 であるため、17-8 = 9 で、9bit 右シフトしてます。
これを考慮して、上のΔp の計算式を修正。
Δp = 225280 * 512 / ( 3579545 / 72) = 8304721920 / 3579545 ≒ 2320.01
9bitのシフトは、固定小数点数扱いで小数部 9bit 持たせることにより、Δp の精度を上げているのが目的ですね。
サンプリングの位置が多少ずれても問題ないので、サンプリングデータは最小限の 512 要素に減らして回路規模を
抑え、位相計算は 512*512 サンプルの分解能で処理していると言ったところです。
PhaseGenerator の出力である pgout は、サンプリング用なので、さっさと 9bit 削ってしまっていますね。
Δp の段階で削らないのは、精度を維持するためです。
で、Δp が求まったので、今度は Block と F-Number に分離していきます。
F-Number = Δp / (2^(Block - 1))
であるため、Block = 4 (オクターブ4) にすると、
F-Number = 2320.01 / 8 ≒ 290.00
となります。
ここで、数式を一般化します。
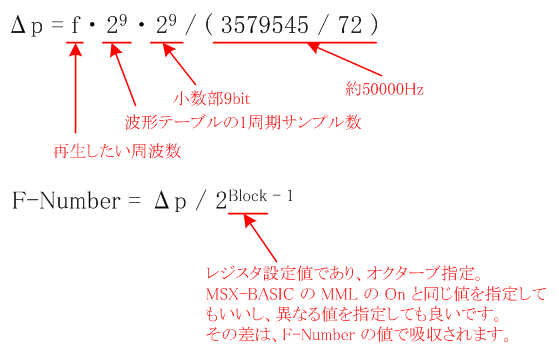
最初の話に戻りますが、「MSX2+パワフル活用法」「MSX-Datapack volume2」「MSXturboRテクニカルハンドブック」
の3つの資料に掲載されている F-Number を求める式ですが、正しいのは、MSXturboRテクニカルハンドブックに掲載
の下記の式です。
F-Number = (440 * 2^18 / 50000 ) / 2^(4-1) = 288
50000 と言うのが大ざっぱすぎる点を除けば、数式的には一致してますね。
※ 50000 ≒ 3579545 / 72
[▲上へ]