F-Number 資料
※情報の正確さは保証できません。
F-Number の解析結果をもとに、もう少し波形を掴みやすいイメージでまとめておきます。
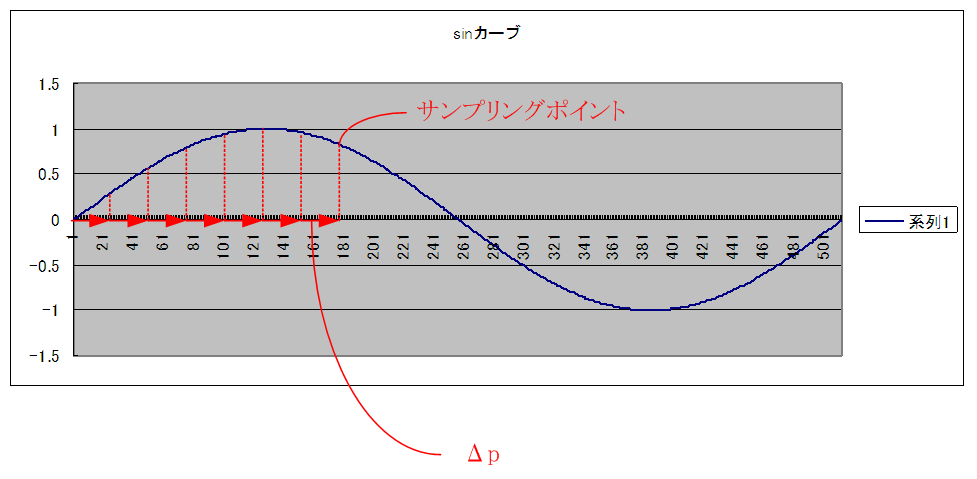
OPLL 内部には、sin波のテーブルがあります。
これは、512サンプルで1周期となる波形になっています。
出力波形の基準周波数は、この波形を伸縮することで決定されています。
伸縮の際に波形をサンプリングするわけですが、そのサンプリングポイントを P とします。
P は、約50kHz の周期で更新されてゆきます。
更新の際に、ΔP だけ加算されます。
ΔP は、(F-Number << (Block - 1)) / 512 な値です。F-Number と Block には整数しか指定できませんが、「/ 512」の除算があるおかげで
ΔP 自体は実数値となります。
(※回路的には 小数部 9bit の固定小数点数で実現されているだけで、除算回路が入っているわけではありません。)
f Hz の音を再生したい場合。
sin波一周期である 512サンプルが、1秒間に 440回まわらなければならないので、秒間の必要サンプル数(波形上の粒度)
としては f * 512 サンプルになります。
実際の出力サンプリングレート(更新間隔)は、約50kHz なので、出力サンプリングレート1に対する波形上の粒度でのサンプル値
は、f * 512 / 50k となります。
波形上の移動量 ΔP は、(f * 512 / 50k) となります。
上に書いたように ΔP = (F-Number << (Block - 1)) / 512 であることが分かっているので、(F-Number << (Block - 1)) / 512 = (f * 512 / 50k) となります。
これを F-Number について解くと、
F-Number * (2 ^ (Block - 1)) = (f * 512 / 50k) * 512
F-Number = (f * 512 / 50k) * 512 / (2 ^ (Block - 1))
F-Number = (f * 512 * 512 / 50k / (2 ^ (Block - 1))
F-Number = (f * (2 ^ 18) / 50k) / (2 ^ (Block - 1))
と言った具合にまとまります。
これじゃ、sin波の再生じゃないか!と思われるかもしれませんが、全くその通りです。
実際には、サンプリング位置 P を前後に動かすパラメータが別途存在していますが、前後に揺らすだけなので
基準となる周波数は、ここで求めた式で問題ありません。
前後に揺らすパラメータを使うことで、音色として複雑な音を再現できるようになっています。
それについては、別途。
[▲上へ]