|
倲乵倱倕們乶帪娫偵兤乵倰倎倓乶偩偗夞揮偡傞暔懱偺妏懍搙偼 丂乮幃侾乯冎亖兤乛倲乵倰倎倓乛倱倕們乶 堦夞揮乮俀兾乵倰倎倓乶乯偡傞偺偵偐偐傞帪娫傪俿乵倱倕們乶偲偡傞偲 丂乮幃俀乯冎亖俀兾乛俿乵倰倎倓乛倱倕們乶 夞揮敿宎偑倰乵倫倣乶偺偲偒丄堦廃偺嫍棧偼俀兾倰乵倫倣乶偩偐傜丄堦廃偡傞偺偵偐偐傞帪娫偑俿乵倱倕們乶側傜偽丄[嫍棧]亖[懍搙]亊[帪娫]丂佀丂[懍搙]亖[嫍棧]乛[帪娫]傛傝丄夞揮婳摴偺愙慄曽岦偵岦偐偆暔懱偺堏摦懍搙偼 丂乮幃俁乯倴亖俀兾倰乛俿亖倰乮俀兾乛俿乯乵倫倣乛倱倕們乶 幃俀傪幃俁偵戙擖偡傞偲 丂乮幃係乯倴亖倰冎乵倫倣乛倱倕們乶 丂乮幃俆乯冎亖倴乛倰乵倰倎倓乛倱倕們乶 摍妏懍搙墌塣摦偡傞応崌丄岦怱椡俥倝偲墦怱椡俥倧偼偮傝偁偭偰偍傝丄偦傟傜偺戝偒偝偼 丂乮幃俇乯俥倝亖俥倧亖倣倰冎^俀 幃俇偵幃俆傪戙擖偡傞偲 丂乮幃俈乯俥倝亖俥倧亖倣倰乮倴乛倰乯^俀亖倣倴^俀乛倰乵俹倎乶 偲偙傠偱丄乵椡偺戝偒偝乶亖乵幙検乶亊乵壛懍搙乶偩偐傜 丂乮幃俉乯俥亖倣倎 幃俇丄幃俈偲幃俉傪斾妑偡傞偲俥偼俥倝乮傑偨偼俥倧乯偵懳墳偡傞偐傜 丂乮幃俋乯倎亖倰冎^俀亖倴^俀乛倰乵倫倣乛倱倕們^俀乶 偲偄偆偙偲偑暘偐傝丄摍懍墌塣摦偱偼幃俋偱帵偡傛偆側壛懍搙偑暔懱偵敪惗偟偰偄傞偙偲偲側傞丅 偱偼丄偙偺壛懍搙偲偼壗傪昞偟偰偄傞偺偐丠 丂暔懱偵壛懍搙偑惗偠偰偄側偄偲偒丄暔懱偼惷巭偟偰偄傞偐姷惈偺嶌梡偵傛偭偰摍懍捈慄塣摦傪偟偰偄傞丅摍懍墌塣摦偼偙傟傜偺偳偪傜偵傕奩摉偟側偄偺偱丄妋偐偵壛懍搙偑敪惗偟偰偄傞偙偲偼娫堘偄側偄丅 丂摍懍墌塣摦偟偰偄傞暔懱偼姷惈偺嶌梡偵傛偭偰墌婳摴偺愙慄曽岦偵摦偒懕偗傛偆偲偡傞偑丄壛懍搙偑敪惗偟偰偄傞偨傔偦偺塣摦曽岦偑曄壔偡傞丅偁傞弖娫偺暔懱偺塣摦傪懆偊傟偽丄暔懱偼墌婳摴偺撪懁傪岦偔傛偆偵堏摦曽岦偑廋惓偝傟丄偙偆偟偨塣摦曽岦偺廋惓偺楢懕宯偑摍懍墌塣摦偵側傞丅 丂偦偟偰墌婳摴偺撪懁傪岦偔傛偆側堏摦曽岦偺廋惓傪傕偨傜偟偰偄傞傕偺偑丄偙偺暔懱偵敪惗偟偰偄傞壛懍搙偱偁傝丄偦偺敪惗尮偑岦怱椡偱偁傞丅 丂側偍丄墦怱椡偼偙偺偲偒岦怱椡偲摨偠戝偒偝偱斀懳岦偒偵敪惗偟偍傝丄崌椡偲偟偰偼姰慡偵懪偪徚偟偁偭偰偄傞偑丄壛懍搙偼巆傞丅乽崌椡侽側偺偵壛懍搙偑偁傞丠乿偲偄偆偺偼晄壜夝偵傕巚偊傞偑丄偦傟偑乽墌塣摦乿偲偄偆傕偺偺摿庩側惈幙偱偁傞偲丄偙偺応偱偼愢柧偟偰偍偔丅 丂偝偰丄墌塣摦偡傞暔懱偵偼婳摴偺撪懁傪岦偔壛懍搙偑敪惗偡傞偙偲偑暘偐偭偨丅 丂偲偙傠偱僷僱僉僢僩偱偼丄僷僱儖偵摥偔椡偺戝偒偝偲岦偒偼丄幚尡幒偱愒偄栴報乮嶰妏宍乯偵傛偭偰昞偝傟傞偙偲偲側偭偰偄傞偑丄俥亖倣倎偱偁傞偙偲偐傜傕柧傜偐側傛偆偵椡偲壛懍搙偼斾椺娭學偵偁傞偺偩偐傜丄偙偺栴報偼摨帪偵壛懍搙偺戝偒偝偲岦偒傪昞偟偰偄傞偲夝庍偟偰傛偄丅 丂傑偨壖愢偲偟偰丄僷僱僉僢僩偵偍偄偰椡偲偼扨弮偵壛懍搙偵學悢傪妡偗偨傕偺偲偟偰撪晹偱張棟偝傟偰偄傞偺偱偼側偄偐偲悇嶡偡傞丅 丂偙偺応崌丄墌塣摦偡傞暔懱偵偮偄偰偼丄椡偼岦怱椡偲墦怱椡偺俀偮偑偁傞偑丄壛懍搙偼夞揮偺撪懁傪岦偔傕偺偟偐懚嵼偟側偄丅壛懍搙傪偦偺傑傑椡偲偟偰抲偒姺偊偨帪揰偱丄墦怱椡偺奣擮偑敳偗棊偪丄暔棟僔儈儏儗乕僔儑儞偲偟偰嵟弶偺晄旛偑惗偠傞偙偲偲側傞丅 丂側偍丄僷僱僉僢僩偵偍偄偰墦怱椡偑嶌梡偟側偄偙偲偼丄僼儕乕僕儑僀儞僩偱愙懕偝傟偨僷僱儖傪夞揮偝偣傞幚尡偵傛偭偰妋擣偱偒傞丅杮棃丄暔懱傪墌塣摦偝偣傞偨傔偵戞堦師揑偵昁梫側椡偑岦怱椡偱偁傝丄偙偺岦怱椡偵懳峈偟偰敪惗偡傞斀嶌梡偺椡偑墦怱椡偱偁傞丅岦怱椡偼暔懱傪巟偊傞傕偺偵崉惈乮曄宍偡傞偙偲偵掞峈偡傞惈幙乯偑偁偭偰弶傔偰敪惗偟偆傞椡偱偁傞丅僼儕乕僕儑僀儞僩偼崉惈偺掅偄乮奜椡偵懳偟偰曄宍偟偆傞乯暔懱偲尒側偣傞偺偱丄偦偺愭偵僷僱儖傪宷偄偱墌塣摦偝偣傟偽丄偦偺敿宎丒夞揮懍搙偱墌塣摦偝偣傞偺偵昁梫側岦怱椡偑廫暘偵敪惗偣偢丄僷僱儖偼奜懁偵峀偑傞偼偢偱偁傞丅偟偐偟幚尡寢壥偱偼丄夞揮敿宎偑彫偝偔側傞傛偆撪懁傊偲嫹傑偭偰偟傑偆偺偱偁傞丅 丂僷僱僉僢僩偵偍偄偰偼丄墌塣摦偱偼岦怱椡偲偦傟偵敽偭偰敪惗偡傞壛懍搙偺傒偑峫椂偝傟偰偄傞傕偺偲偟偰峫嶡傪懕偗傞丅 丂帋偟偵墌摏傪嶌偭偰夞揮偝偣偰傒傞偲撪岦偒偵栴報偑怢傃偰偄傞偙偲偑妋擣偱偒傞丅偙傟偑懄偪岦怱椡丄傑偨偼偦傟偵傛偭偰敪惗偟偨壛懍搙傪昞偟偰偄傞偺偱偼側偄偩傠偆偐丠 丂偩偲偡傟偽丄僷僱僉僢僩偱偼彮側偔偲傕岦怱椡偵娭偟偰偼偒偪傫偲僔儈儏儗乕僔儑儞偑峴傢傟偰偄偦偆偱偁傞丅 丂偟偐偟丄栤戣偼偙偙偐傜偱偁傞丅 丂墌摏偺墢傪奜岦偒偵愜傝嬋偘偰摨偠傛偆偵夞揮偝偣偰傒傞偲丄妋偐偵撪岦偒偵壛懍搙乮岦怱椡乯傪惗偠傞偙偲偲側傞偑丄偦偺岦偒偑夞揮幉偵岦偐偭偰悅捈偵怢傃偰偍傜偢丄僷僱儖偺愜傝嬋偘曽岦偵偢傟偨岦偒傪巜偟偰偄傞丅 丂幚偼偙偙偑岆傝偱偁傝丄暔棟僔儈儏儗乕僔儑儞偲偟偰偺戞擇偺晄旛偱偁傞丅 丂偙偺応崌偺壛懍搙乮椡乯偼僷僱儖偺愜傝嬋偘妏搙偵娭傢傜偢丄夞揮幉偵懳偟偰悅捈側曽岦傪岦偄偰偄側偗傟偽僔儈儏儗乕僔儑儞偲偟偰惓妋偲偼尵偊側偄丅 丂偟偐偟暔棟墘嶼張棟傪幚憰偡傞偵摉偨偭偰丄彮偟偱傕張棟偺晧壸傪掅尭偝偣傞偨傔丄僷僱儖偵摥偔壛懍搙乮椡乯偺岦偒偼乮廳椡傪彍偄偰乯堦棩偵僷僱儖暯柺偐傜悅捈側岦偒偵摥偔傛偆偵丄張棟偑娵傔傜傟偨偺偩傠偆丅偁傞偄偼丄僷僱儖偵嶌梡偡傞椡偼廳椡偲嬻婥掞峈偺俀庬椶偺傒偲偟丄偦傟偧傟暿偺墘嶼傪梡偄偰僔儈儏儗乕僔儑儞傪峴偭偰偄傞偑丄岦怱椡偵娭偡傞墘嶼傪捛壛偡傞偩偗偺僷僼僅乕儅儞僗忋偺梋桾偑側偔丄巇曽側偔嬻婥掞峈偲摨偠張棟傪梡偄傞偙偲偵偟偨偺偩傠偆丅乮彮側偔偲傕廳椡偲摨偠張棟傪梡偄傞傛傝偼丄尰幚偵嬤偄傕偺偲側傞偩傠偆丅乯 丂偙傟偑寢壥偲偟偰丄僐乕儞儘乕僞偑梘椡傪敪惗偝偣傞儊僇僯僘儉偵側偭偰偄傞偲夝庍偡傞丅 丂嘆墦怱椡丄嘇岦怱椡偺岦偒乮儀僋僩儖乯丄彮側偔偲傕偙偺偳偪傜偐偑峫椂偝傟尰幚偺暔棟偵徠傜偟崌傢偝傟偨幚憰偑惉偝傟偰偄傟偽丄懄偪岦怱椡傗墦怱椡偲偄偭偨廳椡偲傕嬻婥掞峈偲傕堎側傞椡妛忋偺椡偵娭偡傞摿暿側僔儈儏儗乕僔儑儞偑偝傟偰偄傟偽丄偙偺傛偆側僷僱僉僢僩摿桳偺尰徾偼敪惗偟側偐偭偨傕偺偲巚傢傟傞丅 |
 |
|
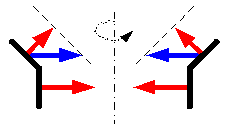
杮棃偼惵栴報偺傛偆側椡偑摥偔偑丄張棟傪娵傔偨寢壥丄愒栴報偺惉暘偺傒傪嵦梡偟偰偄傞壜擻惈偑偁傞丅 偦偺寢壥丄僷僱儖傪忋岦偵堷偒忋偘傞椡乮梘椡乯偑敪惗偟偰偟傑偭偰偄傞壜擻惈偑偁傞丅 |