<脳内ニューロン系とニューラルネットワークの起こり>
1.脳内神経細胞と人工ニューロン
1.1 ニューロンについて
人間の脳の中には、約 1,000 億個のニューロン(神経細胞)があり、それらが
信号伝達と発火(後述)を繰り返して様々な意識を生み出しています。
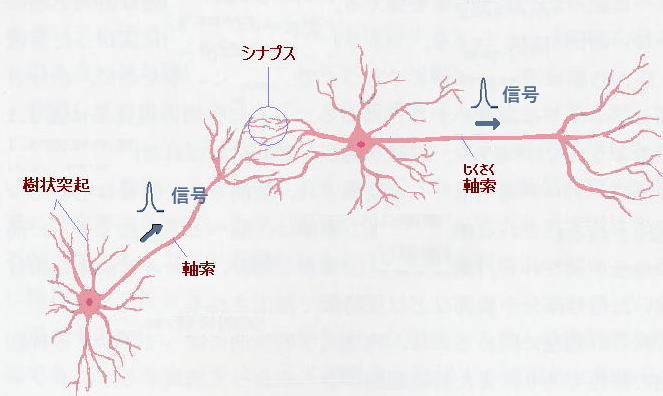
あるニューロンからは、発火の後、軸索を介してインパルス信号(パルス的な電圧)
を次のニューロンに伝えます。
ニューロン同士の信号の伝達は、上図のシナプス(狭い隙間)を介して行われます。
信号を受け取ったニューロンが発火すると、そのシナプスが強化されることが、ヘップ
によって実証されました。 これが、人間の学習や記憶の基本と見られています。
また、これは、人工知能での学習における重みの最適化とも関係しています。
次に発火について説明します。
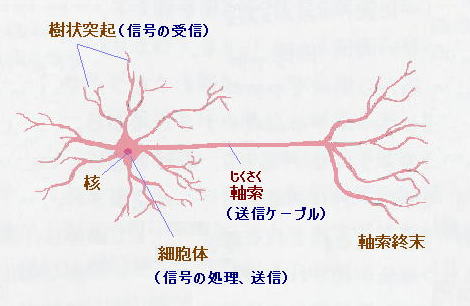
動物や人間では、いくつかの樹状突起に信号が入力すると、それらの合計として、
細胞体の中の電圧が上昇します。
細胞体内の電圧(細胞外との電位差)がある値Vo までは、そのニューロンには何の
変化も起こりません。 しかし、電圧がVo を超えた瞬間、ニューロンは突然、癇癪玉を
破裂させたかのように、瞬間的に高い電圧を発生させ、軸索を介して次のニューロンに
そのインパルスを伝えます。 これをニューロンの発火と言います。
(この発火こそが、我々の意識発生の発端、と考えていますが。)
人工知能では、このニューロンの発火現象を、数学的に下図のような関数で表現し
ます。 両者とも、活性化関数と呼ばれます。
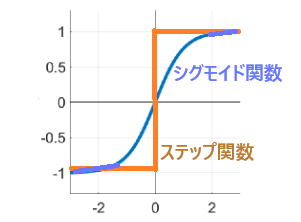
人工知能研究の初期には、活性化関数として、グラフ内オレンジ色のステップ関数が
用いられました。 その後、学習において、誤差を修正する必要上、滑らかな(青色の)
シグモイド関数等が使われるようになりました。 (原点の取り方は任意)
1.2 ニューロンを模した形式ニューロンとパーセプトロン
<形式ニューロン>
人工知能の発端としては、下図に示すような形式ニューロンがあります。
これは、1943年にウォーレン・マカロックとウォルター・ピッツが発表したもので、神経
細胞の発火挙動を数理モデル化したものです。
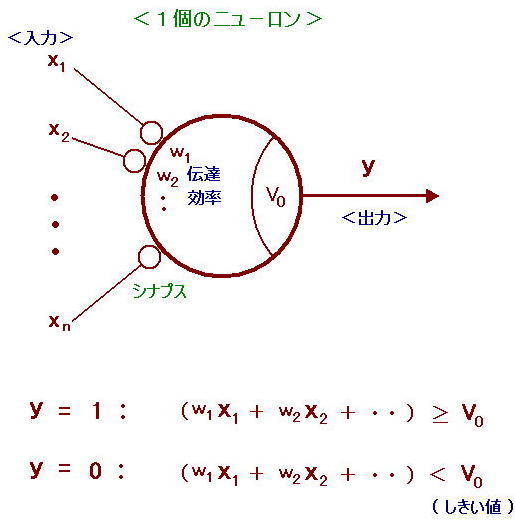
ここでは、入力 x に重み w をかけた値が、中央円形のニューロンに入り込んで、合計
され、内部の値(電圧に対応)がある値 Vo に達したら、y に 出力 1 を発信出力する、と
いうものです。
( Voに達するまでは、出力 0 です。 簡単の為、バイアスは省略しました。)
この後、1949年にHebb が学習則を発表します。
<パーセプトロン>
この形式ニューロンの考え方をより発展させたのが、1958年にローゼンブラッドが考案
したパーセプトロンモデルです。
ローゼンブラッドのパーセプトロンモデルは、人間の視覚と脳の機能をモデル
化したもので、パターン認識を行うためのものです。
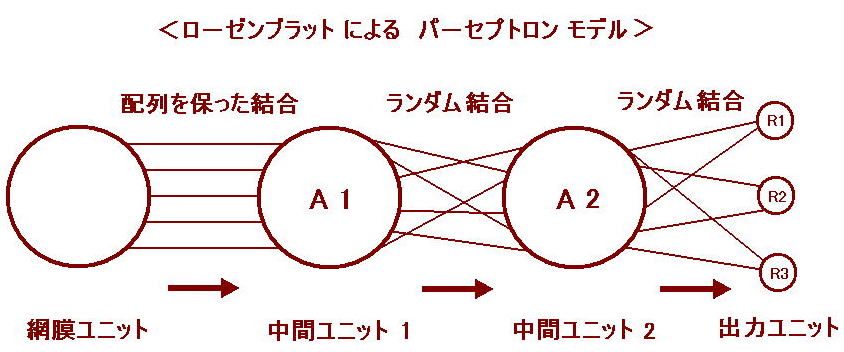
これは、S層(感覚層、入力層)、A層(連合層、中間層)、R層(反応層、出力層)の
3種類の部分からなります。
中間層のA1層とA2層の間、及びA2層とR層の間はランダムに接続されています。
S層(網膜ユニット)には外部から信号が与えられます。
このモデルは、S層とA1層が配列を保った結合なので、数学的には同一の層とみなす
ことができ、本質的に3層パーセプトロンとみなされます。
A2層はA1層からの情報を元に反応します。 R層はA2層からの伝達値に重みづけをし
た上で積算し、R層の間で、多数決によって答えを出します。
ローゼンブラットは、課題ごとにこの重み(結合強度)をどう学習させれば良いのかに
ついて「パーセプトロンの学習則」 にまとめました。
また、パーセプトロンの計算を実行するために、彼自身が、次のような電子装置を作成
しました。

Mark I パーセプトロン
このマシンは、20×20 個の光を電気に変換する装置(カメラ)を備えており、合計で
400ピクセルの画像を入力として扱うことができました。 入力データのさまざまな組み合
わせを設定するためのパッチパネルがあります。
ローゼンブラットのパーセプトロンモデルは、3層パーセプトロンですが、中間層から
出力層までの経路の重みを、学習の過程でどのようにして最適化すべきか、方法が
確立されてなかったため、初期に研究されたのは、単純パーセプトロンでした。
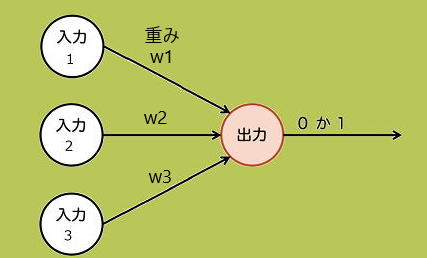
単純パーセプトロン(2層パーセプトロン)は、二項分類問題(二つのカテゴリーに
データを分ける問題)を対象としています。
パーセプトロンは、脳のニューロンを数学的にモデル化したものですが、それ以降
発展したニューラルネットワークの出発点としての意義があります。
ニューラルネットワークの学習は、正しい答えを出せるようにように、重みを修正していく
というプロセスになります。
ミンスキー とパパートは、下図のようなモデルに基づいて、二項分類問題に取り
組みました。 (これは、2層パーセプトロンです。)
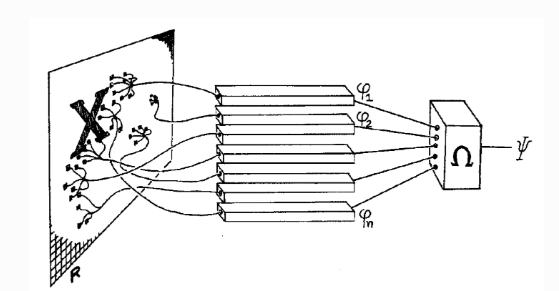
(パーセプトロンの模式図(ミンスキー & パパート)
しかしながら、この単純パーセプトロンは、下図左のように、境界が直線になる
ようなグループの仕分けはできても、下図右のように、境界線が曲線になるような
グループの仕分けは不可能であることが判明しました。
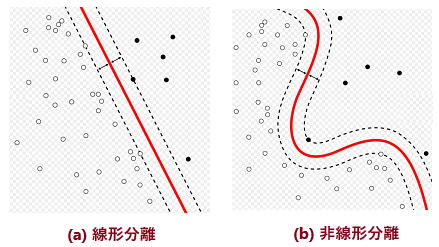
そのため、その後の人工知能研究は、冬の時代に入りました。
1.3 多層パーセプトロンと、勾配降下法及び逆誤差伝播法
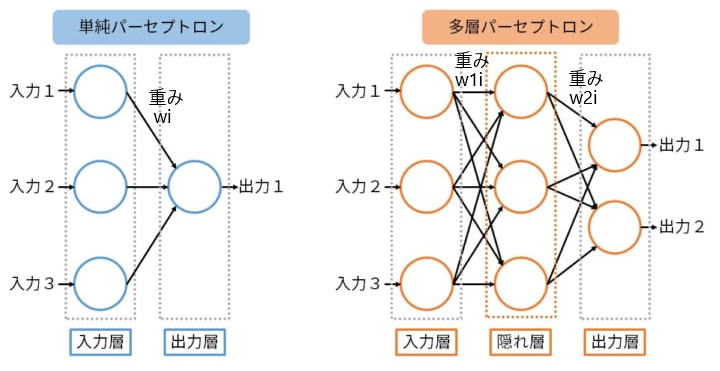
1980年代からは、上図右のように、入力層と出力層の間に隠れ層(中間層)を
挿入した多層パーセプトロンの研究が盛んになり、非線形分離問題も解けるようになり
ました。
<勾配降下法>
まずは3層パーセプトロンが研究されましたが、重み最適化の計算には、次のような
勾配降下法が用いられました。
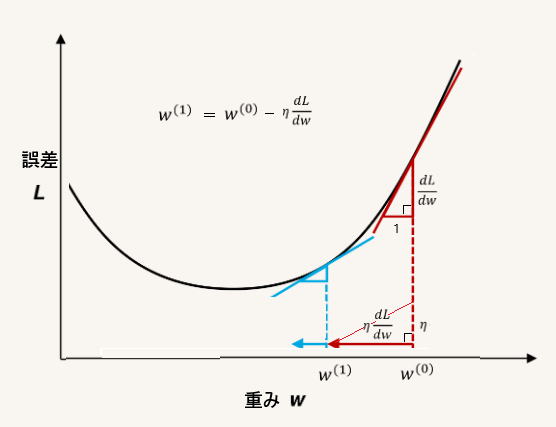
上のグラフは、誤差L(出力と正解データの差)と重みW の関係を示したものです。
(もちろん、重みパラメータは複数ですが、イメージしやすいように、1軸だけで表して
います。)
通常、ηは、1 以下の定数が用いられています。
目標は誤差L を最小にするような重み(の数列)W を求めることですが、グラフに
示した数式の計算を繰り返すことによって、赤 → 青 と次第に曲線の底辺に近づいて
いくことがわかります。
誤差L が最小の時は、勾配がゼロなので、数式の第2項はゼロとなり、Wはそこの
値に収束します。
<誤差逆伝播法>
中間層が1層かそれ以上あるものは、一般にニューラルネットワーク(NN)と呼ばれ
ます。
NN(ニューラルネットワーク)の学習において、重みを最適化する(正解を出せるよう
に学習する)方法としては、勾配降下法と共に、次のような誤差逆伝播法が用いられ
ます。
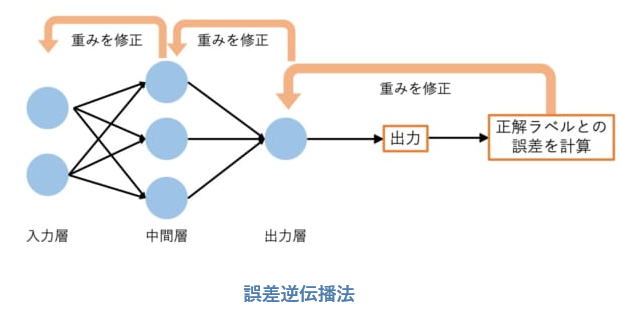
誤差逆伝播法とは、誤差L を最小にすべく、重みを後ろ側(出力側)から順に修正して
いく方法です。
数学的には、勾配降下法と連鎖律の組み合わせで計算します。
連鎖律とは、次のように、合成関数の微分が、2段階の微分の積になることです。

そもそも、誤差とは、出力と正解データとの差なので、修正(重みの変更)は出力側から
やっていかざるを得ないのは、当然ですね。
本格的な誤差逆伝播法は、1986年にアメリカの心理学者デビッド・ラメルハートらに
よって公開されましたが、それによって、第2次AIブームが起こりました。
しかしながら、多層化の際の勾配消失問題や学習データ不足等のため、1995年頃には、
再びブームが下火になりました。 勾配消失問題に関しては、DNNのページで述べます。