この文書はRFC1750の日本語訳(和訳)です。
この文書の翻訳内容の正確さは保障できないため、
正確な知識を求める方は原文を参照してください。
翻訳者はこの文書によって読者が被り得る如何なる損害の責任をも負いません。
この翻訳内容に誤りがある場合、訂正版の公開や、
誤りの指摘は適切です。
この文書の配布は元のRFC同様に無制限です。
※コピーする際はイメージファイルのコピーも忘れずに
Network Working Group D. Eastlake, 3rd
Request for Comments: 1750 DEC
Category: Informational S. Crocker
Cybercash
J. Schiller
MIT
December 1994
Randomness Recommendations for Security
セキュリティのためのランダムさの推薦
Status of this Memo
この文書の状態
This memo provides information for the Internet community. This memo
does not specify an Internet standard of any kind. Distribution of
this memo is unlimited.
このメモはインターネット共同体のための情報を供給します。これはいかな
るインターネット標準も指定しません。このメモの配布は無制限です。
Abstract
概要
Security systems today are built on increasingly strong cryptographic
algorithms that foil pattern analysis attempts. However, the security
of these systems is dependent on generating secret quantities for
passwords, cryptographic keys, and similar quantities. The use of
pseudo-random processes to generate secret quantities can result in
pseudo-security. The sophisticated attacker of these security
systems may find it easier to reproduce the environment that produced
the secret quantities, searching the resulting small set of
possibilities, than to locate the quantities in the whole of the
number space.
今日のセキュリティシステムがホイルパターン分析を試す、ますます強い暗
号のアルゴリズムの上に構築されます。しかしながら、これらのシステムの
安全管理はパスワードや暗号カギや類似の秘密の値を生成することに依存し
ています。秘密の値を生成する疑似ランダムプロセスの使用は疑似セキュリ
ティをもたらすことができます。これらのセキュリティシステムの精巧な攻
撃者は、数値空間の全体の中から数値を突き止めるより、秘密を生成した環
境を再現し、結果として生じている可能性のある小さい集合を捜索する方が、
より容易であることを見つけるかもしれません。
Choosing random quantities to foil a resourceful and motivated
adversary is surprisingly difficult. This paper points out many
pitfalls in using traditional pseudo-random number generation
techniques for choosing such quantities. It recommends the use of
truly random hardware techniques and shows that the existing hardware
on many systems can be used for this purpose. It provides
suggestions to ameliorate the problem when a hardware solution is not
available. And it gives examples of how large such quantities need
to be for some particular applications.
ランダムな値を、臨機応変でやる気満々の敵に失敗させるように選ぶことは
驚くほど難しいです。この文書はこのような値を選択することに対して伝統
的な疑似乱数生成テクニックの多くの落とし穴を指摘します。これは本当に
ランダムなハードウェアテクニックの使用を勧め、多くのシステムの上の既
存のハードウェアがこの目的のために使われることができることを示します。
これは、ハードウェア解決が利用可能ではない時、問題を改善するために提
案を供給します。そしてこれは、このような値がある特定のアプリケーショ
ンのためにどれぐらい大きく必要かについて、例を与えます。
Acknowledgements
謝辞
Comments on this document that have been incorporated were received
from (in alphabetic order) the following:
この文書に含まれるコメントは以下の方から受取りました(アルファベット順):
David M. Balenson (TIS)
Don Coppersmith (IBM)
Don T. Davis (consultant)
Carl Ellison (Stratus)
Marc Horowitz (MIT)
Christian Huitema (INRIA)
Charlie Kaufman (IRIS)
Steve Kent (BBN)
Hal Murray (DEC)
Neil Haller (Bellcore)
Richard Pitkin (DEC)
Tim Redmond (TIS)
Doug Tygar (CMU)
Table of Contents
目次
1. Introduction
1. はじめに
2. Requirements
2. 必要条件
3. Traditional Pseudo-Random Sequences
3. 伝統的疑似ランダム列
4. Unpredictability
4. 予知不可能さ
4.1 Problems with Clocks and Serial Numbers
4.1 時計における問題と通し番号
4.2 Timing and Content of External Events
4.2 タイミングと外部イベントの内容
4.3 The Fallacy of Complex Manipulation
4.3 複雑な扱いの誤った推理
4.4 The Fallacy of Selection from a Large Database
4.4 大きいデータベースからの選択の誤り
5. Hardware for Randomness
5. ハードウェアの乱雑さ
5.1 Volume Required
5.1 必要な量
5.2 Sensitivity to Skew
5.2 ゆがみに対する敏感さ
5.2.1 Using Stream Parity to De-Skew
5.2.1 ゆがみを直すために流れのパリティを使う
5.2.2 Using Transition Mappings to De-Skew
5.2.2 歪みを直す翻訳マッピングの使用
5.2.3 Using FFT to De-Skew
5.2.3 歪みを直すFFTの使用
5.2.4 Using Compression to De-Skew
5.2.4 歪みを直す圧縮の使用
5.3 Existing Hardware Can Be Used For Randomness
5.3 の既存ハードウェアが乱雑さに使えます
5.3.1 Using Existing Sound/Video Input
5.3.1 既存の音声/ビデオ入力の使用
5.3.2 Using Existing Disk Drives
5.3.2 既存ディスク・ドライブを使う
6. Recommended Non-Hardware Strategy
6. 推薦された非ハードウェアの戦略
6.1 Mixing Functions
6.1 混合関数
6.1.1 A Trivial Mixing Function
6.1.1 つまらない混合関数
6.1.2 Stronger Mixing Functions
6.1.2 強力な混合関数
6.1.3 Diffie-Hellman as a Mixing Function
6.1.3 混合関数としてのDiffie-Hellman
6.1.4 Using a Mixing Function to Stretch Random Bits
6.1.4 ランダムビットを拡張するための混合関数の使用
6.1.5 Other Factors in Choosing a Mixing Function
6.1.5 混合関数を選択する他の要因
6.2 Non-Hardware Sources of Randomness
6.2 乱雑の非ハードウェアソース
6.3 Cryptographically Strong Sequences
6.3 暗号的に強い列
6.3.1 Traditional Strong Sequences
6.3.1 伝統的な強い列
6.3.2 The Blum Blum Shub Sequence Generator
6.3.2 Blum Blum Shub列生成機
7. Key Generation Standards
7. 鍵生成標準
7.1 US DoD Recommendations for Password Generation
7.1 パスワード生成の合衆国DoD推薦
7.2 X9.17 Key Generation
7.2 X9.17鍵生成
8. Examples of Randomness Required
8. 必要な乱雑さの例
8.1 Password Generation
8.1 パスワード生成
8.2 A Very High Security Cryptographic Key
8.2 非常に高セキュリティの暗号鍵
8.2.1 Effort per Key Trial
8.2.1 鍵判定毎の努力
8.2.2 Meet in the Middle Attacks
8.2.2 中間一致攻撃
8.2.3 Other Considerations
8.2.3 他の考慮
9. Conclusion
9. 結論
10. Security Considerations
10. セキュリティの考察
References
参考文献
Authors' Addresses
著者のアドレス
1. Introduction
1. はじめに
Software cryptography is coming into wider use. Systems like
Kerberos, PEM, PGP, etc. are maturing and becoming a part of the
network landscape [PEM]. These systems provide substantial
protection against snooping and spoofing. However, there is a
potential flaw. At the heart of all cryptographic systems is the
generation of secret, unguessable (i.e., random) numbers.
ソフトウェア暗号がより広い使用にかかわっています。Kerberos、PEM、PGP
などのようなシステムが成熟して、ネットワークの風景の一部になっていま
す[PEM]。これらのシステムは詮索と詐欺に対しての相当な保護を供給します。
しかし、可能性がある傷があります。すべての暗号のシステムの心臓は秘密
鍵、予想できない(つまりランダムな)数の生成です。
For the present, the lack of generally available facilities for
generating such unpredictable numbers is an open wound in the design
of cryptographic software. For the software developer who wants to
build a key or password generation procedure that runs on a wide
range of hardware, the only safe strategy so far has been to force
the local installation to supply a suitable routine to generate
random numbers. To say the least, this is an awkward, error-prone
and unpalatable solution.
当分、このような予想できない数を生成するための一般に利用可能な機能の
欠如は暗号のソフトウェアのデザインのオープンな傷です。広範囲のハード
ウェアで動作する鍵やパスワード生成手順を望むソフトウェア開発業者のた
めに、唯一の安全な戦略はこれまでのところ乱数を生成するために適当なルー
チンのローカルな導入でした。控えめに言っても、これはぐあいが悪く、エ
ラーの傾向があり、口当たりが悪い解決です。
It is important to keep in mind that the requirement is for data that
an adversary has a very low probability of guessing or determining.
This will fail if pseudo-random data is used which only meets
traditional statistical tests for randomness or which is based on
limited range sources, such as clocks. Frequently such random
quantities are determinable by an adversary searching through an
embarrassingly small space of possibilities.
敵がデータを推測するか決定しできる確率が非常に低いという必要条件を念
頭におくことは重要です。これは、もしただ乱雑さが伝統的な統計テストを
満たすだけで、時計のような限定されたソースに基づいている疑似ランダム
なデータが使われるなら、失敗するでしょう。しばしばこのような乱数は、
とても小さい数値空間を捜している敵にとって決定可能です。
This informational document suggests techniques for producing random
quantities that will be resistant to such attack. It recommends that
future systems include hardware random number generation or provide
access to existing hardware that can be used for this purpose. It
suggests methods for use if such hardware is not available. And it
gives some estimates of the number of random bits required for sample
applications.
この情報的な文書はこのような攻撃に対して抵抗力があるであろうランダム
量を作り出すテクニックを示唆します。これは未来のシステムがハードウェ
ア乱数生成を含むか、あるいはこの目的のために使える既存のハードウェア
へのアクセスを供給することを勧めます。もしこのようなハードウェアが利
用可能ではない場合の、使用できる方法を示唆します。そしてあるサンプル
アプリケーションで必要なランダムビット数の見積もりを与えます。
2. Requirements
2. 必要条件
Probably the most commonly encountered randomness requirement today
is the user password. This is usually a simple character string.
Obviously, if a password can be guessed, it does not provide
security. (For re-usable passwords, it is desirable that users be
able to remember the password. This may make it advisable to use
pronounceable character strings or phrases composed on ordinary
words. But this only affects the format of the password information,
not the requirement that the password be very hard to guess.)
恐らく今日最も一般に遭遇される乱雑が必要な状況はユーザーパスワードで
す。これは通常単純な文字列です。明らかに、もしパスワードが推測できる
なら、パスワードはセキュリティを供給しません。(再利用可能なパスワー
ドのために、ユーザーがパスワードを覚えることが可能であることが望まし
いです。これは発音可能な文字列、あるいは普通の単語から構成された文を
使うことが賢明かもしれません。けれどもこれはただ、パスワードが推測す
ることが非常に難しいという必要事項ではなく、パスワード情報のフォーマッ
トに影響を与えるだけです。)
Many other requirements come from the cryptographic arena.
Cryptographic techniques can be used to provide a variety of services
including confidentiality and authentication. Such services are
based on quantities, traditionally called "keys", that are unknown to
and unguessable by an adversary.
多くの他の必要条件が暗号の舞台から来ます。暗号の技術が機密性と認証を
含めていろいろなサービスを供給するために使うことができます。このよう
なサービスは、伝統的に「鍵」と呼ばれる、敵に未知で推測できない数に基
づいています。
In some cases, such as the use of symmetric encryption with the one
time pads [CRYPTO*] or the US Data Encryption Standard [DES], the
parties who wish to communicate confidentially and/or with
authentication must all know the same secret key. In other cases,
using what are called asymmetric or "public key" cryptographic
techniques, keys come in pairs. One key of the pair is private and
must be kept secret by one party, the other is public and can be
published to the world. It is computationally infeasible to
determine the private key from the public key [ASYMMETRIC, CRYPTO*].
ある場合、ワンタイムパスワード[CRYPTO*]や合衆国データ暗号化規格[DES]
にような、暗号化と認証のある通信を求めるグループが共通秘密鍵を知って
なければなりません。他の場合、非対称または「公開鍵」暗号と呼ばれる技
術を使い、鍵の対を使います。鍵の対の1つはプライベートで、一方のグルー
プが秘密にしておかなければなりません、他方は公開であり世界に報知でき
ます。公開鍵から秘密鍵を決定するのは計算量的に不可能です[ASYMMETRIC,
CRYPTO*]。
The frequency and volume of the requirement for random quantities
differs greatly for different cryptographic systems. Using pure RSA
[CRYPTO*], random quantities are required when the key pair is
generated, but thereafter any number of messages can be signed
without any further need for randomness. The public key Digital
Signature Algorithm that has been proposed by the US National
Institute of Standards and Technology (NIST) requires good random
numbers for each signature. And encrypting with a one time pad, in
principle the strongest possible encryption technique, requires a
volume of randomness equal to all the messages to be processed.
乱数の必要な頻度と量は暗号システム毎に大いに異なります。純粋なRAS
[CRYPTO*]を使う場合、乱数は鍵対が生成される時に必要で、その後はそれ
以上の乱数なしでどんなメッセージでも署名できます。米国政府標準技術局
(NIST)によって提言された公開鍵ディジタル署名アルゴリズムは各署名に良
い乱数を必要とします。そしてワンタイムパッドの暗号化は、原則として最
も強い可能な暗号化技術と、処理されるすべてのメッセージと等しい量の乱
数を要求します。
In most of these cases, an adversary can try to determine the
"secret" key by trial and error. (This is possible as long as the
key is enough smaller than the message that the correct key can be
uniquely identified.) The probability of an adversary succeeding at
this must be made acceptably low, depending on the particular
application. The size of the space the adversary must search is
related to the amount of key "information" present in the information
theoretic sense [SHANNON]. This depends on the number of different
secret values possible and the probability of each value as follows:
これらのケースの大部分で、敵が試行錯誤によって「秘密」鍵を決定しよう
とすることができます。(これは、正しい鍵がユニークに識別できるぐらい
メッセージより鍵が小さい限り、可能です。)アプリケーション依存で、こ
れに成功する敵のいる確率が十分低くなければなりません。敵が検索しなく
てはならない空間の大きさは情報理論的な意味で存在している鍵の「情報」
量と関係があります[SHANNON]。これは次のように可能な異なる秘密値と各
値の確率に頼ります:
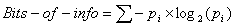
where i varies from 1 to the number of possible secret values and p
sub i is the probability of the value numbered i. (Since p sub i is
less than one, the log will be negative so each term in the sum will
be non-negative.)
ここで変数iが1から可能な秘密値の数を取り、下付きのiを添えたpがi
番目の確率です。(下付きのiを添えたpは1以下で、logは負の値になり、
各項の合計は正の値になります)。
If there are 2^n different values of equal probability, then n bits
of information are present and an adversary would, on the average,
have to try half of the values, or 2^(n-1) , before guessing the
secret quantity. If the probability of different values is unequal,
then there is less information present and fewer guesses will, on
average, be required by an adversary. In particular, any values that
the adversary can know are impossible, or are of low probability, can
be initially ignored by an adversary, who will search through the
more probable values first.
もし2^nの異なる値が等しい確率なら、nビットの情報があり、敵が秘密の
量を推測するのに平均して2^(n−1)回の試行をする必要があります。
もし異なる値の確率が等しくないなら、より少ない情報が存在し、平均的に
的が必要な推測はより少ないでしょう。特に、敵がありえない値や可能性の
低い値を知っていれば、初めに可能性の高い値を探す敵はそれらを無視でき
ます。
For example, consider a cryptographic system that uses 56 bit keys.
If these 56 bit keys are derived by using a fixed pseudo-random
number generator that is seeded with an 8 bit seed, then an adversary
needs to search through only 256 keys (by running the pseudo-random
number generator with every possible seed), not the 2^56 keys that
may at first appear to be the case. Only 8 bits of "information" are
in these 56 bit keys.
例えば、56ビット鍵を使う暗号のシステムを考えてください。もし56ビッ
トの鍵が8ビットの種の擬似乱数生成機で作られるなら、敵は256個の鍵
を探すだけで済みます(すべての可能な種を元に疑似乱数生成機を動かすこ
とによって)、この場合2^56種類の鍵が最初に発生しません。これらの
56ビット鍵の情報は8ビットだけです。
3. Traditional Pseudo-Random Sequences
3. 伝統的疑似ランダム列
Most traditional sources of random numbers use deterministic sources
of "pseudo-random" numbers. These typically start with a "seed"
quantity and use numeric or logical operations to produce a sequence
of values.
たいていの伝統的な乱数情報源が決定情報源の「疑似ランダム」数を使いま
す。これらは典型的に「種」数から始まり、数値列を作り出すために数値演
算か論理演算を使います。
[KNUTH] has a classic exposition on pseudo-random numbers.
Applications he mentions are simulation of natural phenomena,
sampling, numerical analysis, testing computer programs, decision
making, and games. None of these have the same characteristics as
the sort of security uses we are talking about. Only in the last two
could there be an adversary trying to find the random quantity.
However, in these cases, the adversary normally has only a single
chance to use a guessed value. In guessing passwords or attempting
to break an encryption scheme, the adversary normally has many,
perhaps unlimited, chances at guessing the correct value and should
be assumed to be aided by a computer.
[KNUTH]は疑似乱数の古典的な一覧を示します。彼が述べるアプリケーション
は、自然の現象のシュミレーション、サンプリング、数値分析、テストコン
ピュータ・プログラム、決断、ゲームです。これらのいずれも今話をしてい
るセキュリティと同じ特徴を持ちません。最後の2つだけが乱数を発見しよ
うとする敵があり得ます。しかしながら、これらの場合、敵は通常ただ推測
された値を使うチャンスが1回だけです。パスワード推測や暗号破壊を試み
る敵は、通常何度も、多分無限に正しい値を推測するチャンスがあり、コン
ピュータの援助があると考えられます。
For testing the "randomness" of numbers, Knuth suggests a variety of
measures including statistical and spectral. These tests check
things like autocorrelation between different parts of a "random"
sequence or distribution of its values. They could be met by a
constant stored random sequence, such as the "random" sequence
printed in the CRC Standard Mathematical Tables [CRC].
数の「乱雑度」のテストに対して、Knuthはいろいろな統計的な、そして奇怪
な尺度を提案しています。これらのテストは「ランダム」列の異なる部分の
自動相関や分散の検査をします。これらは、 CRC標準数表[CRC]で印刷さ
れた「ランダム」列のような、不変の記憶されたランダム列によって実施で
きます。
A typical pseudo-random number generation technique, known as a
linear congruence pseudo-random number generator, is modular
arithmetic where the N+1th value is calculated from the Nth value by
線形一致疑似乱数生成機として知られる典型的な疑似乱数の生成テクニック
が、以下の様にN番目の値からN+1番目の値を計算するモジュール演算で
す。
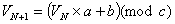
The above technique has a strong relationship to linear shift
register pseudo-random number generators, which are well understood
cryptographically [SHIFT*]. In such generators bits are introduced
at one end of a shift register as the Exclusive Or (binary sum
without carry) of bits from selected fixed taps into the register.
上記のテクニックは暗号的によく理解されている線形シフトレジスタ疑似乱
数生成機との強い関連を持っています[SHIFT*]。このような生成機で、あら
かじめ選択されているレジスタの固定タップの排他的論理和(キャリアなし
の2進数加算)の結果のビットがレジスタの一方の端に挿入されます。
For example:
例えば:
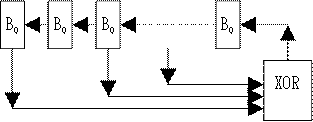
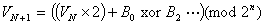
The goodness of traditional pseudo-random number generator algorithms
is measured by statistical tests on such sequences. Carefully chosen
values of the initial V and a, b, and c or the placement of shift
register tap in the above simple processes can produce excellent
statistics.
伝統的な疑似乱数生成機のアルゴリズムの良さはこのような列上での統計テ
ストによって測られます。慎重に最初のVとaとbとcの値を選択するか、
Vと上記の単純なプロセスのシフトレジスタのタップ位置を選択すると、統
計的に優秀なものを作り出せます。
These sequences may be adequate in simulations (Monte Carlo
experiments) as long as the sequence is orthogonal to the structure
of the space being explored. Even there, subtle patterns may cause
problems. However, such sequences are clearly bad for use in
security applications. They are fully predictable if the initial
state is known. Depending on the form of the pseudo-random number
generator, the sequence may be determinable from observation of a
short portion of the sequence [CRYPTO*, STERN]. For example, with
the generators above, one can determine V(n+1) given knowledge of
V(n). In fact, it has been shown that with these techniques, even if
only one bit of the pseudo-random values is released, the seed can be
determined from short sequences.
これらの数列は、数列が調査している空間構造に無関係である限り、シミュ
レーション(モンテカルロ実験)で適切かもしれません。それでも、敏感な
パターンが問題を起こすかもしれません。しかしながら、このような数列は
セキュリティアプリケーションで明らかに良くありません。数列は、最初の
状態が知られているなら、完全に予測可能です。疑似乱数生成機の形式に依
存して、数列は数列の短い部分の観察からの決定できるかもしれません
[CRYPTO*, STERN]。例えば、上記生成機は、V(n)を知っている人はV(n+1)を
決定できます。実際に、これらのテクニックで、たとえ擬似乱数値のたった
1ビットだけ公表されてるとしても、短い数列から種が決意できる事が明ら
かにされました。
Not only have linear congruent generators been broken, but techniques
are now known for breaking all polynomial congruent generators
[KRAWCZYK].
単に線形合同生成機が問題なだけではなく、すべての多項式合同生成機が問
題あるのが周知です[KRAWCZYK]。
4. Unpredictability
4. 予知不可能さ
Randomness in the traditional sense described in section 3 is NOT the
same as the unpredictability required for security use.
3章で記述された伝統的な意味での乱数はセキュリティで使用できるほど予
知不可能ではありません。
For example, use of a widely available constant sequence, such as
that from the CRC tables, is very weak against an adversary. Once
they learn of or guess it, they can easily break all security, future
and past, based on the sequence [CRC]. Yet the statistical
properties of these tables are good.
例えば、CRC表のような、広く利用可能な定数列の使用は敵に対して非常
に弱いです。敵がそれを知るか推測した途端に、数列[CRC]に基づいて容易に
未来と過去のすべてのセキュリティを破壊できます。それでもこれらの表の
統計上の特性は良いです。
The following sections describe the limitations of some randomness
generation techniques and sources.
次の章はある乱数生成テクニックとソースの限界を記述します。
4.1 Problems with Clocks and Serial Numbers
4.1 時計における問題と通し番号
Computer clocks, or similar operating system or hardware values,
provide significantly fewer real bits of unpredictability than might
appear from their specifications.
コンピュータ時計が、オペレーティング・システムやハードウェア値も、予
知不可能さについては仕様書に記述される範囲より本当は少ないビット数を
供給します。
Tests have been done on clocks on numerous systems and it was found
that their behavior can vary widely and in unexpected ways. One
version of an operating system running on one set of hardware may
actually provide, say, microsecond resolution in a clock while a
different configuration of the "same" system may always provide the
same lower bits and only count in the upper bits at much lower
resolution. This means that successive reads on the clock may
produce identical values even if enough time has passed that the
value "should" change based on the nominal clock resolution. There
are also cases where frequently reading a clock can produce
artificial sequential values because of extra code that checks for
the clock being unchanged between two reads and increases it by one!
Designing portable application code to generate unpredictable numbers
based on such system clocks is particularly challenging because the
system designer does not always know the properties of the system
clocks that the code will execute on.
テストが多数のシステムの上に時計でされ、それらの動作が広く意外な方法
で変化することが気付かれました。いくつものハードウェア上で動作するオ
ペレーティング・システムのあるバージョンがマイクロセカンドの精度の時
計を供給できるが、「同じ」システムの異なった設定で低位ビットが常に同
じで、上位ビットだけをカウントするよろ低い精度です。これは、たとえ名
目上の時計の精度に基づくと値が変化している「べきである」十分な時間が
過ぎ去ったとしても、時計の連続した読み出しが同一の値を作り出すかもし
れないことを意味します。同じく連続した時計の読みこみで2つの読み取り
の間に時計が変化していないと値を1つ増加させる余計なコードによって人
工的な連続値を作り出す場合があります!このようなシステム時計に基づい
て予想できない数を生成する持ち運び可能なアプリケーションコードを設計
することは、システムデザイナーが常にコードを実行するシステム時計の特
性を知っているわけではないから、特に危険です。
Use of a hardware serial number such as an Ethernet address may also
provide fewer bits of uniqueness than one would guess. Such
quantities are usually heavily structured and subfields may have only
a limited range of possible values or values easily guessable based
on approximate date of manufacture or other data. For example, it is
likely that most of the Ethernet cards installed on Digital Equipment
Corporation (DEC) hardware within DEC were manufactured by DEC
itself, which significantly limits the range of built in addresses.
イーサネットアドレスのようなハードウェアの通し番号の使用は同じく思っ
たより少ないユニークさのビットを供給するかもしれません。このような数
は通常かなり構造化されていて、サブフィールドで可能な値が限定された範
囲にあるか、容易におよその製造日あるいは他のデータに基づいて推測でき
るかもしれません。例えば、デジタル・イクイップメント株式会社(DEC)
ハードウェアの上にインストールしたイーサネットカードの大部分がDEC
自身によって生産されたことはありそうで、これは組み込みのアドレスの範
囲を制限します。
Problems such as those described above related to clocks and serial
numbers make code to produce unpredictable quantities difficult if
the code is to be ported across a variety of computer platforms and
systems.
時計と通し番号に関係がある上記のような問題は、もしコードがいろいろな
コンピュータプラットホームとシステムで使われるなら、予想できない数を
作り出すコードを作るのを難しくします。
4.2 Timing and Content of External Events
4.2 タイミングと外部イベントの内容
It is possible to measure the timing and content of mouse movement,
key strokes, and similar user events. This is a reasonable source of
unguessable data with some qualifications. On some machines, inputs
such as key strokes are buffered. Even though the user's inter-
keystroke timing may have sufficient variation and unpredictability,
there might not be an easy way to access that variation. Another
problem is that no standard method exists to sample timing details.
This makes it hard to build standard software intended for
distribution to a large range of machines based on this technique.
マウスの動き、キーストロークと類似のユーザーイベントのタイミングと内
容を評価することは可能です。これはある量の予測できないデータの合理的
な情報源です。ある機械で、キーストロークのような入力がバッファされま
す。ユーザーのキーストローク間のタイミングが十分な変化と予知不可能さ
を持つかもしれないが、その変化にアクセスする容易な方法がないかもしれ
ません。もう1つの問題はタイミングの詳細を得る標準的方法が存在しない
ということです。これはこのテクニックに基づいた多くのマシンへ配布を意
図した標準ソフトウェアの構築を難しくします。
The amount of mouse movement or the keys actually hit are usually
easier to access than timings but may yield less unpredictability as
the user may provide highly repetitive input.
マウスの動きの量や実際に打たれたキーは通常タイミングよりアクセスが容
易ですが、ユーザーが反復的な入力を供給できるので、予測不能さが少ない
かもしれません。
Other external events, such as network packet arrival times, can also
be used with care. In particular, the possibility of manipulation of
such times by an adversary must be considered.
ネットワークパケット到着時刻のような、他の外部イベントも同じく注意し
て使うことができます。特に、敵がこのような時刻を扱える可能性を考慮し
なくてはなりません。
4.3 The Fallacy of Complex Manipulation
4.3 複雑な扱いの誤った推理
One strategy which may give a misleading appearance of
unpredictability is to take a very complex algorithm (or an excellent
traditional pseudo-random number generator with good statistical
properties) and calculate a cryptographic key by starting with the
current value of a computer system clock as the seed. An adversary
who knew roughly when the generator was started would have a
relatively small number of seed values to test as they would know
likely values of the system clock. Large numbers of pseudo-random
bits could be generated but the search space an adversary would need
to check could be quite small.
予知不可能さの紛らわしい出演を与えるかもしれないある戦略が非常に複雑
なアルゴリズム(あるいは良い統計上の特性を持つ優秀な伝統的な疑似乱数
生成機)を使って、種としてコンピュータシステム時計の現在の値で開始す
る暗号鍵計算です。およそいつ生成機が起動したか知っている敵が、システ
ム時計のありそうな値を知るであろうから、テストをする必要な種は比較的
少ないでしょう。多数の疑似ランダムなビットが生成できますが、敵がチェッ
クする必要がある捜索空間は非常に小さいです。
Thus very strong and/or complex manipulation of data will not help if
the adversary can learn what the manipulation is and there is not
enough unpredictability in the starting seed value. Even if they can
not learn what the manipulation is, they may be able to use the
limited number of results stemming from a limited number of seed
values to defeat security.
それで、もし敵が扱いが何か学ぶことができ最初の種の値に十分な予測不可
能さがないなら、データの非常に強力で複雑な扱いは助けにならないでしょ
う。たとえ的が扱いが何かを学ぶことができないとしても、それらの結果の
限定された数が種の値を限定しセキュリティを破ることが可能かもしれませ
ん。
Another serious strategy error is to assume that a very complex
pseudo-random number generation algorithm will produce strong random
numbers when there has been no theory behind or analysis of the
algorithm. There is a excellent example of this fallacy right near
the beginning of chapter 3 in [KNUTH] where the author describes a
complex algorithm. It was intended that the machine language program
corresponding to the algorithm would be so complicated that a person
trying to read the code without comments wouldn't know what the
program was doing. Unfortunately, actual use of this algorithm
showed that it almost immediately converged to a single repeated
value in one case and a small cycle of values in another case.
もう1つの重大な戦略誤りが、非常に複雑な疑似乱数の生成アルゴリズムが、
アルゴリズムの理論や分析なしに、強い乱数を作り出すであろうと想定する
ことです。[KNUTH]の3章の初めの近くに、著者が複雑なアルゴリズムを記
述する、この誤りの優秀な例があります。アルゴリズムに対応しているマシ
ン語プログラムがコメント無しでコードを読もうとしている人がプログラム
が何をしていたかわからないであろうほど複雑なことが意図されています。
不幸にも、このアルゴリズムを実際に使うとある場合は1つの値が繰り返さ
れて、他の場合は少ない種類の値の繰り返しを示しました。
Not only does complex manipulation not help you if you have a limited
range of seeds but blindly chosen complex manipulation can destroy
the randomness in a good seed!
単なる複雑な扱いが、もし種の範囲が限定されてる場合に役立たないだけで
なく、やみくもに選ばれた複雑な扱いが良い種の乱雑さを破壊することがで
きます!
4.4 The Fallacy of Selection from a Large Database
4.4 大きいデータベースからの選択の誤り
Another strategy that can give a misleading appearance of
unpredictability is selection of a quantity randomly from a database
and assume that its strength is related to the total number of bits
in the database. For example, typical USENET servers as of this date
process over 35 megabytes of information per day. Assume a random
quantity was selected by fetching 32 bytes of data from a random
starting point in this data. This does not yield 32*8 = 256 bits
worth of unguessability. Even after allowing that much of the data
is human language and probably has more like 2 or 3 bits of
information per byte, it doesn't yield 32*2.5 = 80 bits of
unguessability. For an adversary with access to the same 35
megabytes the unguessability rests only on the starting point of the
selection. That is, at best, about 25 bits of unguessability in this
case.
予知不可能さの紛らわしい出演を与えることができるもう1つの戦略がラン
ダムなデータベースからの数の選択で、その強度がデータベースのビットの
合計数と関係があると想定してください。例えば、典型的なUSENETサーバー
がこの日付の時点で1日に35メガバイトの情報を処理します。乱数がこの
データのランダムな出発点からの32バイトのデータを取り出すことで選ば
れたと想定してください。これは32*8 = 256ビットの予測不可能さを生じま
せん。データの多くが人間の言語であり、恐らく各バイト毎の情報量は2か
ら3ビット程度なので、これは32*2.5 = 80ビット程度の予測不能さしかもた
らしません。敵が同じ35メガバイトにアクセスできるなら、予測不能さは
選択の出発点だけになります。この場合、良くても、予測不能さはおよそ
25ビットです。
The same argument applies to selecting sequences from the data on a
CD ROM or Audio CD recording or any other large public database. If
the adversary has access to the same database, this "selection from a
large volume of data" step buys very little. However, if a selection
can be made from data to which the adversary has no access, such as
system buffers on an active multi-user system, it may be of some
help.
同じ議論はCD ROMや音声のCDレコードや他のいかなる大きい公共のデータ
ベースの上からデータ列を選ぶ場合にも当てはまります。もし敵が同じデー
タベースにアクセスできるなら、この「大量データからの選択」ステップは
極めて少ししか得られません。しかしながら、もし選択が、アクティブなマ
ルチユーザのシステムの上のシステムバッファのような、敵がアクセスでき
ないデータから作れるなら、いくらかの助けになるかもしれません。
5. Hardware for Randomness
5. ハードウェアの乱雑さ
Is there any hope for strong portable randomness in the future?
There might be. All that's needed is a physical source of
unpredictable numbers.
将来強力な携帯用の乱雑さの希望がありますか?あるかもしれません。必要
とされるすべては予想できない数の物理的なソースです。
A thermal noise or radioactive decay source and a fast, free-running
oscillator would do the trick directly [GIFFORD]. This is a trivial
amount of hardware, and could easily be included as a standard part
of a computer system's architecture. Furthermore, any system with a
spinning disk or the like has an adequate source of randomness
[DAVIS]. All that's needed is the common perception among computer
vendors that this small additional hardware and the software to
access it is necessary and useful.
熱雑音や放射性崩壊をソースにしたり、自由に発振する発信機が直接行う方
法でしょう[GIFFORD]。これはわずかな量のハードウェアで、容易にコンピュー
タシステムのアーキテクチャの標準的な部品として包含できます。さらに、
回転ディスクは同種の物を持つシステムが乱雑さの適切なソースです[DAVIS]。
必要なのは、この小さい追加のハードウェアとそれにアクセスするソフト
ウェアが必要で有用だというコンピュータのベンダー間の共通の理解です。
5.1 Volume Required
5.1 必要な量
How much unpredictability is needed? Is it possible to quantify the
requirement in, say, number of random bits per second?
どれぐらいの予測不能さが必要とされますか?必要条件を数量化して、ラン
ダム数ビット/秒と、言うことが可能ですか?
The answer is not very much is needed. For DES, the key is 56 bits
and, as we show in an example in Section 8, even the highest security
system is unlikely to require a keying material of over 200 bits. If
a series of keys are needed, it can be generated from a strong random
seed using a cryptographically strong sequence as explained in
Section 6.3. A few hundred random bits generated once a day would be
enough using such techniques. Even if the random bits are generated
as slowly as one per second and it is not possible to overlap the
generation process, it should be tolerable in high security
applications to wait 200 seconds occasionally.
答えはたくさんは必要ないです。DESの鍵は56ビットで、8章で見せる
ように、最も高いセキュリティシステムでさえ200ビット以上の鍵材料を
必要としなさそうです。もし一連の鍵が必要なら、6.3章で説明したよう
に、暗号的に強い数列を使って強いランダムな種から生成できます。1日1
度生成された数百のランダムビットが十分にこのようなテクニックに使える
でしょう。たとえランダムビットが1/秒とよりゆっくりと生成され、生成
プロセスと一致可能でないとしても、時々200秒待つことは高いセキュリ
ティアプリケーションで我慢できるべきです(SHOULD)。
These numbers are trivial to achieve. It could be done by a person
repeatedly tossing a coin. Almost any hardware process is likely to
be much faster.
これらの数は目的を達するために取るに足りません。これは繰り返しコイン
を投げ上げる人によってできます。ほとんどのハードウェアプロセスはもっ
と速い可能性が高いです。
5.2 Sensitivity to Skew
5.2 ゆがみに対する敏感さ
Is there any specific requirement on the shape of the distribution of
the random numbers? The good news is the distribution need not be
uniform. All that is needed is a conservative estimate of how non-
uniform it is to bound performance. Two simple techniques to de-skew
the bit stream are given below and stronger techniques are mentioned
in Section 6.1.2 below.
乱数の分散の形に特定の必要条件がありますか?良いニュースは分散が一様
である必要がないということです。必要なのは、非一様分布が性能と関係す
るかの、保守的な見積もりです。ビットストリームを真直ぐにする2つの単
純なテクニックが下で与えられます、もっと強いテクニックが下の6.1.2
章で言及されます。
5.2.1 Using Stream Parity to De-Skew
5.2.1 ゆがみを直すために流れのパリティを使う
Consider taking a sufficiently long string of bits and map the string
to "zero" or "one". The mapping will not yield a perfectly uniform
distribution, but it can be as close as desired. One mapping that
serves the purpose is to take the parity of the string. This has the
advantages that it is robust across all degrees of skew up to the
estimated maximum skew and is absolutely trivial to implement in
hardware.
十分に長いビット列を考えて、これを「0」か「1」に対応させます。対応
関係は完全に一様な分布をもたらさないでしょがう、望むのと近くなり得ま
す。目的を満たす1つの対応関係は列のパリティをとる事です。これは最大
限推定できるすべてのゆがみの程度に対して強靭で、ハードウェア実装が簡
単だという利点があります。
The following analysis gives the number of bits that must be sampled:
次の分析は試さなくてはならないビットの数を与えます:
Suppose the ratio of ones to zeros is 0.5 + e : 0.5 - e, where e is
between 0 and 0.5 and is a measure of the "eccentricity" of the
distribution. Consider the distribution of the parity function of N
bit samples. The probabilities that the parity will be one or zero
will be the sum of the odd or even terms in the binomial expansion of
(p + q)^N, where p = 0.5 + e, the probability of a one, and q = 0.5 -
e, the probability of a zero.
eを0から0.5の間の値で分散の「変」さの尺度とし、1と0の比率が
0.5 + e 対 0.5 - e とします。Nビットサンプルのパリティ関数の分布を考
えてください。パリティが1か0かは、 p を1の確率 p = 0.5 + e で q を
0の確率 q = 0.5 - e としたときに、2項展開式 (p + q)^N の偶数か奇数
の項の和によります。
These sums can be computed easily as
和が以下の様に簡単に計算できます
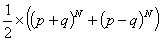
and
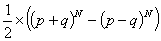
(Which one corresponds to the probability the parity will be 1
depends on whether N is odd or even.)
(Nが偶数か奇数かによりどちらかがパリティが1の確率です)
Since p + q = 1 and p - q = 2e, these expressions reduce to
p + q = 1 で p - q = 2e なので式が以下の様に短くできます。
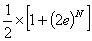
and
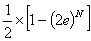
Neither of these will ever be exactly 0.5 unless e is zero, but we
can bring them arbitrarily close to 0.5. If we want the
probabilities to be within some delta d of 0.5, i.e. then
e がセロでなければこれらのいずれも正確に0.5ではありませんが、好き
なだけ0.5に近い数にできます。もし確率を0.5からデルタ d 以内にし
たければ以下の様にします。
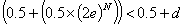
Solving for N yields N > log(2d)/log(2e). (Note that 2e is less than
1, so its log is negative. Division by a negative number reverses
the sense of an inequality.)
N について解くと N > log(2d)/log(2e) になります。(2eが1以下なので、
そのlogが負の値であることに注意してください。負数の割り算が不等式の意
味を逆にします。)。
The following table gives the length of the string which must be
sampled for various degrees of skew in order to come within 0.001 of
a 50/50 distribution.
以下の表はゆがみの度合いに対して、1対1の分散と0.001以内のゆがみに
するために必要なサンプルの長さを示します。
| Prob(1) |
e |
N |
0.5
0.6
0.7
0.8
0.9
0.95
0.99 |
0.00
0.10
0.20
0.30
0.40
0.45
0.49 |
1
4
7
13
28
59
308 |
The last entry shows that even if the distribution is skewed 99% in
favor of ones, the parity of a string of 308 samples will be within
0.001 of a 50/50 distribution.
最後の項目はたとえ分散の歪みが99%で1あるとしても、308のサンプ
ルビット列のパリティを取ると、1対1の分散と0.001以内の差であろうこ
とを示します。
5.2.2 Using Transition Mappings to De-Skew
5.2.2 歪みを直す翻訳マッピングの使用
Another technique, originally due to von Neumann [VON NEUMANN], is to
examine a bit stream as a sequence of non-overlapping pairs. You
could then discard any 00 or 11 pairs found, interpret 01 as a 0 and
10 as a 1. Assume the probability of a 1 is 0.5+e and the
probability of a 0 is 0.5-e where e is the eccentricity of the source
and described in the previous section. Then the probability of each
pair is as follows:
もう1つのテクニックが、フォン・ノイマン[VON NEUMANN]が作ったもので、
重複しない対のビット列を調べる方法です。出てきた00や11の対は捨て
て、01を0と考え10を1と考えます。e を前の章で記述したものとし、
1の可能性が 0.5+e で、0の可能性が 0.5-e あると想定してください。各
対の発生率は次の通りです:
pair
ペア |
probability
確率 |
00
01
10
11 |
(0.5 - e)^2 = 0.25 - e + e^2
(0.5 - e)*(0.5 + e) = 0.25 - e^2
(0.5 + e)*(0.5 - e) = 0.25 - e^2
(0.5 + e)^2 = 0.25 + e + e^2
|
This technique will completely eliminate any bias but at the expense
of taking an indeterminate number of input bits for any particular
desired number of output bits. The probability of any particular
pair being discarded is 0.5 + 2e^2 so the expected number of input
bits to produce X output bits is X/(0.25 - e^2).
このテクニックは完全にどんな歪みを排除しますが、望ましい出力に対して
必要な入力は不確定です。捨てられる対の可能性は 0.5 + 2e^2 で、Xビット
の出力を得るのに期待される入力のビット数はX/(0.25 - e^2)です。
This technique assumes that the bits are from a stream where each bit
has the same probability of being a 0 or 1 as any other bit in the
stream and that bits are not correlated, i.e., that the bits are
identical independent distributions. If alternate bits were from two
correlated sources, for example, the above analysis breaks down.
このテクニックは各ビットが0か1かである確率が他のビットに関係なく同
じで、ビットが関係していない、すなわちビットが独立分布であるビット列
を想定します。例えばもし2つの関連したソースから交互に出たビットであ
るなら、上記の分析は破綻します。
The above technique also provides another illustration of how a
simple statistical analysis can mislead if one is not always on the
lookout for patterns that could be exploited by an adversary. If the
algorithm were mis-read slightly so that overlapping successive bits
pairs were used instead of non-overlapping pairs, the statistical
analysis given is the same; however, instead of provided an unbiased
uncorrelated series of random 1's and 0's, it instead produces a
totally predictable sequence of exactly alternating 1's and 0's.
上記のテクニックは、敵が利用できるパターンを常に見張っていないと、ど
のように簡単な統計分析が誤りを導くかの、他の例を提供します。もしアル
ゴリズムがわずかに読み間違えをして、重複しない対ではなく、重複する連
続ビット対を使うなら、与えられた統計上の分析は同じです;しかし、ラン
ダムな0と1のそれの公平で相関のない列ではなく、0と1が交互に現れる
予測可能な列を発生させます。
5.2.3 Using FFT to De-Skew
5.2.3 歪みを直すFFTの使用
When real world data consists of strongly biased or correlated bits,
it may still contain useful amounts of randomness. This randomness
can be extracted through use of the discrete Fourier transform or its
optimized variant, the FFT.
真の世界データが強く偏っているか相関したビットから成り立っていても、
まだランダムさの有用な部分を含んでいるかもしれません。このランダムさ
は離散フーリエ変換かその最適化した変形FFTによって抜きだす事ができ
るかもしれません。
Using the Fourier transform of the data, strong correlations can be
discarded. If adequate data is processed and remaining correlations
decay, spectral lines approaching statistical independence and
normally distributed randomness can be produced [BRILLINGER].
データのフーリエ変換を使うと、強い相関を捨ることができます。もし適切
なデータが処理され、残っている相関を捨てれば、統計的に独立に近いスペ
クトルラインと通常の分散乱雑さを作り出す事ができます[BRILLINGER]。
5.2.4 Using Compression to De-Skew
5.2.4 歪みを直す圧縮の使用
Reversible compression techniques also provide a crude method of de-
skewing a skewed bit stream. This follows directly from the
definition of reversible compression and the formula in Section 2
above for the amount of information in a sequence. Since the
compression is reversible, the same amount of information must be
present in the shorter output than was present in the longer input.
By the Shannon information equation, this is only possible if, on
average, the probabilities of the different shorter sequences are
more uniformly distributed than were the probabilities of the longer
sequences. Thus the shorter sequences are de-skewed relative to the
input.
元に戻せる圧縮テクニックが同じくそのままで歪んだビット列を直す方法を
供給します。これは元に戻せる圧縮の定義と上記2章の列の情報量の公式か
ら当然生じます。圧縮が元に戻せるので、長い入力と短い出力は同じ情報量
に違いありません。シャノン情報式によって、これはもし平均して異なる短
い列の確率がより長い列の確率より一様分布である場合にだけ可能です。そ
れで短い連列は入力と比較して歪みがないです。
However, many compression techniques add a somewhat predicatable
preface to their output stream and may insert such a sequence again
periodically in their output or otherwise introduce subtle patterns
of their own. They should be considered only a rough technique
compared with those described above or in Section 6.1.2. At a
minimum, the beginning of the compressed sequence should be skipped
and only later bits used for applications requiring random bits.
しかしながら、多くの圧縮テクニックが出力列に幾分予測可能な前書きを加
えて、周期的に出力にこのような列を挿入するか、それら自身の敏感なパター
ンを導入します。これらは上記や6.1.2章と比較して雑なテクニックだけ
であると思われるべきです。最小限、圧縮列の初めは飛ばして、ランダムビッ
トを必要としているアプリケーションが使うのは後ビットだけにするべきで
す。
5.3 Existing Hardware Can Be Used For Randomness
5.3 の既存ハードウェアが乱雑さに使えます
As described below, many computers come with hardware that can, with
care, be used to generate truly random quantities.
下記述のように、多くのコンピュータが、注意して使えば、本当の乱数を生
成するのに使えるハードウェアを持っています。
5.3.1 Using Existing Sound/Video Input
5.3.1 既存の音声/ビデオ入力の使用
Increasingly computers are being built with inputs that digitize some
real world analog source, such as sound from a microphone or video
input from a camera. Under appropriate circumstances, such input can
provide reasonably high quality random bits. The "input" from a
sound digitizer with no source plugged in or a camera with the lens
cap on, if the system has enough gain to detect anything, is
essentially thermal noise.
コンピュータに、マイクからの音やカメラからの映像のような、実世界アナ
ログソースをデジタル化する入力が組み込まれるようになってきています。
適切な状況下で、このような入力は相応に高品質のランダムビットを供給し
ます。何もつながっていないデジタル化音入力や、レンズキャップがされた
ままのカメラからの入力が、システムが十分な利得を持っていれば、これは
本質的に熱雑音です。
For example, on a SPARCstation, one can read from the /dev/audio
device with nothing plugged into the microphone jack. Such data is
essentially random noise although it should not be trusted without
some checking in case of hardware failure. It will, in any case,
need to be de-skewed as described elsewhere.
例えば、 SPARCstation上で、マイクロホンジャックに何も差し込まずに
/dev/audioデバイスから読み込むことができます。このようなデータは、ハー
ドウェア故障のいくつかの検査無しで信頼するべきではないが、本質的にラ
ンダムな雑音です。これは、どんな場合でも、他で記述されるように、歪み
を直す必要があるでしょう。
Combining this with compression to de-skew one can, in UNIXese,
generate a huge amount of medium quality random data by doing
歪みを直すため圧縮を使うと、UNIXで、以下によって巨大な量の中間の
品質のランダムデータを生成できます。
cat /dev/audio | compress - >random-bits-file
5.3.2 Using Existing Disk Drives
5.3.2 既存ディスク・ドライブを使う
Disk drives have small random fluctuations in their rotational speed
due to chaotic air turbulence [DAVIS]. By adding low level disk seek
time instrumentation to a system, a series of measurements can be
obtained that include this randomness. Such data is usually highly
correlated so that significant processing is needed, including FFT
(see section 5.2.3). Nevertheless experimentation has shown that,
with such processing, disk drives easily produce 100 bits a minute or
more of excellent random data.
ディスク・ドライブが無秩序な空気の乱流のために回転速度に小さいランダ
ム変動を持ちます[DAVIS]。システムに低レベルディスクシーク時間測定を
加えることで、この乱雑さを含む一連の測定が得られます。このようなデー
タは通常相関があり、FFT含む有意義な処理が必要です(5.2.3章参照)。
にもかかわらず、実験によって、このような処理で、ディスクドライブが容
易に1分間に100ビット以上の優秀なランダムなデータを作り出せる事が
示されました。
Partly offsetting this need for processing is the fact that disk
drive failure will normally be rapidly noticed. Thus, problems with
this method of random number generation due to hardware failure are
very unlikely.
この処理の必要性に対する利点は、ディスク・ドライブ故障が通常直ぐに気
付かれるであろうという事実です。それで、ハードウェア故障のための乱数
生成の問題はほとんどなさそうです。
6. Recommended Non-Hardware Strategy
6. 推薦された非ハードウェアの戦略
What is the best overall strategy for meeting the requirement for
unguessable random numbers in the absence of a reliable hardware
source? It is to obtain random input from a large number of
uncorrelated sources and to mix them with a strong mixing function.
信頼性が高いハードウェアソースがない場合、予測不可能な乱数の必要条件
を満たすことに対する最も良い全体的な戦略は何ですか?それは多数の相関
のないソースからランダム入力を得て、それらを強力な混合関数で混ぜる事
です。
Such a function will preserve the randomness present in any of the
sources even if other quantities being combined are fixed or easily
guessable. This may be advisable even with a good hardware source as
hardware can also fail, though this should be weighed against any
increase in the chance of overall failure due to added software
complexity.
このような関数は、たとえ結合されている他の量が固定しているか、あるい
は容易に予測できても、ソースのそれぞれに存在している乱雑さを維持する
でしょう。これは、付加的なソフトウェアの複雑さのために全体的な失敗の
可能性の増加が熟考されるべきであるが、ハードウェアが故障することがあ
るので、良いハードウェアソースを使う場合でも賢明かもしれません。
6.1 Mixing Functions
6.1 混合関数
A strong mixing function is one which combines two or more inputs and
produces an output where each output bit is a different complex non-
linear function of all the input bits. On average, changing any
input bit will change about half the output bits. But because the
relationship is complex and non-linear, no particular output bit is
guaranteed to change when any particular input bit is changed.
混合関数は2つ以上の入力を結合し、その出力ビットがそれぞれ異なった全
ての入力の複雑で線形でない関数であるものです。平均して、入力ビットの
任意のビットの変化が、出力の半分のビットを変化させるでしょう。けれど
も関連が複雑で非線形であるから、入力の特定のビットが変化したときに、
出力のどのビットが変化するか予測できません。
Consider the problem of converting a stream of bits that is skewed
towards 0 or 1 to a shorter stream which is more random, as discussed
in Section 5.2 above. This is simply another case where a strong
mixing function is desired, mixing the input bits to produce a
smaller number of output bits. The technique given in Section 5.2.1
of using the parity of a number of bits is simply the result of
successively Exclusive Or'ing them which is examined as a trivial
mixing function immediately below. Use of stronger mixing functions
to extract more of the randomness in a stream of skewed bits is
examined in Section 6.1.2.
上記5.2章で論じられるように、0か1の方向に傾いてるビット列をより短
いランダム列に変換する問題を考えてください。これは、入力ビットを混ぜ
て短い出力ビットを生成する、強力な混合機能の要望される他の例です。セ
クション5.2.1章で与えられた多数のビットのパリティのテクニックは、
連続した排他的論理和の結果で、以下のつまらない混合関数です。歪んだビッ
ト列の中からより多くの乱雑さを引き出すより強力な混合関数の使用が
6.1.2章で調べられます。
6.1.1 A Trivial Mixing Function
6.1.1 つまらない混合関数
A trivial example for single bit inputs is the Exclusive Or function,
which is equivalent to addition without carry, as show in the table
below. This is a degenerate case in which the one output bit always
changes for a change in either input bit. But, despite its
simplicity, it will still provide a useful illustration.
1ビット入力ののためのつまらない例は、排他的論理和関数で、これはパリ
ティなしの加算と等しく、以下の表の通りです。これはどの入力の変化に対
しても出力ビットが変化するよくない場合です。けれども、その単純にもか
かわらず、これは有用な例を供給するでしょう。
input1
入力1 |
input2
入力2 |
output
出力 |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
If inputs 1 and 2 are uncorrelated and combined in this fashion then
the output will be an even better (less skewed) random bit than the
inputs. If we assume an "eccentricity" e as defined in Section 5.2
above, then the output eccentricity relates to the input eccentricity
as follows:
もし入力1と2に相関がなくて、この機能で結合されるなら、出力はもっと
入力より良い(より歪みの少ない)ランダムビットでしょう。もし、上記に
5.2章で定義されるように、「歪み」eを仮定するなら、出力の歪みは次の
ように入力の歪みと関連しています:
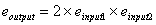
Since e is never greater than 1/2, the eccentricity is always
improved except in the case where at least one input is a totally
skewed constant. This is illustrated in the following table where
the top and left side values are the two input eccentricities and the
entries are the output eccentricity:
eが決して1/2よりおおきくないので、少なくとも1つの入力が完全に歪
んだ定数である場合を除いて、歪みが常に改善されます。これは以下の表で
示せます、表の上と左が2つの入力のゆがみで、項目が出力の歪みです:
| e |
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
0.50 |
| 0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
| 0.10 |
0.00 |
0.02 |
0.04 |
0.06 |
0.08 |
0.10 |
| 0.20 |
0.00 |
0.04 |
0.08 |
0.12 |
0.16 |
0.20 |
| 0.30 |
0.00 |
0.06 |
0.12 |
0.18 |
0.24 |
0.30 |
| 0.40 |
0.00 |
0.08 |
0.16 |
0.24 |
0.32 |
0.40 |
| 0.50 |
0.00 |
0.10 |
0.20 |
0.30 |
0.40 |
0.50 |
However, keep in mind that the above calculations assume that the
inputs are not correlated. If the inputs were, say, the parity of
the number of minutes from midnight on two clocks accurate to a few
seconds, then each might appear random if sampled at random intervals
much longer than a minute. Yet if they were both sampled and
combined with xor, the result would be zero most of the time.
しかしながら、上記の計算が入力に相関がないと想定してることを念頭にお
いてください。もし入力が秒単位で正確な2つの時計での真夜中からの分数
のパリティであり、それぞれが1分より長いランダムな間隔でサンプルされ
るなら、ランダムに見えるかもしれません。もしそれらが共にサンプルされ
て、XORされたら、結果はほとんどいつもゼロでしょう。
6.1.2 Stronger Mixing Functions
6.1.2 強力な混合関数
The US Government Data Encryption Standard [DES] is an example of a
strong mixing function for multiple bit quantities. It takes up to
120 bits of input (64 bits of "data" and 56 bits of "key") and
produces 64 bits of output each of which is dependent on a complex
non-linear function of all input bits. Other strong encryption
functions with this characteristic can also be used by considering
them to mix all of their key and data input bits.
合衆国政府データ暗号化規格[DES]は多数のビットの強力な混合関数の例です。
これは120ビット以上の入力(64ビットの「データ」と56ビットの
「キー」)をとり、64ビットの出力を生成し、各出力ビットは独立で全て
の入力ビットに対する非線形の複雑な出力になります。他の強力な暗号関数
が、その特徴から、同じくすべての鍵ととデータ入力ビットを混ぜると考え
ることで、混合関数に使えます。
Another good family of mixing functions are the "message digest" or
hashing functions such as The US Government Secure Hash Standard
[SHS] and the MD2, MD4, MD5 [MD2, MD4, MD5] series. These functions
all take an arbitrary amount of input and produce an output mixing
all the input bits. The MD* series produce 128 bits of output and SHS
produces 160 bits.
他の良い混合関数が、合衆国政府セキュアハッシュ標準[SHS]やMD2、MD
3、MD5シリーズのような、「メッセージダイジェスト」あるいはハッ
シュ関数です。これらの関数はすべて任意の量の入力をとり、すべての入力
ビットを混ぜた出力を引き起こします。MD*シリーズが128ビットの出
力を起こし、SHSは160ビットを作り出します。
Although the message digest functions are designed for variable
amounts of input, DES and other encryption functions can also be used
to combine any number of inputs. If 64 bits of output is adequate,
the inputs can be packed into a 64 bit data quantity and successive
56 bit keys, padding with zeros if needed, which are then used to
successively encrypt using DES in Electronic Codebook Mode [DES
MODES]. If more than 64 bits of output are needed, use more complex
mixing. For example, if inputs are packed into three quantities, A,
B, and C, use DES to encrypt A with B as a key and then with C as a
key to produce the 1st part of the output, then encrypt B with C and
then A for more output and, if necessary, encrypt C with A and then B
for yet more output. Still more output can be produced by reversing
the order of the keys given above to stretch things. The same can be
done with the hash functions by hashing various subsets of the input
data to produce multiple outputs. But keep in mind that it is
impossible to get more bits of "randomness" out than are put in.
メッセージダイジェスト関数が可変長の入力のために設計されるが、DES
と他の暗号化機能が任意の入力数を混ぜるために同じく使うことができます。
もし64ビット出力が必要なら、もし必要なら0のパディングをして、入力
は64ビットデータと56ビット鍵にして、これを電子コードブックモード
のDESを使って連続的に暗号化できます[DES MODES]。もし64ビット以上
の出力が必要なら、より複雑な混合を使います。例えば、もし入力をAとB
とCの3つに分けるなら、DES暗号を使ってAと鍵Bで暗号化したものを
さらに鍵Cで暗号化し最初の出力とし、Bを鍵Cと鍵Aで暗号化したものを
2番目の出力とし、必要ならCを鍵Aと鍵Bで暗号化したものを追加の出力
とします。さらの多くの出力、がかぎの順序を入れ替えて引き伸ばすことで、
生成できます。入力の様々な部分をハッシュ関数に通すことで、同じ用に多
数の出力を得られます。しかし、入力より多くの乱雑さの出力を得ることが
不可能である事を念頭においてください。
An example of using a strong mixing function would be to reconsider
the case of a string of 308 bits each of which is biased 99% towards
zero. The parity technique given in Section 5.2.1 above reduced this
to one bit with only a 1/1000 deviance from being equally likely a
zero or one. But, applying the equation for information given in
Section 2, this 308 bit sequence has 5 bits of information in it.
Thus hashing it with SHS or MD5 and taking the bottom 5 bits of the
result would yield 5 unbiased random bits as opposed to the single
bit given by calculating the parity of the string.
強力な混合関数を使う例は、各ビットが99%ゼロに偏っている308ビッ
トの文字列の場合を再考するでしょう。上記5.2.1章で与えたテクニック
は、0と1の確率が等しいのから1/1000だけずれた1ビットを生成し
ました。しかし、2章で与えた情報式を適用すると、この308のビット列
はその中に5ビットの情報を持っています。したがって、SHSやMD5ハッ
シュを行って、下位5ビットを取ると、同じ文字列から1ビットを計算と比
べて、5つの公平なランダムなビットをもたらすでしょう。
6.1.3 Diffie-Hellman as a Mixing Function
6.1.3 混合関数としてのDiffie-Hellman
Diffie-Hellman exponential key exchange is a technique that yields a
shared secret between two parties that can be made computationally
infeasible for a third party to determine even if they can observe
all the messages between the two communicating parties. This shared
secret is a mixture of initial quantities generated by each of them
[D-H]. If these initial quantities are random, then the shared
secret contains the combined randomness of them both, assuming they
are uncorrelated.
Diffie-Hellmanの指数関数的な鍵交換は、第三者がたとえ2者間のすべての
通信メッセージを観察できても計算量的に鍵がばれない様に、2者間に共有
秘密鍵をもたらすテクニックです。この共有秘密鍵は彼らのそれぞれから生
成される初期値の混合です[D-H]。もしこれらの初期値がランダムなら、共
有秘密鍵は、それらが相関がないと想定すると、それら両方を結合した乱雑
さを含んでいます。
6.1.4 Using a Mixing Function to Stretch Random Bits
6.1.4 ランダムビットを拡張するための混合関数の使用
While it is not necessary for a mixing function to produce the same
or fewer bits than its inputs, mixing bits cannot "stretch" the
amount of random unpredictability present in the inputs. Thus four
inputs of 32 bits each where there is 12 bits worth of
unpredicatability (such as 4,096 equally probable values) in each
input cannot produce more than 48 bits worth of unpredictable output.
The output can be expanded to hundreds or thousands of bits by, for
example, mixing with successive integers, but the clever adversary's
search space is still 2^48 possibilities. Furthermore, mixing to
fewer bits than are input will tend to strengthen the randomness of
the output the way using Exclusive Or to produce one bit from two did
above.
入力と同じか短いビットを生成する事は混合関数に必要ありませんが、ビッ
トを混ぜて入力ランダムの予測不能さの量を存在している以上に「増やす」
ことはできません。それぞれ12ビットの予測不能さをもつ4つの32ビッ
ト入力から(4,096の等しくありそうな値と同様)から、48ビット以
上の予測不能さをもった出力を生成できません。連続した数と混ぜ合わせる
ことで出力は数百ビットでも数千ビットにでも拡張できますが、利口な敵が
捜索する空間は2^48のままです。さらに、入力より少ないビットに混ぜ
ることは、前の2ビットから排他的論理和で1ビットを生成する方法を使っ
て、出力の乱雑さを強固にする傾向があるでしょう。
The last table in Section 6.1.1 shows that mixing a random bit with a
constant bit with Exclusive Or will produce a random bit. While this
is true, it does not provide a way to "stretch" one random bit into
more than one. If, for example, a random bit is mixed with a 0 and
then with a 1, this produces a two bit sequence but it will always be
either 01 or 10. Since there are only two possible values, there is
still only the one bit of original randomness.
6.1.1章の最後の表じゃランダムビットと定数の排他的論理和がランダム
ビットを生成することを示します。これが真実ではあっても、1ビットを2
ビット以上のランダムに「拡張する」方法を供給しません。もし、例えば、
ランダムビットを0と1で混ぜたら2ビット列を作り出しますが、これは常
に01か10でしょう。可能な値は2つだけなので、元々の乱雑さの1ビッ
トのままです。
6.1.5 Other Factors in Choosing a Mixing Function
6.1.5 混合関数を選択する他の要因
For local use, DES has the advantages that it has been widely tested
for flaws, is widely documented, and is widely implemented with
hardware and software implementations available all over the world
including source code available by anonymous FTP. The SHS and MD*
family are younger algorithms which have been less tested but there
is no particular reason to believe they are flawed. Both MD5 and SHS
were derived from the earlier MD4 algorithm. They all have source
code available by anonymous FTP [SHS, MD2, MD4, MD5].
ローカルな使用では、DESが広く欠陥についてテストされ、広く文書化さ
れ、匿名FTPによって利用可能なソースコードを含めて全世界に利用可能
なハードウェアとソフトウェア実装が広くあるという利点を持ちます。SH
SとMD*ファミリ−はテストが少ないより若いアルゴリズムですが、それ
らに問題がある信じる特定の理由がありません。MD5とSHSの両方がよ
り初期のMD4アルゴリズムから得られました。これらはすべて匿名FTP
によって利用可能なソースコードを持ちます[SHS, MD2, MD4, MD5]。
DES and SHS have been vouched for the the US National Security Agency
(NSA) on the basis of criteria that primarily remain secret. While
this is the cause of much speculation and doubt, investigation of DES
over the years has indicated that NSA involvement in modifications to
its design, which originated with IBM, was primarily to strengthen
it. No concealed or special weakness has been found in DES. It is
almost certain that the NSA modification to MD4 to produce the SHS
similarly strengthened the algorithm, possibly against threats not
yet known in the public cryptographic community.
DESとSHSが、秘密の基準によって合衆国国家安全保障局(NSA)に
保証されています。これがたくさんの推測と疑いの原因になっていたが、数
年間かけてのDESの調査が、IBMが元々作ったデザインに対する修正の
NSAのかかわり合いが、主に強化であったことをを示しました。秘密や特
別な欠点がDESに見いだされませんでした。同様にSHSを作り出すため
のMD4へのNSAの修正が、多分公開暗号社会でまだ周知でない脅しに対
しての、アルゴリズムの強固である事はほとんど確かです。
DES, SHS, MD4, and MD5 are royalty free for all purposes. MD2 has
been freely licensed only for non-profit use in connection with
Privacy Enhanced Mail [PEM]. Between the MD* algorithms, some people
believe that, as with "Goldilocks and the Three Bears", MD2 is strong
but too slow, MD4 is fast but too weak, and MD5 is just right.
DESとSHSとMD4とMD5はすべての目的の使用でロイヤリティフリー
です。MD2がプライバシ拡張メール[PEM]に関連した非営利の使用にだけ自
由な利用が許可されました。MD*アルゴリズム間で、ある人々は信じてい
ます、「ゴールディロックスちゃんと3匹の熊」で、MD2が強いが遅く、
MD4が早いが弱く、MD5がちょうどよいと信じます。
訳注:「The goldilocks and the three bears」はイギリスの民話かな
にかで、ほどほどがよいという意味で使われるようです。
日本では「3びきのくま」といったタイトルで絵本になっています。
Another advantage of the MD* or similar hashing algorithms over
encryption algorithms is that they are not subject to the same
regulations imposed by the US Government prohibiting the unlicensed
export or import of encryption/decryption software and hardware. The
same should be true of DES rigged to produce an irreversible hash
code but most DES packages are oriented to reversible encryption.
もう1つのMD*や類似のハッシュアルゴリズムの暗号化アルゴリズムに対
する利点は、合衆国政府による無許可の暗号化/解読ソフトウェアとハード
ウェアの輸出と輸入の規制を受けないということです。同じ事が非可逆的ハッ
シュコードのためのDESにいえるべきですが、たいていのDESパッケー
ジが可逆的暗号化向きです。
6.2 Non-Hardware Sources of Randomness
6.2 乱雑の非ハードウェアソース
The best source of input for mixing would be a hardware randomness
such as disk drive timing affected by air turbulence, audio input
with thermal noise, or radioactive decay. However, if that is not
available there are other possibilities. These include system
clocks, system or input/output buffers, user/system/hardware/network
serial numbers and/or addresses and timing, and user input.
Unfortunately, any of these sources can produce limited or
predicatable values under some circumstances.
混合の入力の最も良いソースは、空気乱流の影響を受けるディスク・ドライ
ブタイミングや、熱雑音の音声入力や、放射性崩壊のようなハードウェア乱
雑です。しかしながら、もしそれが利用可能ではないなら、他の可能性があ
ります。これらはシステム時計、システムや入出力バッファ、ユーザー/シ
ステム/ハードウェア/ネットワークシリアル番号かアドレス、タイミング
とユーザー入力を含みます。不幸にも、これらのソースのどれもある状況下
で限定されているか決定できる値を作り出します。
Some of the sources listed above would be quite strong on multi-user
systems where, in essence, each user of the system is a source of
randomness. However, on a small single user system, such as a
typical IBM PC or Apple Macintosh, it might be possible for an
adversary to assemble a similar configuration. This could give the
adversary inputs to the mixing process that were sufficiently
correlated to those used originally as to make exhaustive search
practical.
上にリストアップされたソースのいくつかか、本質的に、各システムユーザー
が乱雑さの源であるマルチユーザシステムに非常に強いでしょう。しかしな
がら、典型的なIBM PCやアップル・マッキントッシュのような、小さい一人
のユーザーシステム上で敵が類似の設定の組み立てが可能かもしれません。
これはしらみつぶしの捜索を実用的にするのに十分なぐらい、混合入力プロ
セスの入力を敵に与えることができます。
The use of multiple random inputs with a strong mixing function is
recommended and can overcome weakness in any particular input. For
example, the timing and content of requested "random" user keystrokes
can yield hundreds of random bits but conservative assumptions need
to be made. For example, assuming a few bits of randomness if the
inter-keystroke interval is unique in the sequence up to that point
and a similar assumption if the key hit is unique but assuming that
no bits of randomness are present in the initial key value or if the
timing or key value duplicate previous values. The results of mixing
these timings and characters typed could be further combined with
clock values and other inputs.
多数のランダム入力を伴う強い混合関数の使用が勧められて、多数の入力が
特定の入力の弱さを克服できます。例えば、「ランダム」ユーザーキースト
ロークのタイミングと内容は何百ビットものランダムなビットもをもたらし
ますが、しかし保守的な仮定を作る必要があります。例えば、もしキースト
ローク間の間隔がユニークなら数ビットの数ビットの乱雑さを仮定でき、も
し打たれたキーがユニークなら同様の仮定ができますが、最初のキー値や同
じ値の繰り返しの時の間隔やキー値に乱雑さがないと想定できます。これら
のタイミングとタイプされた文字の混合の結果はさらに時計値と他の入力と
一緒にできます。
This strategy may make practical portable code to produce good random
numbers for security even if some of the inputs are very weak on some
of the target systems. However, it may still fail against a high
grade attack on small single user systems, especially if the
adversary has ever been able to observe the generation process in the
past. A hardware based random source is still preferable.
この戦略は、たとえ入力のいくつかが目標システム上で非常に弱いとしても、
セキュリティのための良い乱数を作り出すための実際的移植可能コードにな
るかもしれません。しかしながら、それは、特にもし敵が過去に発生プロセ
スを観察することが可能であったなら、小さい一人のユーザーシステムに対
する高級な攻撃に対して失敗するかもしれません。ハードウェアに基づくラ
ンダムソースがまだ望ましいです。
6.3 Cryptographically Strong Sequences
6.3 暗号的に強い列
In cases where a series of random quantities must be generated, an
adversary may learn some values in the sequence. In general, they
should not be able to predict other values from the ones that they
know.
一連の乱数が生成された場合、敵が連続値のいくらかを学べるでしょう。一
般に、敵が知っている値から他の値を予測可能であるべきではありません。
The correct technique is to start with a strong random seed, take
cryptographically strong steps from that seed [CRYPTO2, CRYPTO3], and
do not reveal the complete state of the generator in the sequence
elements. If each value in the sequence can be calculated in a fixed
way from the previous value, then when any value is compromised, all
future values can be determined. This would be the case, for
example, if each value were a constant function of the previously
used values, even if the function were a very strong, non-invertible
message digest function.
正しいテクニックは初めは強いランダムな種で初めて、その種から暗号的に
強い手順を取り[CRYPTO2, CRYPTO3]、連続要素で生成機の完全な状態を明ら
かにしないことです。もし各連続値が前の値から固定した方法で計算され得
るなら、ある値が危険になると、すべての未来の値は決定されてしまいます。
これは、各値が、たとえ関数が非常に強力な非可逆メッセージダイジェスト
関数であったとしても、前の値からの定数関数であったら真実です。
It should be noted that if your technique for generating a sequence
of key values is fast enough, it can trivially be used as the basis
for a confidentiality system. If two parties use the same sequence
generating technique and start with the same seed material, they will
generate identical sequences. These could, for example, be xor'ed at
one end with data being send, encrypting it, and xor'ed with this
data as received, decrypting it due to the reversible properties of
the xor operation.
もし鍵値列を生成するテクニックが十分に速いなら、それが平凡に機密性シ
ステムの基盤として使うことができることを指摘します。もし2者が同じビッ
ト列生成テクニックを使い、同じ種から生成し始めるなら、それらは同一の
ビット列を生成するでしょう。これらはXORの可逆的な性質のため、例え
ば、片側でデータのXORを行い暗号化したデータを送信し、受信したデー
タとXORを取ってデータを復号化します。
6.3.1 Traditional Strong Sequences
6.3.1 伝統的な強い列
A traditional way to achieve a strong sequence has been to have the
values be produced by hashing the quantities produced by
concatenating the seed with successive integers or the like and then
mask the values obtained so as to limit the amount of generator state
available to the adversary.
強いビット列を生成する伝統的な方法は、連続した値の整数あるいは同種の
ものと種を結合してハッシュをし、次に敵が入手可能な生成状態の量を制限
するため得られた値をマスクすることでした。
It may also be possible to use an "encryption" algorithm with a
random key and seed value to encrypt and feedback some or all of the
output encrypted value into the value to be encrypted for the next
iteration. Appropriate feedback techniques will usually be
recommended with the encryption algorithm. An example is shown below
where shifting and masking are used to combine the cypher output
feedback. This type of feedback is recommended by the US Government
in connection with DES [DES MODES].
これはランダム鍵と種値と「暗号化」アルゴリズムを使用して、暗号化した
出力の一部か全部を次の繰り返し入力に戻す事でも可能かもしれません。適
切なフィードバックテクニックが通常暗号化アルゴリズムで推薦されるでしょ
う。以下の例では、シフトとマスクが暗号出力の結合に使われます。このタ
イプのフィードバックがDES[DES MODES]に関連して合衆国政府によって勧め
られます。
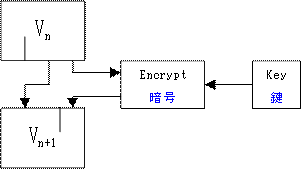
Note that if a shift of one is used, this is the same as the shift
register technique described in Section 3 above but with the all
important difference that the feedback is determined by a complex
non-linear function of all bits rather than a simple linear or
polynomial combination of output from a few bit position taps.
もし1ビットシフトが使われるなら、これは3章で記述されるシフトレジス
タテクニックと同じであるが、フィードバックが出力の数ビット位置の単純
な線形か多項式結合ではなく、すべてのビットの複雑な非線形関数で決定さ
れるという極めて重要な相違があることに注意してください。
It has been shown by Donald W. Davies that this sort of shifted
partial output feedback significantly weakens an algorithm compared
will feeding all of the output bits back as input. In particular,
for DES, repeated encrypting a full 64 bit quantity will give an
expected repeat in about 2^63 iterations. Feeding back anything less
than 64 (and more than 0) bits will give an expected repeat in
between 2**31 and 2**32 iterations!
この種の部分的出力のフィードバックとシフトが、全ての出力ビットを入力
に戻すのと比べて弱いアルゴリズムであることが、ドナルド・W・デイビー
ズによって明らかにされました。特にDESで、64ビットの全ての暗号化
の繰り返しが、2^63周期の繰り返しが期待されます。64ビット未満
(そして0より多い)のフィードバックは、2^31か2^32周期の繰り
返しを与えるでしょう!
To predict values of a sequence from others when the sequence was
generated by these techniques is equivalent to breaking the
cryptosystem or inverting the "non-invertible" hashing involved with
only partial information available. The less information revealed
each iteration, the harder it will be for an adversary to predict the
sequence. Thus it is best to use only one bit from each value. It
has been shown that in some cases this makes it impossible to break a
system even when the cryptographic system is invertible and can be
broken if all of each generated value was revealed.
ビット列がこれらのテクニックによって生み出された時、他のものから連続
の値を予言することは暗号システムを壊すか、部分的な情報が利用可能な状
態で、関係している「非可逆」ハッシュの逆計算をすることに等しいです。
各繰り返しで、より少しの情報だけが明らかにされたら、それだけ敵がビッ
ト列を予言するのが難しいでしょう。それで各値からただ1ビットだけを使
うことが最も良いです。これはある場合に、暗号システムが可逆的で、もし
生成された値の全てが明らかになると暗号システムが壊れる場合も、部分的
なビットではシステムを壊すことが不可能なことが明らかにされています。
6.3.2 The Blum Blum Shub Sequence Generator
6.3.2 Blum Blum Shub列生成機
Currently the generator which has the strongest public proof of
strength is called the Blum Blum Shub generator after its inventors
[BBS]. It is also very simple and is based on quadratic residues.
It's only disadvantage is that is is computationally intensive
compared with the traditional techniques give in 6.3.1 above. This
is not a serious draw back if it is used for moderately infrequent
purposes, such as generating session keys.
現在力の最も強い公共の証明を持つ生成機はその発明者[BBS]によっての
Blum Blum Shub生成機と呼ばれます。これは非常に単純で、二次の残余に基
づいています。この欠点はこれが上記6.3.1の伝統的な技術と比較して計
算量的に集約的な点です。これはもしそれがセッションキーを生成するよう
な適度にまれな目的のために使われるなら重大な欠点ではありません。
Simply choose two large prime numbers, say p and q, which both have
the property that you get a remainder of 3 if you divide them by 4.
Let n = p * q. Then you choose a random number x relatively prime to
n. The initial seed for the generator and the method for calculating
subsequent values are then
4で割ると余りが3である性質を持ってる2つの大きい素数pとqを選択して
ください。n = p * qとします。それからnと互いに素な乱数xを選択します。
生成機の最初の種値と次の値を計算する方法は以下です。
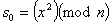
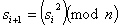
You must be careful to use only a few bits from the bottom of each s.
It is always safe to use only the lowest order bit. If you use no
more than the
各sの底から数ビットだけを使うように気を使わなくてはなりません。最下位
ビットだけを使うことが常に安全です。次を越える下位ビット使うなら、
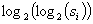
low order bits, then predicting any additional bits from a sequence
generated in this manner is provable as hard as factoring n. As long
as the initial x is secret, you can even make n public if you want.
この方法で生成されたビット列から追加ビットを予測することはnを因数分
解するのと比べて同じぐらい難しいことが証明可能です。最初のxが秘密で
ある限り、もし公開したければ、nを公開することができます。
An intersting characteristic of this generator is that you can
directly calculate any of the s values. In particular
この生成機の面白い特徴はどのs値も直接計算できることです。特に
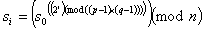
This means that in applications where many keys are generated in this
fashion, it is not necessary to save them all. Each key can be
effectively indexed and recovered from that small index and the
initial s and n.
これはこの方法で多くの鍵を生成するアプリケーションで、それらのすべて
を保存する必要がないことを意味します。各鍵に効率的にインデックスを付
け、その小さいインデックスと最初のsとnから再計算できます。
7. Key Generation Standards
7. 鍵生成標準
Several public standards are now in place for the generation of keys.
Two of these are described below. Both use DES but any equally
strong or stronger mixing function could be substituted.
いくつかの公共の標準が鍵生成ののためにあります。これらの2つが下に記
述されます。両方ともDESを使いますが、同じかより強力な混合関数が代
りに使えます。
7.1 US DoD Recommendations for Password Generation
7.1 パスワード生成の合衆国DoD推薦
The United States Department of Defense has specific recommendations
for password generation [DoD]. They suggest using the US Data
Encryption Standard [DES] in Output Feedback Mode [DES MODES] as
follows:
合衆国国防省はパスワード生成の間特定の推薦を持っています[DoD]。それ
は出力フィードバックモード[DES MODES]で次のように合衆国データ暗号化規
格[DES]を使うことを提案します:
use an initialization vector determined from
the system clock,
system ID,
user ID, and
date and time;
初期ベクトルの決定に使用するもの
システム時計、
システム識別子、
ユーザー識別子、そして
日付と時間;
use a key determined from
system interrupt registers,
system status registers, and
system counters; and,
鍵決定に使用するもの
システム割り込みレジスタ、
システム状態レジスタ、そして
システムカウンター;そして、
as plain text, use an external randomly generated 64 bit
quantity such as 8 characters typed in by a system
administrator.
普通テキストとして、システム管理者によってタイプされた
8文字のような外部でランダムに生成された64ビット量を
使ってください。
The password can then be calculated from the 64 bit "cipher text"
generated in 64-bit Output Feedback Mode. As many bits as are needed
can be taken from these 64 bits and expanded into a pronounceable
word, phrase, or other format if a human being needs to remember the
password.
パスワードは64ビット出力フィードバックモードで生成された64ビット
の「暗号文」からその時計算され得ます。必要なだけのビットがこれらの
64ビットからとる事ができて、もし人間がパスワードを覚えている必要が
あるなら、発音可能な単語や句や他のフォーマットに拡張します。
7.2 X9.17 Key Generation
7.2 X9.17鍵生成
The American National Standards Institute has specified a method for
generating a sequence of keys as follows:
米国規格協会は次のように鍵のビット列を生成する方法を指定しました:
s0 is the initial 64 bit seed
s0 は初期64ビット種です。
gn is the sequence of generated 64 bit key quantities
gn は生成された64ビット鍵の列です
k is a random key reserved for generating this key sequence
k はこの鍵列を生成するために確保したランダム鍵です
t is the time at which a key is generated to as fine a resolution
as is available (up to 64 bits).
t は可能な限りよい分解能(最高64ビット)の鍵が生成された時間です。
DES ( K, Q ) is the DES encryption of quantity Q with key K
DES ( K, Q ) は数Qを鍵KでのDES暗号化です。
gn = DES ( k, DES ( k, t ) .xor. sn )
sn+1 = DES ( k, DES ( k, t ) .xor. gn )
If g sub n is to be used as a DES key, then every eighth bit should
be adjusted for parity for that use but the entire 64 bit unmodified
g should be used in calculating the next s.
もし下付きnを伴うgがDES鍵として用いられるなら、8番目のビットがそ
の使用のためにパリティに調整されるべきですが、全部の64ビットの修正
なしのgが次のsを計算する際に使われるべきです。
8. Examples of Randomness Required
8. 必要な乱雑さの例
Below are two examples showing rough calculations of needed
randomness for security. The first is for moderate security
passwords while the second assumes a need for a very high security
cryptographic key.
以下はセキュリティに必要とされる乱雑さの荒っぽい計算を示す2つの例で
す。最初は適度なセキュリティパスワードのためです、第2が非常に高いセ
キュリティ暗号鍵の必要性を想定します。
8.1 Password Generation
8.1 パスワード生成
Assume that user passwords change once a year and it is desired that
the probability that an adversary could guess the password for a
particular account be less than one in a thousand. Further assume
that sending a password to the system is the only way to try a
password. Then the crucial question is how often an adversary can
try possibilities. Assume that delays have been introduced into a
system so that, at most, an adversary can make one password try every
six seconds. That's 600 per hour or about 15,000 per day or about
5,000,000 tries in a year. Assuming any sort of monitoring, it is
unlikely someone could actually try continuously for a year. In
fact, even if log files are only checked monthly, 500,000 tries is
more plausible before the attack is noticed and steps taken to change
passwords and make it harder to try more passwords.
ユーザーパスワードが1年1度変化し、敵が特定の口座のパスワードを推測
することができたという可能性が千分の1以下であることが望まれると想定
してください。さらにパスワードをシステムに送ることがパスワードを試み
る唯一の方法であると想定してください。それで決定的な疑問はどれぐらい
たくさん敵が試みれる可能性があるかです。敵が6秒ごとにせいぜい1つの
パスワードの試みができるように、システムに遅延導入されたと想定してく
ださい。これは毎時600で、1日におよそ15,000で、1年でおよそ
5,000,000の試みです。どんな種類のモニタリングを仮定しても、誰
かが1年間連続で実際に試みることができるとは思えません。実際、たとえ
ログファイルがただ毎月チェックするだけででも、攻撃が気付かれる前に
500,000が試みがありそうで、パスワードを変える手順でパスワードの
試みを難しくできます。
To have a one in a thousand chance of guessing the password in
500,000 tries implies a universe of at least 500,000,000 passwords or
about 2^29. Thus 29 bits of randomness are needed. This can probably
be achieved using the US DoD recommended inputs for password
generation as it has 8 inputs which probably average over 5 bits of
randomness each (see section 7.1). Using a list of 1000 words, the
password could be expressed as a three word phrase (1,000,000,000
possibilities) or, using case insensitive letters and digits, six
would suffice ((26+10)^6 = 2,176,782,336 possibilities).
500,000回の試みでパスワードを推測できるのが千分の1であるには少
なくとも全体で500,000,000種類あるいはおよそ2^29のパスワー
ドを暗示します。そのため29ビットの乱雑さが必要です。これは恐らく、
パスワード生成のために合衆国DoD推薦が平均して各5ビット以上(7.1章
参照)の乱雑さを持つ8つの入力なので、合衆国DoD推薦で遂げられることが
できます。1000の単語のリストを使って、パスワードは3つの単語句
(1,000,000,000の可能性)、あるいは、大文字小文字の違いを無
視する6つの文字と数字、((26+10)^6 = 2,176,782,336の可能性、を使って
表す事ができます。
For a higher security password, the number of bits required goes up.
To decrease the probability by 1,000 requires increasing the universe
of passwords by the same factor which adds about 10 bits. Thus to
have only a one in a million chance of a password being guessed under
the above scenario would require 39 bits of randomness and a password
that was a four word phrase from a 1000 word list or eight
letters/digits. To go to a one in 10^9 chance, 49 bits of randomness
are needed implying a five word phrase or ten letter/digit password.
より高いセキュリティパスワードで必要とされるビットの数は増加します。
可能性を千分の1に減少させるには、同様にパスワードの種類を増やすこと
が必要で、10ビットを加える必要があります。それで上記のシナリオ下で
パスワード推測が百万分の1のチャンスにするには39ビットの乱雑さが必
要で、1000の単語リストから4つの単語か、8つの文字/数字のパスワー
ドを必要とするでしょう。10^9分の1のチャンスにするには、乱雑さが
49ビット必要で5単語の句か10の文字/数字パスワードを暗示します。
In a real system, of course, there are also other factors. For
example, the larger and harder to remember passwords are, the more
likely users are to write them down resulting in an additional risk
of compromise.
本当のシステムで、もちろん、他の要因があります。例えば、大きくて思い
出すのが難しいパスワードは、ユーザがそれを書き留める可能性を増し、そ
れだ追加の危険をもたらします。
8.2 A Very High Security Cryptographic Key
8.2 非常に高セキュリティの暗号鍵
Assume that a very high security key is needed for symmetric
encryption / decryption between two parties. Assume an adversary can
observe communications and knows the algorithm being used. Within
the field of random possibilities, the adversary can try key values
in hopes of finding the one in use. Assume further that brute force
trial of keys is the best the adversary can do.
非常に高いセキュリティの鍵が2者間に対称的な暗号化/解読のために必要
と想定してください。敵が通信を観察することができ、使われているアルゴ
リズムを知っていると想定してください。ランダムな可能性のフィールドの
中で、敵は使用中の鍵を見つける試みをすることができます。さらに力づく
で鍵を試し尽くすことが敵のできる最善の方法と想定してください。
8.2.1 Effort per Key Trial
8.2.1 鍵判定毎の努力
How much effort will it take to try each key? For very high security
applications it is best to assume a low value of effort. Even if it
would clearly take tens of thousands of computer cycles or more to
try a single key, there may be some pattern that enables huge blocks
of key values to be tested with much less effort per key. Thus it is
probably best to assume no more than a couple hundred cycles per key.
(There is no clear lower bound on this as computers operate in
parallel on a number of bits and a poor encryption algorithm could
allow many keys or even groups of keys to be tested in parallel.
However, we need to assume some value and can hope that a reasonably
strong algorithm has been chosen for our hypothetical high security
task.)
それぞれの鍵を試みるにはどれぐらいの努力が必要でしょうか?非常に高い
セキュリティアプリケーションでは努力の低い値を仮定することが最も良い
です。たとえ明らかにひとつの鍵を試みるのに何万というコンピュータサイ
クルあるいはさらに多くを要するとしても、巨大な鍵ブロックを鍵毎にはる
かに少しの努力でテストできるようにするパターンがあるかもしれません。
それで鍵毎に2百サイクル以上の仮定をしないことは恐らく最も良いです。
(多くのビット上でコンピュータが並列に稼働するできるのでこれの明確な
下限がなく、そして貧しい暗号化アルゴリズムが多くの鍵あるいは鍵のグルー
プを並列にテストされることを許します。しかしながら、我々は若干の値を
仮定する必要があり、相応に強いアルゴリズムが我々の仮説の高いセキュリ
ティタスクのために選ばれたことを希望することができます。)
If the adversary can command a highly parallel processor or a large
network of work stations, 2*10^10 cycles per second is probably a
minimum assumption for availability today. Looking forward just a
couple years, there should be at least an order of magnitude
improvement. Thus assuming 10^9 keys could be checked per second or
3.6*10^11 per hour or 6*10^13 per week or 2.4*10^14 per month is
reasonable. This implies a need for a minimum of 51 bits of
randomness in keys to be sure they cannot be found in a month. Even
then it is possible that, a few years from now, a highly determined
and resourceful adversary could break the key in 2 weeks (on average
they need try only half the keys).
もし敵が超並列プロセッサや大きなワークステーションネットワークを指揮
できるなら、毎秒2*10^10サイクルが今日有効性のために恐らく最小仮定で
す。2年前と比べると少なくとも1桁の改善です。そのため毎秒10^9の、毎
時3.6*10^11、毎週6*10^13、毎月2.4*10^14の鍵が検査可能と仮定します。
これは確実にそれらが1カ月以内に見つからないためには、最小51ビット
の鍵の乱雑さの必要を暗示します。それからさえ、数年後には、固い決意の
臨機応変な敵が2週(平均して鍵の半分だけを調べる必要がある)で鍵を壊
すことができます。
8.2.2 Meet in the Middle Attacks
8.2.2 中間一致攻撃
If chosen or known plain text and the resulting encrypted text are
available, a "meet in the middle" attack is possible if the structure
of the encryption algorithm allows it. (In a known plain text
attack, the adversary knows all or part of the messages being
encrypted, possibly some standard header or trailer fields. In a
chosen plain text attack, the adversary can force some chosen plain
text to be encrypted, possibly by "leaking" an exciting text that
would then be sent by the adversary over an encrypted channel.)
もし選択あるいは既知平文と暗号文が利用可能で、暗号アルゴリズムの構造
が許すなら、「中央者」攻撃が可能です。(周知平文攻撃で、敵はすべてあ
るいは暗号化されているメッセージの一部、多分ある標準ヘッダーかトレー
ラーフィールドを知っています。選択平文攻撃で、敵はある選択平文を暗号
化させる事ができて、多分それから暗号化されたチャネル上で敵によって送
られるであろう興味のある文を「漏らす」ことができます。)
An oversimplified explanation of the meet in the middle attack is as
follows: the adversary can half-encrypt the known or chosen plain
text with all possible first half-keys, sort the output, then half-
decrypt the encoded text with all the second half-keys. If a match
is found, the full key can be assembled from the halves and used to
decrypt other parts of the message or other messages. At its best,
this type of attack can halve the exponent of the work required by
the adversary while adding a large but roughly constant factor of
effort. To be assured of safety against this, a doubling of the
amount of randomness in the key to a minimum of 102 bits is required.
中間者攻撃の単純化した説明が次の通りです:敵はすべての可能な前半鍵で
既知か選択された平文を半分暗号化して、出力を並び換え、すべての後半鍵
でそれからコード化されたテキストを半分解読することができます。もし一
致が見つかれば、半分から全部の鍵を組み立てる事ができ、他の部分や他の
メッセージの解読に使えます。最も良い場合この種の攻撃は、、一定の仕事
を増やすが、敵に必要とな仕事の指数を半減できます。これに対しする安全
性を保証するために、2倍の乱雑さの鍵、最小102ビットが必要とされま
す。
The meet in the middle attack assumes that the cryptographic
algorithm can be decomposed in this way but we can not rule that out
without a deep knowledge of the algorithm. Even if a basic algorithm
is not subject to a meet in the middle attack, an attempt to produce
a stronger algorithm by applying the basic algorithm twice (or two
different algorithms sequentially) with different keys may gain less
added security than would be expected. Such a composite algorithm
would be subject to a meet in the middle attack.
中間一致攻撃は暗号のアルゴリズムがこのように分解できることを想定しま
すが、我々はアルゴリズムの深い知識無しでこれを除外できません。たとえ
基本的なアルゴリズムが中間一致攻撃の適用を受けていないとしても、2度
基本的なアルゴリズムを(あるいは連続的に2つの異なったアルゴリズム)
適用することでより強いアルゴリズムを作り出す試みは、異なる鍵で期待さ
れるより追加のセキュリティは少ないです。このような複合アルゴリズムは
中間一致攻撃の適用を受けるでしょう。
Enormous resources may be required to mount a meet in the middle
attack but they are probably within the range of the national
security services of a major nation. Essentially all nations spy on
other nations government traffic and several nations are believed to
spy on commercial traffic for economic advantage.
巨大な資源が中間一致攻撃をするのに要求されるかもしれませんが、それら
は恐らく主要な国の国家機密サービスの射程内です。本質的にすべての国は
他国の政府トラフィックをスパイし、いくつかの国が経済の利点のために商
用トラフィックをひそかに見張ると信じられています。
8.2.3 Other Considerations
8.2.3 他の考慮
Since we have not even considered the possibilities of special
purpose code breaking hardware or just how much of a safety margin we
want beyond our assumptions above, probably a good minimum for a very
high security cryptographic key is 128 bits of randomness which
implies a minimum key length of 128 bits. If the two parties agree
on a key by Diffie-Hellman exchange [D-H], then in principle only
half of this randomness would have to be supplied by each party.
However, there is probably some correlation between their random
inputs so it is probably best to assume that each party needs to
provide at least 96 bits worth of randomness for very high security
if Diffie-Hellman is used.
我々は特別な目的のコード破壊ハードウェアの可能性を考慮した時、あるい
は上記の仮定を越えた安全性余裕を欲した時、恐らく非常に高いセキュリティ
の暗号の鍵が、最小限128ビット乱雑さで、最小鍵長は128ビットです。
もし2者がDiffie-Hellman鍵交換[DH]によって鍵を合意するなら、原則とし
てこの乱雑の2分の1をそれぞれが供給しなければならないでしょう。しか
しながら、それらのランダム入力の間に恐らく何らかの相互関係があり、も
し非常に高いセキュリティにDiffie-Hellmanが使われるなら両者がそれぞれ
少なくとも96ビットの乱雑さを提供する必要があると想定することが恐ら
く最も良いです。
This amount of randomness is beyond the limit of that in the inputs
recommended by the US DoD for password generation and could require
user typing timing, hardware random number generation, or other
sources.
この量の乱雑はパスワード生成の合衆国DoDによって勧められた入力の限界
を越えていて、ユーザータイピングタイミング、ハードウェア乱数生成、
あるいは他のソースを必要とします。
It should be noted that key length calculations such at those above
are controversial and depend on various assumptions about the
cryptographic algorithms in use. In some cases, a professional with
a deep knowledge of code breaking techniques and of the strength of
the algorithm in use could be satisfied with less than half of the
key size derived above.
上記のような鍵長計算には様々な論争があり、使用中の暗号のアルゴリズ
ムの種々な仮定に依存する事を書いておきます。ある場合には、コード破
壊技術とアルゴリズムの強さの深い知識を持つ専門家が、上記の半分以下
の鍵長で満足しています。
9. Conclusion
9. 結論
Generation of unguessable "random" secret quantities for security use
is an essential but difficult task.
予想できない「ランダム」秘密鍵生成がセキュリティに不可欠であるが、難
しい仕事です。
We have shown that hardware techniques to produce such randomness
would be relatively simple. In particular, the volume and quality
would not need to be high and existing computer hardware, such as
disk drives, can be used. Computational techniques are available to
process low quality random quantities from multiple sources or a
larger quantity of such low quality input from one source and produce
a smaller quantity of higher quality, less predictable key material.
In the absence of hardware sources of randomness, a variety of user
and software sources can frequently be used instead with care;
however, most modern systems already have hardware, such as disk
drives or audio input, that could be used to produce high quality
randomness.
我々はこのような乱雑さを作り出すハードウェアテクニックが比較的単純で
あることを示しました。特に、量と品質は高い必要がなく、ディスク・ドラ
イブのような既存のコンピュータ・ハードウェアが使えます。計算のテクニッ
クは多数のソースから低品質の乱数を、あるいは1つのソースから大量の低
品質の入力を処理して、少量の高品質で低度に予測可能な鍵材料を作り出す
ことが可能です。乱雑ハードウェアソースがない場合、いろいろなユーザー
とソフトウェアソースがしばしばその代わりに注意して使うことができます;
しかし、たいていの近代的なシステムがすでに高品質の乱雑を引き起こすた
めに使うことがでる、ディスク・ドライブや音声入力のような、ハードウェ
アを持っています。
Once a sufficient quantity of high quality seed key material (a few
hundred bits) is available, strong computational techniques are
available to produce cryptographically strong sequences of
unpredicatable quantities from this seed material.
十分な量の高品質の種鍵材料(数百ビット)が利用可能になると、強い計算
のテクニックはこの種材料から予測不能な暗号的に強い列を作るのに利用可
能です。
10. Security Considerations
10. セキュリティの考察
The entirety of this document concerns techniques and recommendations
for generating unguessable "random" quantities for use as passwords,
cryptographic keys, and similar security uses.
この文書の全部はパスワードや暗号鍵や類似のセキュリティ用とに使用する
予測できない「ランダム」生成のテクニックと推薦に関係します。
References
参考文献
[ASYMMETRIC] - Secure Communications and Asymmetric Cryptosystems,
edited by Gustavus J. Simmons, AAAS Selected Symposium 69, Westview
Press, Inc.
[BBS] - A Simple Unpredictable Pseudo-Random Number Generator, SIAM
Journal on Computing, v. 15, n. 2, 1986, L. Blum, M. Blum, & M. Shub.
[BRILLINGER] - Time Series: Data Analysis and Theory, Holden-Day,
1981, David Brillinger.
[CRC] - C.R.C. Standard Mathematical Tables, Chemical Rubber
Publishing Company.
[CRYPTO1] - Cryptography: A Primer, A Wiley-Interscience Publication,
John Wiley & Sons, 1981, Alan G. Konheim.
[CRYPTO2] - Cryptography: A New Dimension in Computer Data Security,
A Wiley-Interscience Publication, John Wiley & Sons, 1982, Carl H.
Meyer & Stephen M. Matyas.
[CRYPTO3] - Applied Cryptography: Protocols, Algorithms, and Source
Code in C, John Wiley & Sons, 1994, Bruce Schneier.
[DAVIS] - Cryptographic Randomness from Air Turbulence in Disk
Drives, Advances in Cryptology - Crypto '94, Springer-Verlag Lecture
Notes in Computer Science #839, 1984, Don Davis, Ross Ihaka, and
Philip Fenstermacher.
[DES] - Data Encryption Standard, United States of America,
Department of Commerce, National Institute of Standards and
Technology, Federal Information Processing Standard (FIPS) 46-1.
- Data Encryption Algorithm, American National Standards Institute,
ANSI X3.92-1981.
(See also FIPS 112, Password Usage, which includes FORTRAN code for
performing DES.)
[DES MODES] - DES Modes of Operation, United States of America,
Department of Commerce, National Institute of Standards and
Technology, Federal Information Processing Standard (FIPS) 81.
- Data Encryption Algorithm - Modes of Operation, American National
Standards Institute, ANSI X3.106-1983.
[D-H] - New Directions in Cryptography, IEEE Transactions on
Information Technology, November, 1976, Whitfield Diffie and Martin
E. Hellman.
[DoD] - Password Management Guideline, United States of America,
Department of Defense, Computer Security Center, CSC-STD-002-85.
(See also FIPS 112, Password Usage, which incorporates CSC-STD-002-85
as one of its appendices.)
[GIFFORD] - Natural Random Number, MIT/LCS/TM-371, September 1988,
David K. Gifford
[KNUTH] - The Art of Computer Programming, Volume 2: Seminumerical
Algorithms, Chapter 3: Random Numbers. Addison Wesley Publishing
Company, Second Edition 1982, Donald E. Knuth.
[KRAWCZYK] - How to Predict Congruential Generators, Journal of
Algorithms, V. 13, N. 4, December 1992, H. Krawczyk
[MD2] - The MD2 Message-Digest Algorithm, RFC1319, April 1992, B.
Kaliski
[MD4] - The MD4 Message-Digest Algorithm, RFC1320, April 1992, R.
Rivest
[MD5] - The MD5 Message-Digest Algorithm, RFC1321, April 1992, R.
Rivest
[PEM] - RFCs 1421 through 1424:
- RFC 1424, Privacy Enhancement for Internet Electronic Mail: Part
IV: Key Certification and Related Services, 02/10/1993, B. Kaliski
- RFC 1423, Privacy Enhancement for Internet Electronic Mail: Part
III: Algorithms, Modes, and Identifiers, 02/10/1993, D. Balenson
- RFC 1422, Privacy Enhancement for Internet Electronic Mail: Part
II: Certificate-Based Key Management, 02/10/1993, S. Kent
- RFC 1421, Privacy Enhancement for Internet Electronic Mail: Part I:
Message Encryption and Authentication Procedures, 02/10/1993, J. Linn
[SHANNON] - The Mathematical Theory of Communication, University of
Illinois Press, 1963, Claude E. Shannon. (originally from: Bell
System Technical Journal, July and October 1948)
[SHIFT1] - Shift Register Sequences, Aegean Park Press, Revised
Edition 1982, Solomon W. Golomb.
[SHIFT2] - Cryptanalysis of Shift-Register Generated Stream Cypher
Systems, Aegean Park Press, 1984, Wayne G. Barker.
[SHS] - Secure Hash Standard, United States of American, National
Institute of Science and Technology, Federal Information Processing
Standard (FIPS) 180, April 1993.
[STERN] - Secret Linear Congruential Generators are not
Cryptograhically Secure, Proceedings of IEEE STOC, 1987, J. Stern.
[VON NEUMANN] - Various techniques used in connection with random
digits, von Neumann's Collected Works, Vol. 5, Pergamon Press, 1963,
J. von Neumann.
Authors' Addresses
著者のアドレス
Donald E. Eastlake 3rd
Digital Equipment Corporation
550 King Street, LKG2-1/BB3
Littleton, MA 01460
Phone: +1 508 486 6577(w) +1 508 287 4877(h)
EMail: dee@lkg.dec.com
Stephen D. Crocker
CyberCash Inc.
2086 Hunters Crest Way
Vienna, VA 22181
Phone: +1 703-620-1222(w) +1 703-391-2651 (fax)
EMail: crocker@cybercash.com
Jeffrey I. Schiller
Massachusetts Institute of Technology
77 Massachusetts Avenue
Cambridge, MA 02139
Phone: +1 617 253 0161(w)
EMail: jis@mit.edu
Japanese translation by Ishida So