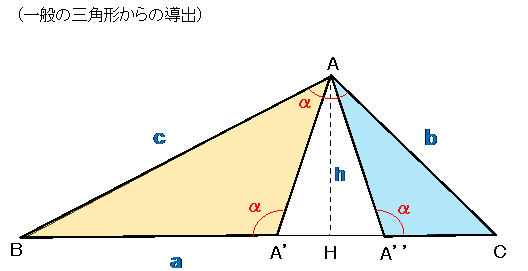
・上図は三角形の頂点Aの角度が鈍角である場合の一般三角形の図である。∠A (= α ) ≧ 90゜。
・△ABC に内接する△ABC と相似で、∠B,
∠C を共有する2つの三角形 △A’BA, △A’’AC を設定する。
点A’,A’’は外側三角形の頂点Aに対応した点であり、底辺BC上に配置される。
・△ABC ∽ △A’BA ∽ △A’’AC。で、相似比は、a:c:b = 1:(c/a):(b/a)。
・△A’AA’’は二等辺三角形で、辺AA’の長さ = b*(c/a) =(bc)/a。
底辺A’A’’の長さ = a - c*(c/a) -b*(b/a) = (a2 - b2 - c2)/a。
(∠A が鋭角の場合は、内部三角形同士は二等辺三角形の重複部を持ち、a2 - b2 - c2 の値は負。)
・すると、∠A が直角のとき、二等辺三角形はツブレて、底辺A’A’’の長さはゼロとなり、
a2 - b2 - c2 = 0 つまり、a2 = b2 + c2 が成立する。
(内側の2つの相似三角形面積の和が外側の相似三角形の面積に一致する三角形は、直角三角形に限る。)
・底辺A’A’’の長さは、2*(bc/a)*cos(π-α) = -2bc*cos(α)/a、でもある。
つまり、(a2 - b2 - c2)/a = -2bc*cos(α)/a 、が一般には成立している。
これは、a2 = b2 + c2 - 2bc*cos(α) 、なる(第二)余弦定理でもある。
■応用: ヘロンの公式(三角形の面積)
上図からだと、容易に導出可能。
三角形の高さ AH = h を a, b, c で表すと、
h2 = (AA")2 - (A''H)2 = [(bc)/a]2 - [1/2* (a2 - b2 - c2)/a]2
↓↑
(2ah)2 = (2bc)2 - (a2 - b2 - c2)2 --- ①
= (2bc + a2 - b2 - c2)*(2bc - a2 + b2 + c2) [∵ 因数分解 x2 -y2 = (x + y)*(x - y)]
= (a2 - (b - c)2)*((b + c)2 - a2)
= (a + (b - c))(a - (b - c))*((b + c) + a)((b + c) - a) = (a + b -c)(a - b + c)(a + b + c)(-a + b + c)
= (a + b + c)(-a + b + c)(a - b + c)(a + b -c)
↓↑
2ah = ± SQRT ((a + b + c)(-a + b + c)(a - b + c)(a + b -c))
よって、面積 = (1/2)ah = (1/4)*SQRT [(a + b + c)(-a + b + c)(a - b + c)(a + b -c)]
【易しい因数分解の練習問題でした。昔の高一レベル。】
c. 補足:①の式を良く見るとは、b, c 対称。また、a2 - b2 - c2 は、a2 - (b ± c)2 ± 2bc なので、
a2 - (b ± c)2 = 0 のとき、①全体は、(2bc)2 - (±2bc)2 でゼロ。
なので、①の式は、a2 - (b ± c)2 = (a + (b ± c))*(a - (b ± c)) を因数に持つことが予測できる。【因数定理です】。