§Algorithm§

☆二等分割法☆

　コンピューター計算で、
x^2 + 5x -6 = 0
x^3 + x^2 + x -5 = 0
x^4 + 2x^3 + x^2 + 3x -2 = 0
のような非線形方程式を如何にして解くか？ コンピューターは、ひらめきを有する因数分解を 非常に苦手としているので、独自の計算方法が用いられます。 ここでは、そのうちの１つの二等分割法について解説してあります。

　例えば、x^3 + x^2 + x -5 = 0 の実数解は、y = x^3 + x^2 + x -5 の非線形図形、 次の図のような x 軸との交点と考えることができます。

　そこで、この値を挟む x の値をそれぞれ high,low として、その値に対しての yh,yl 値を求めます。ここでは、交点を挟んでいるわけですから、 yh ＞ 0,yl ＜ 0 となります。

　次に、high,low の中間点である x = mid1 = (high + low) / 2 を求め、 その mid1 値に対しても ym 値を求めます。そしてその ym の符号が正であるか 負であるかによって、mid1を新しい low,high 値にするかを決めます。下の図 では、ym が負であるので low = mid1 と代入し、またその中間点を求め・・・ というように徐々に解の範囲を狭めて、収束した点を解とします。

この二等分割法、Visual Basicのプログラムコードでは以下のようにまとめられます。
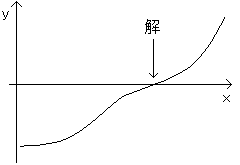
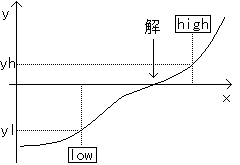
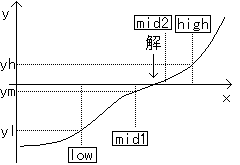
−注意−
下のコードではサンプルプログラムに合わせるために、y値の代入に 引数に指定された式データを用いていますが、実際はlogやCosやSinなどを用いた方程式も 多いかと思います。その都度、コードを変更してお使い下さい。 

'===========================================================
'Bunkatsu   二等分割法により非線形方程式を解く
'---------引数----------------------------------------------
'nc：次元数
'cValue()：式データ(cValue(0)=2,cValue(1)=1の場合、2+x^2=0)
'limit：ループ回数の限界値
'neZero：解はy=0の時であるが、それをy＜Abs(neZero)にすること
'high：解が存在する可能性のある最大値
'low：解が存在する可能性のある最小値
'---------戻り値--------------------------------------------
'解を返すが、解が得られなかった時は0.0を返す
'===========================================================
Public Function Bunkatsu(nc As Long, cValue() As Double, _
                    limit As Long, neZero As Double, _
                    high As Double, low As Double) As Double
    'xである high と mid を代入したときの値、midは(high+low)/2
    Dim y0 As Double, y1 As Double, mid As Double
    Dim i As Long, j As Long 'カウンタ
    i = 0& '初期化
    For i = 0& To limit - 1&
        y1 = 0#: y0 = 0# '初期化
        mid = (high + low) / 2# '解である可能性の範囲を狭める
        '引数に指定された式データからy値を求める
        'このy=0である時、その high or mid の値が解となる
        For j = 0& To nc
            y1 = y1 + cValue(j) * (mid ^ j)
            y0 = y0 + cValue(j) * (high ^ j)
        Next j
        'y0 と y1 の符号が常に違うようにする
        If (y0 * y1) > 0# Then
            high = mid
        Else
            low = mid
        End If
        '誤差の値以下(y の値がnearly=0)ならそれを解とする
        If Abs(y0) < Abs(neZero) Then
            Bunkatsu = high: Exit Function
        End If
        If Abs(y1) < Abs(neZero) Then
            Bunkatsu = mid: Exit Function
        End If
    Next i
    'このプロシージャでは、0.0 を解とするものをエラーと考える
    Bunkatsu = 0# '収束しなかった時
End Function

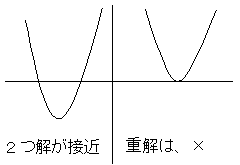
　この方法は、解を挟んだy値の符号で判断するので、解がある程度予測され なければなりません。（通常、その予測には試行法と呼ばれる方法を用います） そのため、余計な計算の手間がかかる上に、狭い範囲に２つ以上の解がある 場合や解が重解である場合は、正確に計算できない場合が多いという欠点があります。
　従って３次元方程式の解を求める、科学や化学的な計算には有効な方法ですが、 解の範囲が予測不可能で、多重の実数解があるものには、有効であるとは 言えません。例えば、次のような二次方程式の場合もそうです。左側は、あまりに２つの解が接近しており 解範囲が特定しにくく、右側は重解で、y値の符号は常に正なので、解を求めることができません。

（サンプルプログラムの動作確認）

機種 PC-9821V13S
OS Windows95
開発ツール Visual Basic Ver.4.0
更新日 00/4/15

ダウンロード Bunkatsu.lzh(2.70KB)

Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で起きた損害などに関して一切の責任を負うことはできません。

★このコーナーに掲載されているプログラムコード、およびプログラムファ イルを無断で配布・転載することは、原則として禁止です。

Algorithmインデックス トップ

Copyright(C)2000 Tomoya. All rights reserved.