|
*** (今回のサンプルはあくまで理論の追求を目的としました。ので、実際にこういう方法が 用いられることはあまりないと思います。(^^)) *** 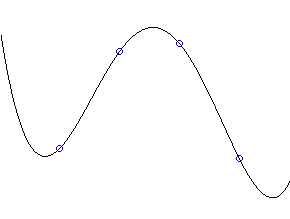 もし、与えられた点が2つならば、それは直線になり、 y = a * x + b のように1次式で表せます。 同様にして点が3つならば、 y = a * x^2 + b * x + c のように2次式で表せます。 そこで、次のように定義することができます。
点が3つあるとします。 これらの点を通る曲線は y = a * x^2 + b * x + c と表せ、3点を(x1,y1),(x2,y2),(x3,y3)とすれば、 a * x1^2 + b * x1 + c = y1 a * x2^2 + b * x2 + c = y2 a * x3^2 + b * x3 + c = y3 というように3つの式が成り立ちます。 未知数である係数が a,b,c の3つなので、 これらは解くことができます。 そこで以前紹介したガウス・ジョルダン法でこの連立方程式を解いてやれば、 求めたい曲線の方程式が得られます。 その計算方法については下のサンプルコードを見て下さい。 (例によって行と列が逆になっています。気になる方は修正して下さい。(^^)) 得られた式に、x を代入して y を求め1点1点直線で結んでやれば、 曲線も描くことができます。 しかしこの方法では、点の数が多くなればなるほどべき乗回数が 多くなり効率的とは言えませんし、浮動小数点の記憶できる範囲により正確に 計算できない事もあります。 与えられる x の範囲にもよりますが、 点の数が10個ぐらいが限界でしょうか・・・。 その他でも多項式補間の定石的方法として、ラグランジュ補間やニュートン補間等がありますが、 点の数が多い場合は、多項式補間ではないスプライン補間を用いるのが一般的です。 |
Public Type POINT
x As Double
y As Double
End Type
'GaussJordan ガウス−ジョルダン法で連立方程式を解く
'詳しくはそのサンプルをご覧下さい
Private Function GaussJordan(value() As Double, _
count As Long) As Boolean
Dim a As Double
Dim i As Long, j As Long
Dim k As Long
Dim temp As Double
For i = 0& To count - 1&
a = value(i, i)
If Abs(a) < 0.0001 Then GaussJordan = False: Exit Function
For k = i To count
value(k, i) = value(k, i) / a
Next k
For j = 0& To count - 1&
If j <> i Then
temp = value(i, j)
For k = i To count
value(k, j) = value(k, j) - _
temp * value(k, i)
Next k
End If
Next j
Next i
GaussJordan = True
End Function
'与えられた点をすべて通る曲線を描く
'実用性はありません・・・
'pos() 点
'pCount 点の数
'sPic 描画先ピクチャボックス
'sx,ex 描画開始,終了位置
Public Function DrawCarveLine(pos() As POINT, _
ByVal pCount As Long, _
ByVal sPic As Object, _
ByVal sx As Long, _
ByVal ex As Long)
Dim gj() As Double '連立方程式を解くための行列の値
Dim i As Long, j As Long 'カウンタ
ReDim gj(pCount - 1 + 1, pCount - 1) '[点の数]の正方行列
'点のx,y値を連立方程式を解くための行列値にする
For j = 0& To pCount - 1&
For i = 0& To pCount - 1&
gj(i, j) = pos(j).x ^ (pCount - 1 - i)
Next i
gj(pCount, j) = pos(j).y
Next j
'連立方程式を解く
If GaussJordan(gj, pCount) = False Then Exit Function
Dim y As Double '補間された値
Dim tempx As Double, tempy As Double '点と点を結ぶための補間変数
tempx = 0#: tempy = 0#
'座標スケールの定義
sPic.Scale (0, sPic.Height)-(sPic.Width, 0)
'連立方程式の解を使用して補間値を求め曲線を描く
For j = sx To ex
y = 0#
For i = 0& To pCount - 1&
y = y + (j ^ (pCount - 1 - i)) * gj(pCount, i)
Next i
If j <> sx Then sPic.Line (tempx, tempy)-(j, y)
tempx = j: tempy = y
Next j
End Function
|
Private Const POS_C = 5&
Private Sub Command1_Click()
Dim p(POS_C - 1) As POINT
Dim i As Long
Picture1.Cls
Picture1.Scale (0, Picture1.Height)-(Picture1.Width, 0)
For i = 0 To POS_C - 1
p(i).x = CDbl((i + 1) * Picture1.Width / POS_C)
p(i).y = Int(Picture1.Height * Rnd)
Picture1.Circle (p(i).x, p(i).y), 3, RGB(0, 0, 255)
Next i
Call DrawCarveLine(p, POS_C, Picture1, 0, Picture1.Width)
End Sub
|
| (ミニ知識) こういったすべての点を通る曲線は、測定誤差が必ず生じる 化学分析などではめったに使われません。 |
| 機種 | PC-9821V13S |
| OS | Windows95 |
| 開発ツール | Visual Basic Ver.4.0 |
| 更新日 | 00/12/31 |
Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で生じた損害などに関して一切の責任を負うことはできません。
★掲載されているプログラムコード、およびプログラムファイル、 ソースファイルを無断で配布・転載することは、原則として禁止です。