§Algorithm§

☆連立方程式の解−ガウス・ジョルダン法−☆

次のような未知数が2つの２元連立方程式ならば、

2a + 3b = 12
5a + 2b = 19

2つの式からa,bのどちらかを消去して、a=3,b=2を導き出せます。
では、未知数が3つだったら？

2a + 2b + 3c = 15
3a + 5b + 2c = 19
5a + 3b + 3c = 20

ちょっとややこしくなりますが、これも同様な計算方法で、 a=1,b=2,c=3を導き出すことができます。
さらに未知数が増えて4つでは？
・・・もはや、消去→代入法の計算方法では限界があります。
そのような多元連立方程式をどのように解くか？
ここでは、その一番シンプルな解法を紹介しています。
 


  上記の3元連立方程式を例に取り進めていきます。

2a + 2b + 3c = 15 --- (1)
3a + 5b + 2c = 19 --- (2)
5a + 3b + 3c = 20 --- (3)

の解は、a=1,b=2,c=3ですが、
これは次のように表すこともできます。

1a + 0b + 0c = 1 --- (1)'
0a + 1b + 0c = 2 --- (2)'
0a + 0b + 1c = 3 --- (3)'

  そうすると、もし上の式から下の式に変換することが
できるならば、解を求められるわけです。

  では、どのように変換するか？、ですが、
以下のような流れで行います。
  まず、(1)式の未知数 a の係数 = 2を 1 にする
ために、(1)式(注目式)全体をその係数 = 2で割ります。

1a + 1b + (3/2)c = 15/2 --- (1.1)

  次に、注目式以外の(2),(3)式の a の係数
を 0 にします。

(2.1) = (2) - (1.1) * 3
(3.1) = (3) - (1.1) * 5

ここで、一旦式を見てみると、

1a +    1b +  (3/2)c = 15/2  --- (1.1)
0a +    2b + (-5/2)c = -7/2  --- (2.1)
0a + (-2)b + (-9/2)c = -35/2 --- (3.1)

  次に、(2.1)式の未知数bの係数を 1 にするために、
(2.1)式(注目式)全体をその係数 = 2で割ります。

0a + 1b + (-5/4)c = -7/4 --- (2.2)

  先程同様に注目式以外の
(1.1),(3.1)式の b の係数を 0 にします。

(1.2) = (1.1) - (2.2) * 1
(3.2) = (3.1) - (2.2) * -2

  ここまでで、式は次のようになっています。

1a + 0b + (11/4)c = 37/4  --- (1.2)
0a + 1b + (-5/4)c = -7/4  --- (2.2)
0a + 0b +   (-7)c = -21   --- (3.2)

  (3.2)式の未知数 c の係数を 1 にするために、
(3.2)式(注目式)全体をその係数 = -7で割ります。

0a + 0b + 1c = 3 --- (3)'

最後に、注目式以外の
(1.2),(2.2)式の c の係数を 0 にします。

(1)' = (1.2) - (3.2)* 11/4
(2)' = (2.2) - (3.2)* -5/4

計算終了です。未知数がいくら増えても、
それに対応する式があれば(未知数の数＝式の数)、
同様の手法で計算可能です。

1a + 0b + 0c = 1 --- (1)'
0a + 1b + 0c = 2 --- (2)'
0a + 0b + 1c = 3 --- (3)'

なかなかややこしいですが、コード的には次のようにまとめられます。 

'===========================================================
'GaussJordan  ガウス−ジョルダン法で連立方程式を解く、
'             解は、最終列に格納する
'---------引数----------------------------------------------
'value()     2次元の配列(最初の次元が横、次が縦の係数)
'count       ？元連立方程式であるか（？行？列の正方行列）
'---------戻り値--------------------------------------------
'方程式が解ければTrueを返し、そうでなければFalseを返す(0除算)
'===========================================================
Public Function GaussJordan(value() As Double, _
                            count As Long) As Boolean
    Dim a As Double          '注目式の未知数の係数
    Dim i As Long, j As Long '縦の係数操作のためのカウンタ
    Dim k As Long            '横の係数操作のためのカウンタ
    Dim temp As Double       '注目式以外の未知数の係数
    
    '1つ目の未知数から、順に処理していく(上から下へ)
    For i = 0& To count - 1&
        
        '注目式の未知数の係数を1にするためにその係数を格納
        a = value(i, i)
        
        '0除算、オーバーフロー除け
        If Abs(a) < 0.0001 Then GaussJordan = False: Exit Function
        
        '注目式の未知数の係数を1にするため注目式全体をaで割る
        For k = i To count
            value(k, i) = value(k, i) / a
        Next k
        
        '注目式以外の未知数の係数を0にする
        For j = 0& To count - 1&
            '注目式以外なら実行する
            If j <> i Then
                '注目式以外の未知数の係数を格納
                temp = value(i, j)
                'その値を0にするため、注目式との演算を行う
                For k = i To count
                    value(k, j) = value(k, j) - _
                                  temp * value(k, i)
                Next k
            End If
        Next j
    Next i
    GaussJordan = True
End Function

0除算による計算中断がこの計算方法の最大の欠点です。

この上記の方法は、通常『行列』を使って考えられており、 上の2つの連立方程式を行列に置き換えると、次のように表せます。

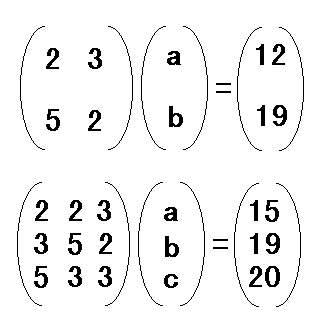
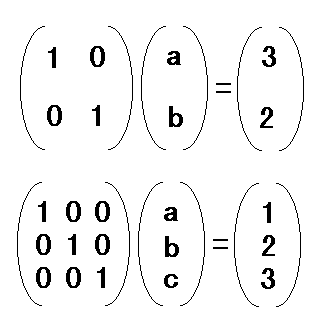
また、この行列式で2つの式の解を表すと、次のようになります。 右側の値が解です。

この式、斜めに1ばかりで、その他は0の行列を『単位行列』といいます。 この単位行列に何をかけても、元の値のままで変化しません。つまり、 一般の計算式の1にあたります。・・・で、 もし、上の方程式の行列式(左側)部分を 下の解の行列式(単位行列)に変換することができるならば、解を 求められることになります。 「それじゃあ、無理矢理1と0にしちゃえー」、というのが行列を使った 連立方程式の解き方で、上で説明したものをより数学的に表したものです。

こういう行列的な計算方法は、Excelで視覚的に計算課程を見ていく方が 遙かにわかりやすいです。ExcelでのサンプルもUPしておきましたので、 よろしければダウンロードしてみて下さい。

（サンプルプログラムの動作確認）

機種 PC-9821V13S
OS Windows95
開発ツール Visual Basic Ver.4.0(ソース)
Excel 97(ワークシート)
更新日 00/5/21

ソースファイル GaussJ.lzh(3.58KB)

ワークシート excelG.lzh(5.86KB)

Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で起きた損害などに関して一切の責任を負うことはできません。

★このコーナーに掲載されているプログラムコード、およびプログラムファ イルを無断で配布・転載することは、原則として禁止です。

Algorithmインデックス トップ

Copyright(C)2000 Tomoya. All rights reserved.