|
ここでは、線分交差判定の定石ともいえる方法を紹介しています。 線分と直線の見落としがちな大切な定義です。 |
|
直線とは、ある2点を通る線であり、 線分とは、ある2点を結ぶ線である。 |
|
交差判定について、
点A,B,C,D、線分ABと線分CDの交差について考えていきます。
まず、『線分の交差判定』における
従来の 「交点を求め、その交点が2つの線分の範囲にあるかを調べる」 という考え方を別の解釈に置き換えます。 2線分が交差しているということは、 点C,Dを通る直線が線分ABと交差している」 と解釈できます。そこで、直線と線分の交差は次のように判定します。 直線に対して両側に存在するとき、直線と線分は交差する」 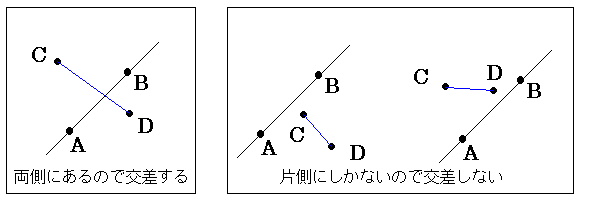 y=ax+bという直線と、=を不等号に置き換えた y>ax+b、y<ax+b という領域を示す式があったとすれば、 これら3つの式が描く図形、領域は次のように示せます。 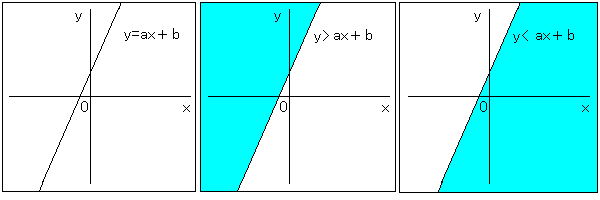 y-ax-b<0 とすることができます。 ある点が直線に対してどちらの 側にあるかを求めたい場合、直線の方程式にその点の(X,Y)を代入し、 結果得られた値が正であるか負であるかによって、知ることができます。 正であれば、ある点は直線の上の部分に、負であれば、 ある点は直線の下の部分に、位置するということがわかります。 直線の両側(上側と下側)に点があれば交差するので、 直線と線分の交差判定を行うには、 線分を構成する2つの点を直線の方程式に代入し、得られた値の 符号がお互い異なる(もしくは0)かどうかを調べればいいわけです。 異なっていれば(互いをかけた数<0)、交差していると判定できます。 このことを具体的に式化してみます。 点A,Bの座標を A(x1,y1),B(x2,y2) として、この2点を通る直線と 点C,Dの座標、 C(x3,y3),D(x4,y4) を結ぶ線分について考えます。 点A(x1,y1),B(x2,y2)を通る直線ABの方程式は、 と表せます。割り算は0除算やオーバーフローが怖いため避けるので、 両辺に(x1-x2)をかけ、次のように変形します。 これをさらに簡略化して、左辺に集めます。 これが、点A(x1,y1),B(x2,y2)を通る直線の方程式です。 ここで、この方程式に点C(x3,y3),D(x4,y4)を代入し、その符号を調べることによって 直線と線分の交差判定ができます。 点Cを代入 交差する=2つの式の符号が異なる、ということを式で表すと、 のようになり、以下のコードで判定可能です。 プロシージャにすると、1行ではないですが、 考え方自体は、One Line です。 |
'構造体
Private Type POINT
x As Double
y As Double
End Type
'座標 p1,p2 を通る直線と座標 p3,p4 を結ぶ線分が交差しているかを調べる
Private Function intersect(p1 As POINT, p2 As POINT, p3 As POINT, p4 As POINT) as Boolean
If (((p1.x - p2.x) * (p3.y - p1.y) + (p1.y - p2.y) * (p1.x - p3.x)) * _
((p1.x - p2.x) * (p4.y - p1.y) + (p1.y - p2.y) * (p1.x - p4.x)) > 0#) Then
'交差しない
intersect = False
Exit Function
End If
'交差する
intersect = True
End Function
|
|
そして、線分ABと直線CDについても同様の計算を用いて、 tb=(x3-x4)*(y2-y3)+(y3-y4)*(x3-x2) ta*tb<0 上記のものとあわせて、2つの条件判定すれば、2つの線分の交差判定を行うことができます。 |
'構造体
Private Type POINT
x As Double
y As Double
End Type
'座標 p1,p2 を結ぶ線分と座標 p3,p4 を結ぶ線分が交差しているかを調べる
'ただし、線分が重なっている場合(3点,4点が一直線上にある)、「交差していない」、と判定します。
Private Function intersection(p1 As POINT, p2 As POINT, p3 As POINT, p4 As POINT) as Boolean
If (((p1.x - p2.x) * (p3.y - p1.y) + (p1.y - p2.y) * (p1.x - p3.x)) * _
((p1.x - p2.x) * (p4.y - p1.y) + (p1.y - p2.y) * (p1.x - p4.x)) < 0#) Then
If (((p3.x - p4.x) * (p1.y - p3.y) + (p3.y - p4.y) * (p3.x - p1.x)) * _
((p3.x - p4.x) * (p2.y - p3.y) + (p3.y - p4.y) * (p3.x - p2.x)) < 0#) Then
intersection = True
Exit Function
End If
End If
intersection = False
End Function
|
|
この判定では、線分同士が重なっている場合(3点あるいは4点が一直線上にある)、「交差していない」、と判定します。
これを「交差する」と判定したい場合については、もっと高速に−線分交差判定−をご覧下さい。
上のアルゴリズムだけでは、これを判定するのはちょっと難しいです・・・。 (乗算によるオーバーフローと整数と浮動小数点) 上のコードは、浮動小数点の演算で行っていますが、実際にこの処理を Windowsの描画などで使用する場合は整数計算のみで可能ですし、 浮動小数点ではなく、Long型の整数を使用した方が高速に処理できます から、そちらの方がいいかもしれません。 もし、判定したい線分の点が とんでもなく大きい場合、乗算によるオーバーフローが懸念されるので、 全体のスケール自体を小さくし、浮動小数点にして計算を行う必要があります。 そんなとき、宣言する変数を変更するだけで利用できるこの計算方法は 非常に便利で優れていると思います。 下のサンプルでは、整数版を使用しています。 (参考までに・・・) 大抵の参考書では、この交差判定を、 「点A,Bを通る直線とある点Cの位置関係について、ABCの順に追って 点が時計回り、あるいは反時計回りに位置しているか、ということを知り・・・、」 というように記述して解説されていると思います。上の説明は、この方法を 証明形式に行ってみました。 (参考書) 『アルゴリズムC 第3巻』 野平浩平、星守、佐藤創、田口東 共訳 近代科学社 『アルゴリズムとデータ構造』 江村潤朗、上坂吉則、浅井宗海、有澤誠、西村俊介 実教出版 |
| 機種 | PC-9821V13S |
| OS | Windows95 |
| 開発ツール | Visual Basic Ver.4.0 |
| 更新日 | 00/07/22 |
Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で生じた損害などに関して一切の責任を負うことはできません。
★この線分交差は色々な処理で使用できると思います。 本ソース文書の配布・転載は禁止ですが、掲載されているプログラムコード、 およびプログラムファイルについては、各自の責任においてご自由に配布して もらって構いません。その時、本サイトを紹介していただけると非常にうれしいです。