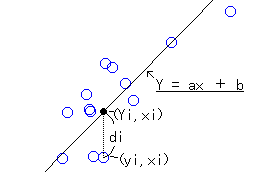§Algorithm§

☆最小二乗法による回帰直線☆

実験データの分析に良く用いられる回帰直線(近似直線)の理論は比較的簡単です。 順に見ていきましょう。

(直線回帰させることの意義)

　ある実験で、何らかの要因が他の要因とどれだけ関わりがあるかを調べる 時、その2つの要因を(x,y)としてとり、グラフ化してやると一目でその傾向が 分かります。(身近な物で言うと、人の身長と体重かな・・・。) また、そのプロットに対して直線や曲線を引くことができれば、 それを式にする事もできるので、統計分析の幅も広がります。
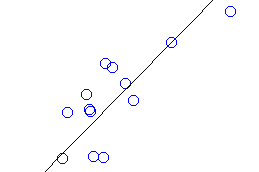　ある実験結果をグラフプロットし、そのプロットに対して 近似直線を引くことは、 その実験結果をy=ax+bの形の式で表せることにもなります。 そしてその式を用いて x にある値を代入すれば未知のyを求めることができ(その逆も)、 度々実験をしなくてもある程度の予測をつけることができます。 これは当然と言えば当然なのですが科学的には非常に 重要なことです。
　学校の教科書に出てくる公式は、偉ーい学者さんたちが何度も 実験→プロット→統計分析して得られた結果なわけですね。 公式は、当然1次のものばかりではありませんが、 「公式はシンプルであるべし」（勝手な持論です(^^)）

(直線回帰理論)

上図のように点在したプロットに対して、ある直線を引くとします。
そこで、この直線がそれらの点の分散と限りなく一致している時、
回帰直線となります。例えば、
Y = ax + bとプロット値(xi,yi)[i=0〜n]ついて考えてみます。

Y0 - y0 = ax0 + b - y0 = 0
Y1 - y1 = ax1 + b - y1 = 0
：
Yn - yn = axn + b - yn = 0

であれば、プロット値は直線に完全に乗っています。でも実際の実験等では
誤差が生じているはずなので、

Y0 - y0 = ax0 + b - y0 = d0
Y1 - y1 = ax1 + b - y1 = d1
：
Yn - yn = axn + b - yn = dn

となります。


この、誤差の二乗の合計(Yi と yiの距離の二乗の合計)

s = d0^2 + d1^2 +・・・+ dn^2

が最小になるような係数a,bを求めれば、散在した点の回帰直線を引くことができます。
(最小二乗法)

(直線の方程式の係数 a,b の求め方)

その合計を式で表すと、
(シグマが文字化けしていたらごめんなさい)

s = (yi - axi - b)^2 [i=0〜n]

となり、これを展開して

s = (yi^2 + a^2 * xi^2 + b^2 - 2yi * axi - 2yi * b + 2axi * b)

次に、a,bを求めるために、これをa,bでそれぞれ微分します。
aで微分して

ds / da = 2xi(a * xi - yi + b) = 0
2a * (xi^2) - 2 * (x1 * y1) + 2b * 肺i = 0 --- (1)

bで微分して

ds / db = 2 * (b - yi + axi) = 0
2nb - 2 * 輩i + 2a * 肺i = 0 ---(2)

(1),(2)式より、

a = ((xi * yi) - b * 肺i) / (xi^2)
b = (輩i - a * 肺i) / n

2式を解いて、

a = ((xi * yi) - (肺i * 輩i) / n) / ((xi^2) - (肺i * 肺i) / n)

これにより、実験データx,yから、係数a,bが求められます。



Public Const MAX_X = 300
Public Const MAX_Y = 300
Public Const MIN_X = 0
Public Const MIN_Y = 0
Public Const PLOT_COUNT = 30
Public Const PLOT_CIRCLE_RADIUS = 2
Public Const PLOT_CIRCLE_COLOR = &HFF0000
Public Type POINT
    x As Long
    y As Long
End Type
Public plot_data(PLOT_COUNT - 1) As POINT

'プロットデータを作成する
'ここでは、y=xの近似直線を引くようにする
Public Sub SetPlotData(ByVal sList As Object, _
                        ByVal sPic As Object)
    
    Dim i As Long, t As Long
    sList.Clear
    sPic.Cls
    Randomize
    sPic.Scale (MIN_X, MAX_Y)-(MAX_X, MIN_Y)
    For i = 0 To PLOT_COUNT - 1
        plot_data(i).x = Int(Rnd * MAX_X)
        plot_data(i).y = plot_data(i).x + (Int(Rnd * MAX_Y - MAX_Y \ 2)) \ 3
        sList.AddItem plot_data(i).x & "," & plot_data(i).y
        sPic.Circle (plot_data(i).x, plot_data(i).y), _
                   PLOT_CIRCLE_RADIUS, PLOT_CIRCLE_COLOR
    Next i
    
End Sub

'xの総和を求める
Public Function GetSumX() As Double

    Dim SumValue As Double
    Dim i As Integer
    SumValue = 0#
    For i = 0 To PLOT_COUNT - 1
        SumValue = SumValue + plot_data(i).x
    Next i
    GetSumX = SumValue

End Function

'yの総和を求める
Public Function GetSumY() As Double

    Dim SumValue As Double
    Dim i As Integer
    SumValue = 0#
    For i = 0 To PLOT_COUNT - 1
        SumValue = SumValue + plot_data(i).y
    Next i
    GetSumY = SumValue

End Function

'xを2乗した値の総和を求める
Public Function GetSumSpaX() As Double
    
    Dim SumSpaValue As Double
    Dim i As Integer
    SumSpaValue = 0#
    For i = 0 To PLOT_COUNT - 1
        SumSpaValue = SumSpaValue + plot_data(i).x ^ 2#
    Next i
    GetSumSpaX = SumSpaValue

End Function

'yを2乗した値の総和を求める
Public Function GetSumSpaY() As Double
    
    Dim SumSpaValue As Double
    Dim i As Integer
    SumSpaValue = 0#
    For i = 0 To PLOT_COUNT - 1
        SumSpaValue = SumSpaValue + plot_data(i).y ^ 2#
    Next i
    GetSumSpaY = SumSpaValue

End Function

'xとyの積和を求める
Public Function GetSumMul() As Double
    
    Dim i As Long
    Dim SumMulValue As Double
    SumMulValue = 0#
    For i = 0& To PLOT_COUNT - 1&
        SumMulValue = SumMulValue + plot_data(i).x * plot_data(i).y
    Next i
    GetSumMul = SumMulValue
    
End Function

'回帰直線を描画し、相関係数を戻り値として返す
Public Function DrawLinearFit(ByVal sPic As Object) As Double

    Dim sx As Double, sy As Double, sm As Double
    Dim sxp As Double, syp As Double
    Dim a As Double, b As Double
    sx = GetSumX
    sy = GetSumY
    sxp = GetSumSpaX
    syp = GetSumSpaY
    sm = GetSumMul
    a = (sm - sx * sy / PLOT_COUNT) / _
        (sxp - sx * sx / PLOT_COUNT)
    b = (sy - a * sx) / PLOT_COUNT
    sPic.Line (MIN_X, MIN_X * a + b)-(MAX_X, MAX_X * a + b)
    DrawLinearFit = (sm - sx * sy / PLOT_COUNT) / _
                      Sqr(sxp - sx * sx / PLOT_COUNT) / _
                      Sqr(syp - sy * sy / PLOT_COUNT)
    
End Function

相関係数は、↑のような感じで求めることができますが、この値が 1に近いほど、x,y がより深い関係があることになります。

（参考書）
『アルゴリズム演習300題』
著者： 橋本英美氏
出版元：日刊工業新聞社

（サンプルプログラムの動作確認）

機種 PC-9821V13S
OS Windows95
開発ツール Visual Basic Ver.4.0
更新日 00/12/25

ダウンロード Linear.lzh(2.51KB)

Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で生じた損害などに関して一切の責任を負うことはできません。

★掲載されているプログラムコード、およびプログラムファイル、 ソースファイルを無断で配布・転載することは、原則として禁止です。

Algorithmインデックス トップ

Copyright(C)2000 Tomoya. All rights reserved.