☆積分−役に立つ?−☆
「f(x) = x^2 、これを積分しろ」ぐらいなら、
∫f(x)dx = (x^3) / 3 + C
ってな感じでわかるんだけど、ちょっと複雑になると、 さっぱりわからなくなります。ここには、そんな積分恐怖症の僕から見た 『積分論』を記してあります。(^^
まず、こんな『積分』が役に立つのか?今でも「役にたたん!」と強がって おりますが、実際は、僕のような工学系の者が知らないとかなりまずいようです。 「数学の専門家さんなら当然勉強して価値があるものだろうけど、僕のように?? が専門であれば、あまり必要ないだろう。」のような楽観主義だったんですが、 数学以外の科目でも、この忌まわしき『積分』がでるわでるわの大盛況で、 テストの度に苦い思いをしました。
そのバーゲンセールのごとき『積分』の使われ方ですが、多くが 何らかの計算値を求めるための公式などに目立ちました。つまり、定積分ですね。 ←は当然のことなんですけど、ここがポイントで、研究などで必要なのであれば、 要するにこの積分を使わずに計算値さえ求めればいいわけです。 それじゃ、積分を使わずにその定積分をどうやって求めるか? (関数電卓で求めれたっけ?、こんなことも忘れてしまった・・・。)
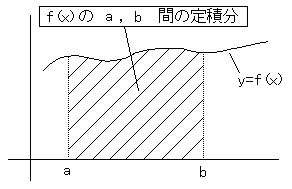
定積分を求めることは、曲線とx軸で囲まれた部分の面積を 求めることと同じ事です。例えば、y=f(x)、を x=a,x=b 間で定積分を行うと、 曲線 y=f(x)と直線 x=a,x=b で囲まれた部分の面積を求めることができます。 (もちろん、あくまで仮定的な面積なので、負になることもあります。)
・・・といっても、テストではどうしようもないですけどね。(^^
結論として、積分は工学系の研究者を目指す方なら知っている方 がかなり有利になりますし、他の分野の理解度がより深まると思います。 (積分を用いると、グラフプロットで曲線を直線化できたりするところが結構重要ですね。>実験) 僕はもう手遅れですけどね。経験者の一言です。
「やはり、ちゃんと勉強することが1番です。」(^^