§Algorithm§

☆三角形と多角形の面積☆

　「三角形は、原点Oとある線分ABによって作成される図形」と定義できます。 そこで、三角形OABの面積は、

(原点Oと直線ABとの距離OH) * (線分ABの長さ) / 2

であると、考える事ができます。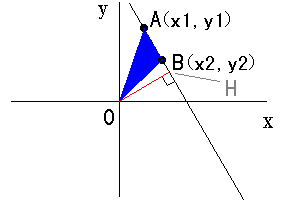

　詳しく見ていきます。
ある点P(Px,Py)と直線の距離PHは、直線の式を ax+by+c=0 とすると、

PH = Abs(a*Px + b*Py + c) / Sqr(a^2 + b^2)

と表せます。また、点Pが原点O(0,0)であれば、この式は、

OH = Abs(c) / Sqr(a^2 + b^2)

と簡略化できます。
　一方、A(x1,y1),B(x2,y2)とすれば、線分ABの長さは

AB = Sqr((y2-y1)^2+(x2-x1)^2)

と表せ、直線ABの方程式は、

(x1-x2) * (y-y1) - (y1-y2) * (x-x1) = 0

と示せるので、これを ax+by+c=0 の形にするために x,yでまとめると、

x(y2-y1) - y(x2-x1) + x2*y1 - x1*y2 = 0

となり、この式では、a = (y2-y1),b = -(x2-x1),c = x2*y1 - x1*y2　であり、
この直線と原点の距離は、

OH = Abs(x2*y1 - x1*y2) / sqr((y2-y1)^2 + (-(x2-x1))^2)

と示せます。[-] を消去して

OH = Abs(x2*y1 - x1*y2) / sqr((y2-y1)^2 + (x2-x1)^2)

とすることができます。
三角形OABの面積は、
sOAB = (原点Oと直線ABとの距離)*(線分ABの長さ) / 2
と表せたので、
(原点Oと直線ABの距離) = Abs(x2*y1 - x1*y2) / sqr((y2-y1)^2 + (x2-x1)^2)
(線分ABの長さ) = sqr((y2-y1)^2+(x2-x1)^2)
をそれぞれ代入して計算すると、

原点Oと線分ABで囲まれる三角形の面積
sOAB = Abs(x2*y1 - x1*y2) / 2

とシンプルな式で表すことができます。

高校数学でよく見かけるこの式、もしや線分交差判定の式では・・・。(^^
 


'座標(px1,py1)と(px2,py2)を結ぶ線分と原点によって囲まれる
'三角形の面積を求める
Public Function GetTriSurfaceArea(ByVal px1 As Double, _
                                  ByVal py1 As Double, _
                                  ByVal px2 As Double, _
                                  ByVal py2 As Double) As Double
    GetTriSurfaceArea = Abs(px2 * py1 - px1 * py2) * 0.5
End Function

(3点A,B,Cに囲まれる三角形の面積)


　どれか1点を、基準点である原点に「平行移動」し、 それにあわせて、他の2点も平行移動します。
A(x1,y1),B(x2,y2),C(x3,y3) の3点について考え、 点Cを原点に平行移動すると、
A'(x1-x3,y1-y3),B'(x2-x3,y2-y3),C'(0,0)
と表せます。 この新しい座標に対して、上の式を用いて面積を求めれば、 3点A,B,Cに囲まれる三角形の面積を求めたのと同じ事になります。

(多角形の面積)

『多角形は、三角形の集まりである』

と考えると、簡単に求めることができます。下の左図のように描かれた 多角形の面積を求める場合、原点Oを中心として、右図のように分割して それぞれの三角形の面積を求め、 その総和を得ることによって多角形の面積を求めることができます。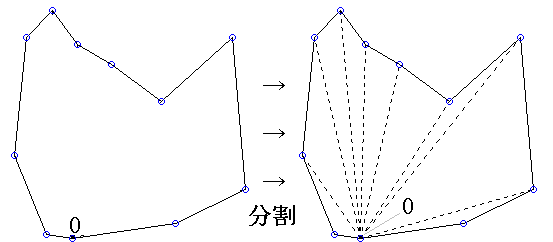

(注意点)

下のコードで面積を求める場合、当然の事ながら 各頂点が格納された配列は、要素番号0から左回りもしくは右回りの順序通りに 並んでいる必要があります。
多角形(閉路)の作成〜散在した点のソート〜 を用いてソートすれば、バラバラに格納された場合でも多角形の面積を求め ることができます。ただし、凹凸ができるように点が散在していたならば、 求められる面積が必ずしも意図したものではないということに注意して下さい。
（→複数の点を線分で結ぶことによる図形の相違） 

'閉路のための構造体
Private Type POSITION
    x As Double 'x座標
    y As Double 'y座標
    r As Double '基準点の水平位置からの角度(0〜2)
End Type

'座標(px1,py1)と(px2,py2)を結ぶ線分と原点によって囲まれる
'三角形の面積を求める
Public Function GetTriSurfaceArea(ByVal px1 As Double, _
                                  ByVal py1 As Double, _
                                  ByVal px2 As Double, _
                                  ByVal py2 As Double) As Double
    GetTriSurfaceArea = Abs(px2 * py1 - px1 * py2) * 0.5
End Function

'閉路によってソートされた配列で示される多角形の面積を求める
'PosData()   座標位置
'pdCount     頂点の数(n角形)
Public Function GetPolySurfaceArea(PosData() As POSITION, _
                                   pdCount As Long) As Double
    Dim i As Long                  'カウンタ
    Dim retS As Double             '求める面積
    Dim x1 As Double, y1 As Double '平行移動した後の座標
    Dim x2 As Double, y2 As Double
    
    '基準点の次の点の平行移動
    x1 = PosData(1).x - PosData(0).x
    y1 = PosData(1).y - PosData(0).y
    
    retS = 0#
    
    'n角形の場合、(n-2)個の三角形の面積を求める必要がある
    For i = 2& To pdCount - 1&
        x2 = PosData(i).x - PosData(0).x
        y2 = PosData(i).y - PosData(0).y
        retS = retS + GetTriSurfaceArea(x1, y1, x2, y2)
        '1つずつ点をずらす
        x1 = x2
        y1 = y2
    Next i
    
    GetPolySurfaceArea = retS
End Function

（参考書）

『アルゴリズムとデータ構造』
江村潤朗、上坂吉則、浅井宗海、有澤誠、西村俊介
実教出版

サンプルプログラムは、多角形(閉路)の作成〜散在した点のソート〜 との関連性から、そちらのみリンクしました。

Algorithmインデックス トップ

Copyright(C)2000 Tomoya. All rights reserved.