[Chapter5 制作物]
今回は、敵1の動作ルーチンを製作します。
■sca_enemy1.asm を追加
これまでにいくつかソースを追加してきましたが、同様の手順で sca_enemy1.asm を追加します。
追加のために修正するファイルは、mk.bat, chapter5.link になります。
修正の仕方は、これまでの chapter を参考に考えてみてください。
■敵1の動き
敵の動作はいろいろ作るのですが、そのうちの一つとして図1のような動きをする敵を、敵1と定義する
ことにします。
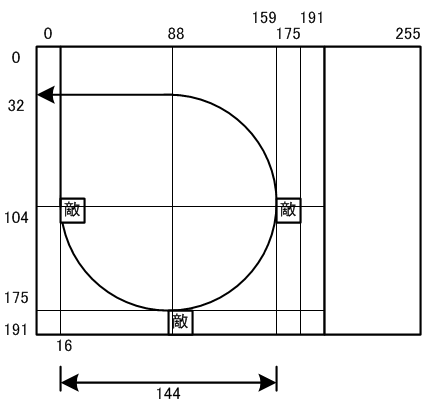
図1 敵1の動作
敵1出現時に、自機が中央より右側にいるときには図1と全く同じ動作。
敵1出現時に、自機が中央より左側にいるときには図1の動きを左右反転した動作にします。
もっと単純な動きの敵も作りますが、最初に難しい動きを実現しておけば、後は説明しなくても分かるはず
という都合で、いきなりこんな動きから作ることにしました・・・このテキストを端折るための策です (^_^;
実際に自分でゲームを作る場合は、簡単なモノから作ればいいと思います。
ただし、作り始める前にどんな動きをさせるつもりなのか、しっかり決めてから作り始めるようにしてください。
しっかり決まっていないモノを、作りながら組んでいくと、混乱して収拾が付かなくなり、挫折してしまうケース
が多いです。
図1を見てください。
まず、出現位置は、座標 (0,0) よりやや右側の上端です。
そこから、真下へ直進する動きを、"動き(1)"と名付けます。
次に、カーブでしばらく動き、(88,32)あたりまで 270度回転します。このカーブの動きを "動き(2)"と名付けます。
次に、左へ直進する動きを、"動き(3)" と名付けます。
一見複雑な関数に見える人もいるかも知れませんが、上記のように分けてしまえば分かりやすくなります。
図2に色分けしてみました。

図2 敵1の動作を動きの種類で分類
動き(1) → Y に定数を加算する動き
動き(2) → (n*cosθ+x, n*sinθ+y) でθを 270度回す動き
動き(3) → X に定数を減算する動き
この中で厄介なのが、sinθ とか cosθです。
MSX-BASIC の中で使われている sinθ, cosθ のサブルーチンはあります(*)が、浮動小数点を使っているために遅かったりして
使い勝手が悪いです。
( (*)MathPack というサブルーチン群で、MSX-BASIC の算術関数が集まっているサブルーチン群。通常の BIOS とはちょっと違う。)
そこで、sinθ,cosθ を求めるサブルーチンを自作することにします。
ついでに、Z80 にはかけ算命令も存在しないので、いきなり n*sinθ, n*cosθ の形で得られるルーチンを作ることにします。
θも、度単位では mod 360 などを実施したくなります。mod は剰余なので、割り算が必要になります。
割り算は、乗算よりも厄介な代物なので、これも可能ならば演算しないで済むようにしたいです。
なので、θは独自単位系を作り出して 512 で1回転を示す単位にしてしまいます。
こうすると、mod 512 を実施したくなりますが、これは and 511 と等価です。and 演算なら、高速に処理できますから、
この方が Z80 には都合が良いのです。
このような工夫だけで、演算速度が遅くなるのを防げるわけです。
■sin, cosを求める方法
Z80 で、実用な速度で計算するのは困難なので、あらかじめ求めておいてテーブル化してしまいます。
cos の1つの値を 1byte で表現するとして、512 通りの角度があるとすると、512byte。
sin も用意すると、倍になって 1024byte = 1KB になってしまいます。
たかだか 16KB 程度のゲームを作ろうとしているのに、sin/cos だけで 1KB も消費してしまうのは論外です。
なので、少しだけ Z80 に頑張って貰って、この容量を減らす工夫をします。
まず図3を見てください。

図3 sinθとcosθの関係
sinθとcosθは、sin(90度 - θ) = cosθ という関係がありますが、
これを利用することにより、cos か sin のどちらか一方だけ用意することで、
そこから引き算1つ追加するだけでもう一方を求めることができます。
これで 512byte
まだ多いです。
次に図4を見てください。
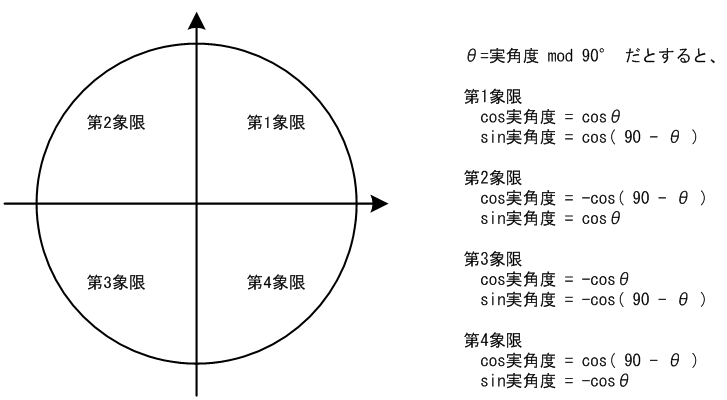
図4 sinθ, cosθの象限間の関係
仮にθを 0度〜90度の範囲に制限したとしても、第2〜4象限(90度〜360度)の sin/cos の値は求められます。
これを利用すれば、更に 1/4 に減らせます。
これで 128byte です。
128byte くらいなら、受け入れられる容量ですよね。
ということで、cos0度〜cos90度の範囲をテーブルで持つことにしました。
角度は、度ではなく独自の単位系で表現することにしたので、90度相当の場合 128段階の角度分解能があります。
なので、値も 128個の値になります。2のN乗にすることで、演算を簡素に出来るのです。どのように簡単になるかは後述します。
Excel 等を用いて、サクッと求めてしまいましょう。
cos.xls がそれです。
まず、独自単位の角度として 0〜127 を並べます(B列)。
次に、算術関数に渡せるようにラジアン単位に変換します。変換式は、(B列)*PI()/128/2 です。
90度が PI()/2 ラジアンで、そいつを 128等分したのが独自単位1つ分のラジアン値と言う意味です(C列)。
cos(C列) したのが D列です。
今回は、敵1の動き(2)におけるカーブの半径 72 にあわせて、72*cosθを実現したいので、D列の値に 72を掛けて
小数部を切り捨てたのが E列です。
この E列をテキストエディタに貼り付けて、.db なデータ羅列になるように加工していきます。

図5 Excelを用いたcosテーブル作成イメージ
プログラム1. 作った cosθテーブル
enemy1_cos_table: .db #72, #72, #72, #72, #72, #72, #72, #72 .db #72, #72, #72, #72, #72, #72, #71, #71 .db #71, #71, #71, #71, #70, #70, #70, #70 .db #69, #69, #69, #69, #68, #68, #68, #67 .db #67, #67, #66, #66, #66, #65, #65, #64 .db #64, #64, #63, #63, #62, #62, #61, #61 .db #60, #60, #59, #59, #58, #58, #57, #57 .db #56, #56, #55, #54, #54, #53, #53, #52 .db #51, #51, #50, #50, #49, #48, #48, #47 .db #46, #45, #45, #44, #43, #43, #42, #41 .db #41, #40, #39, #38, #38, #37, #36, #35 .db #34, #34, #33, #32, #31, #30, #30, #29 .db #28, #27, #26, #26, #25, #24, #23, #22 .db #21, #21, #20, #19, #18, #17, #16, #15 .db #15, #14, #13, #12, #11, #10, #9 , #8 .db #8 , #7 , #6 , #5 , #4 , #3 , #2 , #1 |
では早速、このテーブルを用いて sinθ, cosθを求めるプログラムを作っていきます。
HLレジスタに角度θを入力してcallすると、Cレジスタに cosθ, Bレジスタに sinθ を返すサブルーチンとします。
; input: ; hl ... θ (0 = 0[rad], 512 = 2π[rad]) ; output ; c ... cosθ ; b ... sinθ |
入力HLの角度イメージを図6に示します。
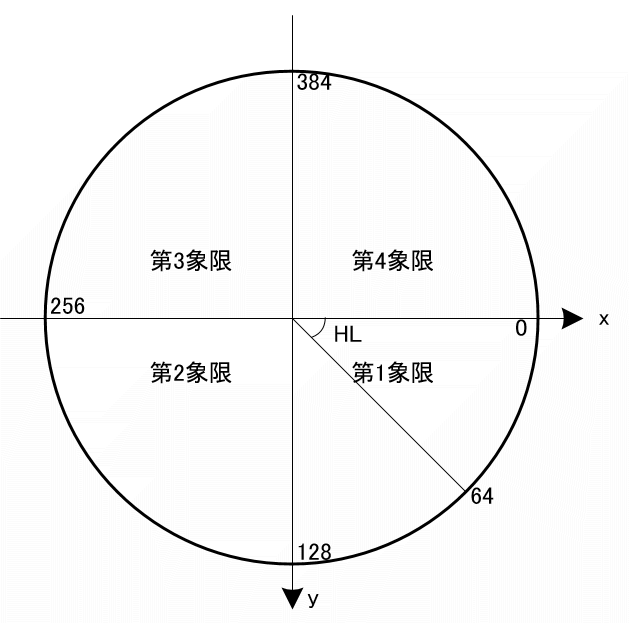
図6 入力値HLの角度のイメージ
画面の座標系のY軸は下が+なので、まずそれに合わせています。
右方向を角度0としたときに、角度が増加すると反時計回りに回る方向に進むルールとします。
角度θ[rad] に対して、HL に設定する値は下記のようになります。
HL = {θ[rad]} * 512 / 2π
ゲーム中にわざわざこの変換をするのは効率が悪いので、ゲームの中の角度表現はすべてこの単位で行うことにします。
そうすれば、単位変換演算は必要なくなります。
【note】
このあたりのルールは、自分で決められる部分なので、プログラムしやすいような都合の良いルールにします。
なかなかそのあたりの勘所が難しいうちは、まず数学でよく使われるものでも良いので仮のルールを設定して
プログラムを考えてゆき、「何らかの変換演算(単位変換とか方向の変換とか)」が伴った場合に、
「その変換が必要の無い座標空間とはどんなものか?」というのを一度考えてみると答えが見えやすいかもしれません。
そういった積み重ねをしていくうちに慣れてきて、最初からある程度「プログラムしやすい都合の良いルール」を考えやすくなります。
hl が 0〜127 は第1象限、128〜255 は第2象限, 256〜383 は第3象限, 384〜511 は第4象限に位置します。
cosθテーブルには第1象限の分しかありませんので、まずはこの4種を識別する値を抽出します。
hl の下位7bit (0〜127) が象限内での角度情報、上位2bit が象限の番号 - 1 であることが分かります。
つまり下記の式が成り立ちます。
HL = {角度情報} + ( {象限番号 - 1} << 7 )
<< 7 は 7bit左シフトという意味です。
{象限番号 - 1} は、H のbit0, L のbit7 に相当します。
【①角度HLの上位2ビットと象限の対応関係】
第1象限: H(bit0) = 0, L(bit7) = 0
第2象限: H(bit0) = 0, L(bit7) = 1
第3象限: H(bit0) = 1, L(bit7) = 0
第4象限: H(bit0) = 1, L(bit7) = 1
各象限ごとに、用意した cosθテーブルをどのように加工するのかをまとめます。
【②cosθを求めるためのcosθテーブルの加工】
第1象限: そのまま
第2象限: 256-HLをθとして利用して、得られた結果を符号反転
第3象限: HL-256をθとして利用して、得られた結果を符号反転
第4象限: 512-HLをθとして利用
これを少し細工して、数式のバリエーションを減らしてみます。
【③cosθを求めるためのcosθテーブルの加工2】
第1象限: HL and 127 をθとして利用
第2象限: 128 - (HL and 127) をθとして利用して、得られた結果を符号反転
第3象限: HL and 127 をθとして利用して、得られた結果を符号反転
第4象限: 128 - (HL and 127) をθとして利用
ここで上記①と③を見比べてみると、下記の関係があることが分かります。
工事中
[▲トップページへ]