|
*** (今回のサンプルもあくまで理論の追求を目的としました。ので、実際にこういう方法が 用いられることはあまりないと思います。(^^)) あかん、まだ勉強不足だ・・・。 ***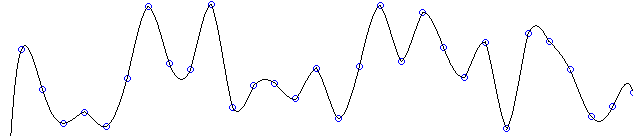 
5次の補間多項式を用いて描いた曲線株価の平滑線みたいな・・・ 「2点ずつ補間し、(点の数 - 1)個の多項式によって、曲線を描く」 という方法を用います。 これはスプライン補間的な考え方ですが、冒頭で触れたように、下のような 方法が一般的なものではないと思います。(^^) 「曲線は、(点の数 - 1)次の多項式で表すことができる」 という理論から、1次式になります。 しかし、描かれる曲線は直線ではなく、滑らかな線である必要があります。 描かれる曲線は、なめらかで急に折れ曲がったりしないものであることが 条件なので、高次の式で表さなくてはいけません。 しかし、2点間だと式は2つしかできないので、それを行うには 不可能に見えます。 そこで、前後の点を考慮に入れて補間します。4点を利用すれば、 3次の多項式、6点であれば5次の多項式を求めることができます。 式を求める段階にのみそれらの点を用い、実際に補間あるいは曲線を 描くとき、その2点間にのみ適用すればいいわけです。 当然、高次の多項式であればあるほど、より滑らかで自然な曲線が 描けますが、オーバーフローにも注意する必要があります。 コードは入りくんでややこしく見えますが、ロジックそのものは単純です。 |
Public Type POINT
x As Double
y As Double
End Type
Private Const N = 5&
'GaussJordan ガウス−ジョルダン法で連立方程式を解く
'詳しくはそのサンプルをご覧下さい
Private Function GaussJordan(value() As Double, _
count As Long) As Boolean
Dim a As Double
Dim i As Long, j As Long
Dim k As Long
Dim temp As Double
For i = 0& To count - 1&
a = value(i, i)
If Abs(a) < 1E-20 Then GaussJordan = False: Exit Function
For k = i To count
value(k, i) = value(k, i) / a
Next k
For j = 0& To count - 1&
If j <> i Then
temp = value(i, j)
For k = i To count
value(k, j) = value(k, j) - _
temp * value(k, i)
Next k
End If
Next j
Next i
GaussJordan = True
End Function
'与えられた点をすべて通る曲線を N 次数のスプライン的に描く
'N は奇数である必要あり、N = 3,5,7 ぐらいが適当です。
'Nが大きいほどより滑らかに描けます。
'果たしてこういう物がスプラインと言うのだろうか・・・
'pos() 点
'pCount 点の数
'sPic 描画先ピクチャボックス
'sx,ex 描画開始，終了位置
Public Function DrawCarveLine2(pos() As POINT, _
ByVal pCount As Long, _
ByVal sPic As Object, _
ByVal sx As Long, _
ByVal ex As Long)
Dim gj() As Double '連立方程式を解くための行列の値
Dim i As Long, j As Long, k As Long 'カウンタ
Dim y As Double '補間された値
Dim tempx As Long, tempy As Long '直線の始点保管
Dim hsx As Long, hex As Long '曲線を描く区間の始点と終点
ReDim gj(N + 1 - 1 + 1, N + 1 - 1) '[点の数]の正方行列
'座標スケールの定義
sPic.Scale (0, sPic.Height)-(sPic.Width, 0)
For k = N \ 2& To pCount - N \ 2& - 1& - 1&
'点のx,y値を連立方程式を解くための行列値にする
For j = 0& To N + 1& - 1&
For i = 0& To N + 1& - 1&
gj(i, j) = pos(j - N \ 2& + k).x ^ (N + 1& - 1& - i)
Next i
gj(N + 1, j) = pos(j - N \ 2& + k).y
Next j
'連立方程式を解く
If GaussJordan(gj, N + 1) = False Then Exit Function
tempx = 0&: tempy = 0&
hsx = pos(k).x
hex = pos(k + 1).x
If k = N \ 2& Then hsx = sx
If k = pCount - N \ 2& - 1& - 1& Then hex = ex
'連立方程式の解を使用して補間値を求め曲線を描く
For j = hsx To hex
y = 0#
For i = 0& To N + 1& - 1&
y = y + CDbl(j ^ (N + 1& - 1& - i)) * gj(N + 1, i)
Next i
If j <> hsx Then sPic.Line (tempx, tempy)-(j, CLng(y))
tempx = j: tempy = y
Next j
Next k
End Function
|
Private Const POS_C = 30&
Private Sub Command1_Click()
Dim p(POS_C - 1) As POINT
Dim i As Long
Picture1.Cls
Picture1.Scale (0, Picture1.Height)-(Picture1.Width, 0)
For i = 0 To POS_C - 1
p(i).x = CDbl((i + 1) * Picture1.Width / POS_C)
p(i).y = Int(Picture1.Height * Rnd)
Picture1.Circle (p(i).x, p(i).y), 3, RGB(0, 0, 255)
Next i
Call DrawCarveLine2(p, POS_C, Picture1, 0, Picture1.Width)
End Sub
|
| (参考) 上記以外のスプライン補間の考え方として、 2点間を3次の式で表し、点上の傾きを考慮して、 (点に入ってくる曲線と出ていく曲線の点上における傾きが等しい) 4つの式を作り、補間を行う方法があります。 |
| 機種 | PC-9821V13S |
| OS | Windows95 |
| 開発ツール | Visual Basic Ver.4.0 |
| 更新日 | 01/1/15 |
Visual Basic Ver.5.0,Ver.6.0でも問題なく動作すると思います。
なお、このコーナーに掲載されているプログラムコード、およびプログラムファ イルが原因で生じた損害などに関して一切の責任を負うことはできません。
★掲載されているプログラムコード、およびプログラムファイル、 ソースファイルを無断で配布・転載することは、原則として禁止です。