 |
|
この問題はしばしば相談を受けるのですが、
数学的理由と、数学の外の事情で難しいのです。
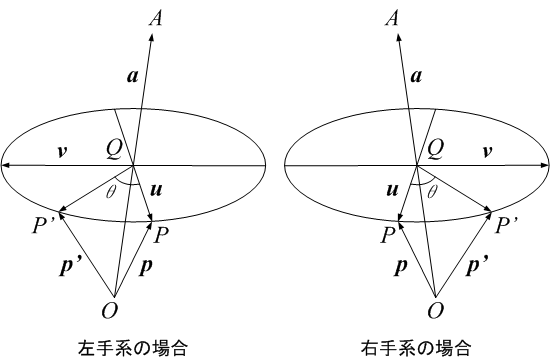
3次元空間内において,原点を通る任意方向の回転軸のまわりに 点を角度θだけ回転させたときの位置を求めよ.
 |
|
O→Q は単位ベクトル a に対する p の平行成分,u は垂直成分なので,
……………………………………… (2.2.1)
………………… (2.2.2)
v は定義より,
…………………(2.2.3)
a⊥u かつ |a|=1 なので,|u|=|v| である点に注意.
以上と u⊥v であることを考慮すると,回転後の位置 p' は2次元の回転の式を使って次のように書けることは明らか.
…………………(2.2.4)
ねっ,簡単でしょ?
なお,以上の計算式は座標系の取り方には依存しないので,
直交座標 (デカルト座標)でなくても
(斜交座標や極座標 (円柱座標,球座標など) でも) 使用できる.
ただし図にも描いたとおり,座標系の掌性
(chirality,
キラリティ,
カイラリティ:右手系と左手系の区別)
により回転方向の定義が逆になる点に注意.
(そうなる理由は,右手系と左手系では外積の向き (図の v の向き) の定義が逆になるから.)
今までの計算式は座標系の取り方に依存しなかったが,ここから先は正規直交座標系限定.
(よく知られている外積の成分の計算式が正規直交座標系を前提としているため.)
ベクトルは縦ベクトル,t を転置とする.例えば,
また行列 [a×] を,任意のベクトル a,p
について次式が成り立つように定義する.
("[a×]" はここで勝手に定義する記号なので,よそを探してもないよ.)
(2008/08/17(日) 追記:外積行列
(cross-product matrix)
というらしい.)
…………………(2.3.1)
つまり,
…………………(2.3.2)
これを用いると,(2.2.4) は次のように書ける.
…………………(2.3.3)
(I3 は3次の単位行列)
したがって回転行列 R(a, θ) は次のようになる.
…………………(2.3.4)
成分で書けば次のとおり.
…………………(2.3.5)
(δij は クロネッカーのデルタ,εikj は エディントンのイプシロン.)
(余談:英語版 Wikipedia には,εijk
を3次元行列 (3次行列ではない)
で表現した図がある.
また,εijk と δij の面白い関係式も載っている.)
なお,この行列を同次座標用に拡張したものは, OpenGL の glRotate (glRotatef, glRotatex) 関数でも用いられている. また DirectX の XMMatrixRotationAxis / XMMatrixRotationNormal (DirectXMath / XNA Math) や D3DXMatrixRotationAxis (D3DX) もこの行列を返すはず.
OpenCV では cv::Rodrigues().(2015/12/26(土) 追記)
時々「4次元 回転(行列)」などで検索して来る人がいるけど, 4次元空間の幾何学について考えている人がそんなにいるとは思えない. 3DCG に使うつもりで検索しているんだとしたら,まず間違いなく3次元の同次座標 (4成分) を4次元と勘違いしてるんだろう.
本当の4次元の回転について知りたい人は↓こっち.
ロドリゲスの回転公式 (Rodrigues' Rotation Formula) というらしい.
エディントンのイプシロンを用いた式は, 3次元外積の成分を統一的に表現することができるので代数的に扱うには都合がよい. しかし数値計算 (CG を含む) では, 無駄に積和演算と多次元配列のアクセスを増やすので遅い. クロネッカーのデルタについても同様. sinθ [a×] と cosθ I3 の非零要素だけを個別に加算するようハードコードする方がよい.
注)有限回転の式を,ロドリグの公式と呼びましたが, この式を導いたのはロドリグではないという説が有力です. この式自体は,実はもっと昔から知られていたようなのですが, ベクトルという概念がまだ無かったので,違った説明のされかたをされていました. ベクトルという概念を前面に押し出して,この公式を初めて導いたのはギブスのようです. こういった事情により,ロドリグの公式という言い方を避けて, ベクトルの回転公式などと呼ぶ人もいるようですが, 未だに定着している名前はありません.
■関連
ハミルトン (Hamilton) が発見した四元数から, 熱力学で有名なギブス (Gibbs) と,電気回路理論や演算子法で有名なヘヴィサイド (Heaviside) がそれぞれ独立にベクトル解析という分野を開拓したエピソード. (ちなみにホイートストン・ブリッジ回路で有名な Sir Charles Wheatstone はヘヴィサイドの叔父.)

 実務に役立てる!! 強引に...
実務に役立てる!! 強引に...
|
Androidゲームプログラミング A to Z posted with amazlet at 12.05.20 Mario Zechner インプレスジャパン 売り上げランキング: 26792 |

 素晴らしい本です。ぜひ1冊持っていたい本です。
素晴らしい本です。ぜひ1冊持っていたい本です。 群論への橋渡しに。
群論への橋渡しに。 群論への橋渡しに。
群論への橋渡しに。 群論の入門、線形代数の応用の学習に最適
群論の入門、線形代数の応用の学習に最適
 クォータニオンの本?
クォータニオンの本? 7章だけ別次元
7章だけ別次元 非常に難解だと思います。
非常に難解だと思います。 本書だけでクォータニオンを理解するのは難しいと思う
本書だけでクォータニオンを理解するのは難しいと思う クォータニオンを用いた3次元回転入門の適書
クォータニオンを用いた3次元回転入門の適書
 実務に役立てる!! 強引に...
実務に役立てる!! 強引に...
|
微分幾何学と接続―技術者のための (One Pointテキストシリーズ 11) posted with amazlet at 10.11.29 棚橋 隆彦 三恵社 売り上げランキング: 545133 |
|
|
理論的な説明 + サンプルプログラム.

 いまどき
いまどき 今から勉強するなら…買いである
今から勉強するなら…買いである WEB版とほぼ同じ
WEB版とほぼ同じ 入門書としてオススメ♪
入門書としてオススメ♪
 最初の1冊に最適
最初の1冊に最適 数値シミュレーション入門に。
数値シミュレーション入門に。 3次元CGの教科書向け
3次元CGの教科書向け あくまで入門書
あくまで入門書 入門用に
入門用に
 待望のバイブルついに OpenGL 2.0対応で帰ってきました
待望のバイブルついに OpenGL 2.0対応で帰ってきました お勧めです!
お勧めです!
 OpenGL ES に一歩近づけてくれる一冊です
OpenGL ES に一歩近づけてくれる一冊です iPhoneのOpen GLの最初の足がかりに
iPhoneのOpen GLの最初の足がかりに ヒントが沢山の良書です
ヒントが沢山の良書です
|
|

 お勧めです
お勧めです
 わかりやすいです
わかりやすいです 初心者には良い内容です
初心者には良い内容です 分かりやすい
分かりやすい とても良い入門書
とても良い入門書 非常にわかりやすい
非常にわかりやすい
 DirectX9 December 2004版
DirectX9 December 2004版 初心者向け
初心者向け
 わかっている人向けのリファレンス本
わかっている人向けのリファレンス本 新500の極意
新500の極意
 様々な技法が載ってます
様々な技法が載ってます Graphics Gemsの後継書
Graphics Gemsの後継書 やや敷居は高いかも
やや敷居は高いかも 日本のゲームプログラマーを目指す人に一冊
日本のゲームプログラマーを目指す人に一冊
 Game開発の辞書的な存在です
Game開発の辞書的な存在です
 実用的な手法を、演算レベルから解説した良書
実用的な手法を、演算レベルから解説した良書
 内容はいいのだが
内容はいいのだが 類書との違いは具体的なコードが載っていること
類書との違いは具体的なコードが載っていること タイトルに偽りなし
タイトルに偽りなし
 数学が嫌いなのにプログラマになった?
数学が嫌いなのにプログラマになった? 高校で習う内容
高校で習う内容 C言語と
C言語と 導入書なので仕方ないとは思いますが・・・
導入書なので仕方ないとは思いますが・・・ 3Dのゲームと数学
3Dのゲームと数学
 多くの情報への窓口となる本
多くの情報への窓口となる本 実践的な衝突判定技術を広範囲にカバー
実践的な衝突判定技術を広範囲にカバー 衝突最高!
衝突最高!
|
内積・外積・空間図形を通して ベクトルを深く理解しよう (数学のかんどころ 1) posted with amazlet at 11.11.03 飯高 茂 共立出版 売り上げランキング: 190055 |
|
|
|
なっとくする行列・ベクトル (なっとくシリーズ) posted with amazlet at 11.11.03 川久保 勝夫 講談社 売り上げランキング: 172378 |
|
ベクトル・行列がビジュアルにわかる線形代数と幾何 posted with amazlet at 11.11.03 江見 圭司 江見 善一 共立出版 売り上げランキング: 158714 |
|
|
|
細野真宏のベクトル〈平面図形〉が本当によくわかる本―数B (1週間集中講義シリーズ) posted with amazlet at 11.11.03 細野 真宏 小学館 売り上げランキング: 32875 |
|
細野真宏の ベクトル〈空間図形〉が本当によくわかる本 1週間集中講義シリーズ posted with amazlet at 11.11.03 細野 真宏 小学館 売り上げランキング: 8392 |
|
|
|
坂田アキラの三角関数・指数・対数が面白いほどわかる本 新装版―数学2対応 (数学が面白いほどわかるシリーズ) posted with amazlet at 11.11.03 坂田 アキラ 中経出版 売り上げランキング: 17311 |
|
山本俊郎のベクトル原則編が面白いほどわかる本 (数学が面白いほどわかるシリーズ) posted with amazlet at 11.11.03 山本 俊郎 中経出版 売り上げランキング: 142524 |
|
山本俊郎のベクトル実戦編が面白いほどわかる本 (数学が面白いほどわかるシリーズ) posted with amazlet at 11.11.03 山本 俊郎 中経出版 売り上げランキング: 331107 |
|
イラスト・図解 はじめての行列とベクトル posted with amazlet at 11.11.03 長谷川 勝也 技術評論社 売り上げランキング: 220444 |
|
なるほど高校数学 ベクトルの物語 (ブルーバックス) posted with amazlet at 11.11.03 原岡 喜重 講談社 売り上げランキング: 229182 |
|
なるほど高校数学 三角関数の物語 (ブルーバックス) posted with amazlet at 11.11.03 原岡 喜重 講談社 売り上げランキング: 158574 |
|
|
この問題はしばしば相談を受けるのですが、
数学的理由と、数学の外の事情で難しいのです。
「オイラー角」や「ロール ピッチ ヨー (カルダン角)」等で検索して来た人は必読!
GameDev?.orgで2003年2月に投稿された“Quaternion Powers”(Sobeit Void氏著)の無許可な和訳です。元記事:http://www.gamedev.net/reference/articles/article1095.asp
注意
以前機械系の方と、3 次元の合同アフィン変換 (回転 + 平行移動からなる合同変換) の、回転と平行移動を求める方法に関して話を聞いたことがあり、 その方法が多少面白い方法であったので、ここにまとめておく。
このページの主な更新は Blog でお知らせします.
|
Copyright © 2008-2015 noocyte. E-mail: relipmoced (a) yahoo.co.jp (" (a) " を半角のアットマークに書き替えてください.) リンクはご自由に. 「幾何学・CG のアルゴリズム集」に戻る. 「noocyte のプログラミング研究室」トップページに戻る. |