noocyte
�̃v���O���~���O������ �`�v���O�����͊y�����ɑ���˂Ȃ�Ȃ���`
�R�_�̍��W����ȒP�Ɋp�x�Ɖ�]���������߂�D
(2�E3�EN�����C�O�ς�p������@)
���J�F2006/10/11(��)
�ŏI�X�V�F2016/04/03(��)
���}�ɂ����āC���� CP ���_ C �𒆐S�Ɋp�x�� (-180���� �� �� +180��)
������]�������ʁC
���� CQ �ɂȂ����Ƃ���D�R�̓_�̍��W
C��(Cx, Cy), P��(Px, Py), Q��(Qx, Qy)
���^����ꂽ�Ƃ��C���̉�]���E��肩����肩�ʂ���D
(�ʂ̌�����������C�uC �� P �� Q �� C �͉E��肩����肩�H�v)
�x
��
�� �p
�� �^
�� �^��
�� �b���������o
��
�n�������������������w
S �� (Px - Cx) * (Qy - Cy) - (Py - Cy) * (Qx - Cx)
�Ƃ���DS��0 �Ȃ獶���CS��0 �Ȃ�E���CS��0 �Ȃ�� C�CP�CQ
�͈꒼����ɂ���D(��)
�Ȃ��C���̔��ʕ��@�́CCP �� CQ �����������ł���K�v�͂Ȃ��D
�Ƃ����߂����ꍇ���������ցD
���̖������āC�t�O�p�� tan-1 (�b����ł� atan() �� atan2())
���g���� CP �� CQ �̊p�x�����ꂼ�ꋁ�߁C
���҂��r���悤�ƍl�������������̂ł͂Ȃ��ł��傤���D
���������̖��ł́C�p�x���̂��̂ł͂Ȃ��p�x���̕��������߂�悢�̂ŁC
�t�O�p�����g�����@�����ȒP�ŗD�ꂽ�C�O�ς��g�����@���Љ�܂��D
�Q�̂Q�����x�N�g�� A��(Ax, Ay), B��(Bx, By)
���O�������̂悤�ɒ�`����D
A �~ B �� Ax * By �| Ay * Bx
������ OA ���� OB �ւ̉�]�p���� (-180���� �� �� +180��) �Ƃ��� (���})�D
������ OA ���� OB �ɉ�]��������������Ȃ�� �Ɓ��O �Ƃ���D
���̂Ƃ��CA�~B �� |OA| * |OB| * sin�� �ł���D���������āC
- A �~ B �̕����̓Ƃ̕����Ɠ����D���Ȃ�����C���Ȃ�ΉE���D
- |A �~ B| �́COA �� OB ���Q�ӂƂ��镽�s�l�ӌ`�̖ʐρD(�� ��OAB �̖ʐς̂Q�{)
�x
��
�� �a
�� / �� �`
�� / �^
�� / �^
��/�^
�n�����������������w
���̂悤�ɊO�ς��g���C�Q��̏�Z�����ł��ނ̂ŁC(�x��)
�t�O�p���T�u���[�`�����g�����@�ɔ�ׂĎ��̂悤�ɂ������Ƃ����߂ł��D
- �����D
- �v�Z�덷�����Ȃ��D
- ���W�������Ȃ�C�O�ς��������Z�ł��ށD���̏ꍇ�v�Z�덷�͂O�D(�������I�[�o�[�t���[�ɒ���)
- �t�O�p���ł͊p�x�ɕs�A���_������̂ŁC
�Q�̊p�x���r���悤�Ƃ���Əꍇ�������K�v�ŁC���������G�ɂȂ�D
�܂��C�p�x�̂킸���Ȍv�Z�덷���ꍇ�����┻�茋�ʂɉe������ꍇ������D
�O�ς�p����ƉɎ������悤�ɏꍇ�����͕s�v�ŁC�P��̐������v�Z���邾���ł悢�D
�܂��C�Q�̃x�N�g���̉�]�p (��L�̃�) �����߂�ꍇ�ɂ́C
��q����悤�ɓ��ςƊO�ςp����ΊȒP�ł��D
���̏ꍇ���C�Q�̃x�N�g�����ꂼ��̊p�x�����߁C
�����̍����v�Z���悤�Ƃ���Əꍇ�������K�v�ɂȂ���ł��D
�Ȃ��C�O�ς͂R�����Ŏg���邱�Ƃ������C
�u�O�ρv�Ō������Ă��q�b�g����̂͑����قƂ�ǂ��R�����̘b���Ǝv���܂��D
�R�����x�N�g�����m�̊O�ς��R�����x�N�g���ɂȂ�܂����C
�Q�����x�N�g�����m�̊O�ς��X�J���[�ɂȂ�܂��D
(�R�����O�ςɂ����āC���̂Q�̃x�N�g�����w�x���ʓ��ɂ���ꍇ���l����C
�O�ς̂w�C�x�����͂O�ɂȂ�D���̂��߂y�����������l����悭�C
������Q�����̊O�ςƍl���邱�Ƃ��ł���D)
��̉���щ���ŁC�u�O�ς̒l�����Ȃ�����v�Ə����܂������C
����͂w������тx���̕�������̐}�̂悤�ɂȂ��Ă���ꍇ�ł��D
�����x���������� (���邢�͂w����������)
�ɂȂ��Ă���Ή�]�̌������t�ɂȂ�܂��D(���̒�)
�����ň�ʓI�Ȍ�����������ƁC���̂悤�ɂȂ�܂��D
OX ��90����]���� OY �ɂȂ�����𐳉�]�Ƃ���ƁC
�O�ς����Ȃ�ΐ���]�C���Ȃ�t��]�D
��������ǂ�ŁC
���̂悤�ȋ^��������ꂽ���������ł��傤�D
(a) �u�R�����x�N�g�����m�̊O�ς͂R�����x�N�g���Ȃ̂ɁC
�Ȃ��Q�����x�N�g�����m�̊O�ς͂Q�����x�N�g���ł͂Ȃ��X�J���[�Ȃ̂��H�v
���邢�́C�R�����O��������m���Ă���l�Ȃ�C���̂悤�Ɏv��ꂽ��������܂���D
(b) �u�����C�Q�����O�ς��X�J���[���Ăǂ��������ƁH
���������O�ς��ĂR�����ȊO�Œ�`�ł���́H�v
(a) �̂悤�ɂȂ闝�R�́C
�R�����̊O�ς̒�`������Ƃ킩��܂����C
�O�ς̂P�̐������v�Z����̂ɁC
���̂Q�̃x�N�g���̂Q�̍��W���̐������g���Ă��邱�Ƃɂ���܂��D
�Ⴆ�R�����O�ς̂w�������v�Z����ɂ́C
���̂Q�̃x�N�g���̂x����тy�������g���܂��D
�Q�̍��W���̑g�������ƂɁC�O�ς̓Ɨ��������P�Ή����܂��D
�O�ς̊e�Ɨ������́C�m������ԓ��̉�]���C
�Q�̍��W�������镽�ʂɓ��e�������̂ɑΉ����Ă���ƍl�����܂��D
���������Ăm�����x�N�g�����m�̊O�ςɂ́C
NC2 �̓Ɨ��Ȑ���������܂��D
�R�����ł͂��܂��� 3C2��3
�Ȃ̂Ńx�N�g���Ƃ��ĕ\���ł��܂����C
�Q�����ł͂��܂��� 2C2��1
�Ȃ̂ŃX�J���[�Ƃ��ĕ\���ł��܂��D
��ʂ̂m�����ł́C�x�N�g��
A��(A1, A2, �c, AN)
�� B��(B1, B2, �c, BN) ���O���́C���̂悤�� N�~N �s��ŕ\���ł��܂��D
((���`�̋L���Ȃ���) �E�F�b�W�ρC(�l�ĎҖ�����) �O���X�}���ςƂ������D)
| A �� B �� (Ai * Bj �| Aj * Bi) �� |
| 0 |
A1 * B2 - A2 * B1 |
�c |
A1 * BN - AN * B1 |
| A2 * B1 - A1 * B2 |
0 |
�c |
A2 * BN - AN * B2 |
| : |
: |
: |
: |
| AN * B1 - A1 * BN |
AN * B2 - A2 * BN |
�c |
0 |
|
���͂��ꂪ�{���̊O�ς̒�`�ł���C
�x�N�g���ł��X�J���[�ł�����܂���D
��̐����ł́u�s��ŕ\���v�Ə����܂������C
���m�Ɍ����ƊO�ς͂Q�K���e���\���ƌĂ��ʂł��D
�m�K�̃e���\���Ƃ́C��G�c�Ɍ����C�u�m�����̍s��v�̂悤�Ȃ��̂ƍl���Ă��������D
�O�K�̃e���\���̓X�J���[�C�P�K�̃e���\���̓x�N�g���ł��D
����ɐ��m�Ɍ����ƁC�O�ς͂Q�K��
���Ώ� �[�e���\���ł��D
�u���Ώ��v�Ƃ����̂́C��ɏ������s��̍s�Ɨ�����ւ����
(�܂�]�u�s��ɂ����)�C���������]����Ƃ������Ƃł��D
�u�[�v�Ƃ́C�u�E�ƍ������ւ��遁���W�n�̌����]������
(��{�̍��W�����t�����ɂ���C���邢�͂Q�{�̍��W������������) �ƁC
���������]����v���Ƃ��Ӗ����܂��D
�����̒�
��́u�����v�ŁC
���W�n�̌����ɂ���ĊO�ς̕����ɑΉ������]�̌������ς��Ƃ����Ӗ��̂��Ƃ������܂������C
����͂Q�����O�ς��[�X�J���[������ł��D
���l�ɂR�����O�ς��[�x�N�g�� (�����x�N�g���Ƃ�����) �ł��D
���NjL (2010/02/10(��))
�����x�N�g���Ɋւ���ڂ��������D
���Z���w�a�ł͂Q�`�R�����x�N�g�������K��Ȃ����C���������낤��
(�����������낤��)�C�x�N�g�� A��(Ax�CAy�CAz�C�c) �� B��(Bx�CBy�CBz�C�c)
�����ς̒�`�́C
�w�I��`�FA�EB �� |A| * |B| * cos��
�㐔�I��` �FA�EB �� Ax * Bx + Ay * By + Az * Bz + �c
���������� A �� B �̂Ȃ��p�Ƃ́C
A�EB
cos�� �� ��������
|A||B|
Ax * Bx + Ay * By + Az * Bz + �c
�� ��������������������������������������������������
��((Ax2 + Ay2 + Az2 + �c)(Bx2 + By2 + Bz2 + �c))
���Ƃ͋t�O�p�� cos-1 ���g�������Ń� (0���� �� �� 180��) �����܂�D
�Q�����̏ꍇ�� Az ����� Bz
�Ȍ���O�Ƃ���悢�D
���ς��g���ƁC�������̂Ȃ��p�ł����߂��邪�C��]�����̏��͓����Ȃ��D
- �uExcel ���ρv
- Excel �ɓ��ρu��p�v�̊��͂���܂���DSUMPRODUCT �����g���Ă��������D
���Q�l
- �u�Ȃ��p 180�x�ȏ�v�u�Ȃ��p �����v
- �Ȃ��p�͕��� 0߁��Ɓ�180� �ł��D�ǂ��������Ȃ̂��킩��Ȃ����ǁC
��]�p�ƊԈႦ�Ă܂��H ��]�p�Ȃ�� 180� �ȏ�Ƃ��ȉ��Ƃ������O�ɁC
�܂���]�������`���Ă��������D
���Q�l
- �u���� ��]�����v
- ���ς͉�]�����Ƃ͑S���W����܂���D
- �u�Ȃ��p �O�ρv
- �t�Ɂu�Ȃ��p �O�ρv�Ō������ė���l�����邯�ǁC�O�ς͂Ȃ��p�����߂�̂ɂ͌����Ă��܂���D
- �u�Ȃ��p�v�͕��� 0�����Ɓ�180���ŁC��]�����̈Ⴂ�͖������܂��D
�������O�ς� sin�� �ɔ�Ⴗ��̂ŁC(��]�����������)
0���`90���͈̔͂��������܂���D(���̐}������킩��Ƃ���)
�O�� (����) �ł� 0�`90���� 90�`180������ʂł��܂���D
(�Ⴆ��45����135���ł� sin�� �̒l�������ɂȂ�̂ŁC�����̊p�x����ʂł��Ȃ��D)
- �R�����ȏゾ�ƊO�ς̓X�J���[�ł͂Ȃ��x�N�g����e���\���ɂȂ�̂ŁC
�v�Z�����ɕ��G�ɂȂ�܂��D(�Ȃ��p��90���ȓ��̏ꍇ�ł����Ă�)
���ς��g�������͂邩�ɊȒP�D
![[�摜�Fsin�� cos�� tan��]](RotationDirection/SinCosTan-s.gif)
���X�C�u�Ȃ��p�v,�u�p�x�v,�u�t�O�p���v,�uatan2�v
�ȂǂŌ������Ă���l������̂ł��܂��D(2006/12/13(��))
�Q�����x�N�g�� A �� B �̓��ς���ъO�ς̒�`�����߂ď����ƁC
�w�I��`�FA �E B �� |A| * |B| * cos��
�@�@�@�@�@�@�@A �~ B �� |A| * |B| * sin��
�㐔�I��` �FA �E B �� Ax * Bx + Ay * By
A �~ B �� Ax * By - Ay * Bx
�Ȃ̂ŁC���҂p����ƊȒP�Ɋp�x����щ�]���� (-180���� �� �� +180��) �����܂�D
C/C++ �̏ꍇ�� atan2(y, x) ���CC# �̏ꍇ��
Math.Atan2(y, x) ���g���ƁC
�� �� atan2(A�~B�CA�EB) (�P�ʂ����W�A���C�����̏����ɂ�����)
Excel �� ATAN2(x, y) ���͂b�� atan2(y, x) �Ƃ͈����̏������t�Ȃ̂ŁC
�� �� ATAN2(A�EB�CA�~B)
![[�摜�Fsin�� cos�� tan��]](RotationDirection/Atan2CrossDot-s.gif)
���Q�l
�R�����x�N�g�� A �� B ���O�� (�x�N�g���ρC�N���X�ςƂ�����) A�~B �̒�`�́C
��w�P�N���x�����͊w�C�d���C�w�C�������w�̋��ȏ��Ƀf�J�f�J�Ə����Ă���͂�
(�������قƂ�ljE��n����)�D
�ŋ߂ł́C3DCG ��Q�[���v���O���~���O�̖{ (�̈ꕔ�H) �ł��������Ă���D
�u�O�� ���ߕ��v�ȂǂŌ������ė���l���������ǁC
���ȏ��ǂ��Ƃ��Ȃ������牽�Łu�O�ρv�Ƃ������t��m���Ă�́H (����)
�w�I��`�F|A �~ B| �� |A| * |B| * sin�� (0���� �� �� 180��)
��]�ɑ��� A �~ B �̌����́C���W�n���E��n�Ȃ�ΉE�l�W�̐i�ޕ����C
����n�Ȃ���l�W�̐i�ޕ����D(A�F�e�w�����CB�F�l�����w�����CA�~B�F���w����)
�㐔�I��` �FA �~ B �� (Ay * Bz - Az * By, Az * Bx - Ax * Bz, Ax * By - Ay * Bx)
�Ƃ����߂���@�Ƃ��āC�Q�����̏ꍇ�Ɠ��l�ɊO�ςƓ��ςp���邱�Ƃ��\�����C
�R�����ł͌v�Z�������G�ɂȂ邾���Ń����b�g�� (���Ԃ�) �Ȃ��̂ŁC
6.1 �̕��@���g�����������Ǝv���D
��]�����ɂ��ẮCA�~B ���̂����̕�����\���Ă���̂ł��̂܂g���Ă��悢���C
�P�ʃx�N�g���ɂ���K�v������ꍇ�ɂ͐��K������ A�~B / |A�~B| �Ƃ���悢�D
�����F�S�����ȏ�̉�]�ɂ��Ă����ƍl�����킯�ł͂Ȃ��̂ŁC
���̐߂ɏ����Ă��邱�Ƃ�ǂޑO�ɁC���ɑ����x�b�g���Ƃ��Ăق����D(��)
�܂���]�p (�Ȃ��p) �́C�������ł��낤��
6.1 �̕��@�ŋ��߂邱�Ƃ��ł���D(����͊ԈႢ�Ȃ��D)
�u�]�k (�m�����̊O�ςɂ���)�v
�ɏ��������ƂƂQ�`�R�����̉�]����ސ�����C
�m�����ł���������������͂��ł���D
|A �� B| �� |A| * |B| * sin�� (0���� �� �� 180��)
�������m�����O�σe���\�� A��B �́u�����v�͎��̂悤�ɒ�`����D
|A �� B| �� �� (�� (Ai * Bj - Aj * Bi)2)
i��j
�� �� ((1/2) ���� (Ai * Bj - Aj * Bi)2)
i j
�R�����Ɠ��l�CA��B ���̂����́u��]�����v��\���Ă��邪�C
����𐳋K������� A��B / |A��B| �ƂȂ�D
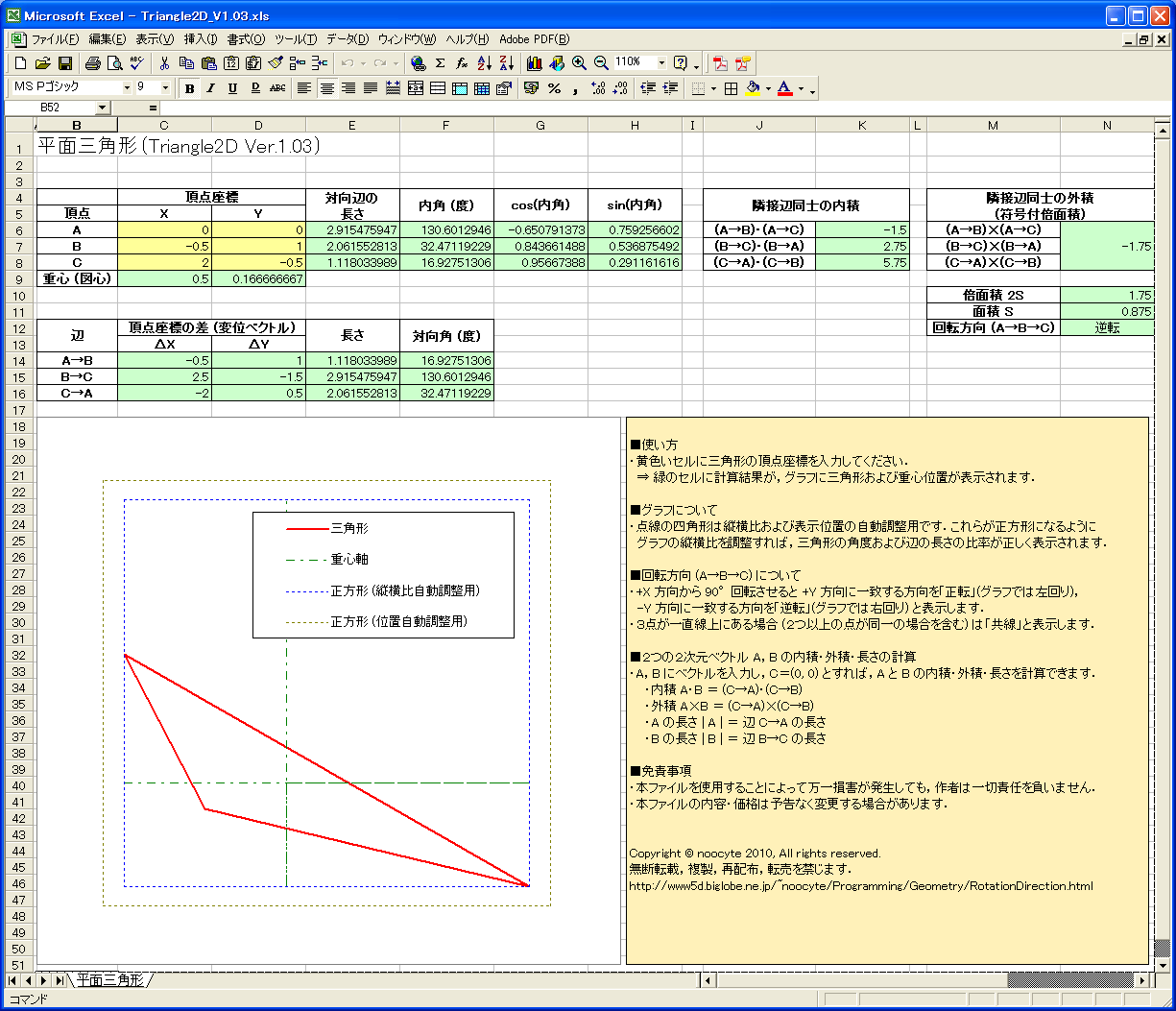
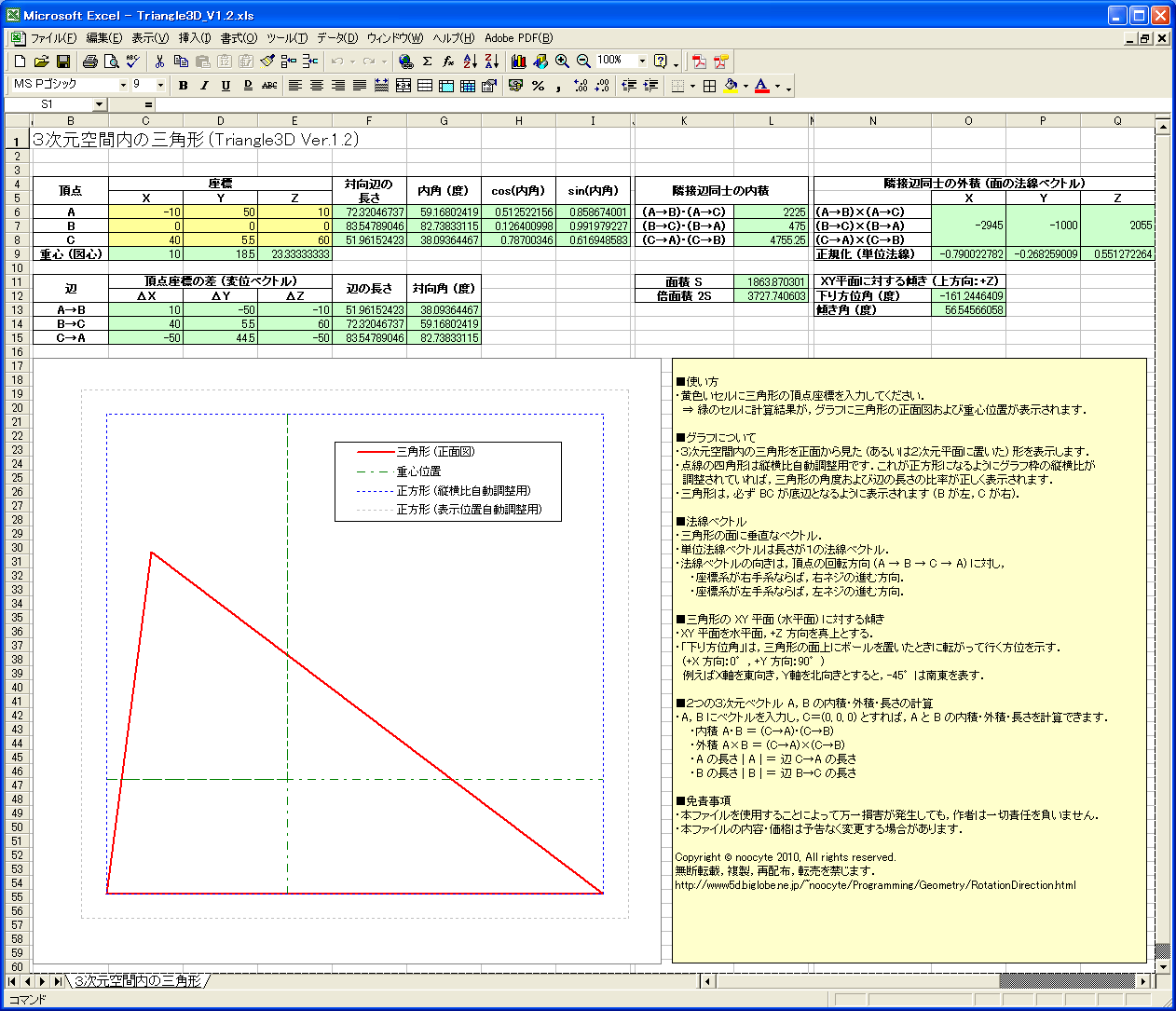
�R�_�̍��W (�Q�����܂��͂R����) ����͂��邾���ŁC�����I�Ɏ��̒l���v�Z����
Excel �t�@�C�����CDLmarket �l�ɂĈϑ��_�E�����[�h�̔����Ă��܂��D
- �O�p�`�̕ӂ̒����C���p�C�ʐρC�d�S (�}�S) �ʒu�D(�Q�����C�R����)
- �Q�̃x�N�g���̓��ρC�O�ρC�����C�Ȃ��p�C��]�����D(�Q�����C�R����)
- ������ (XY ����) �ɑ���O�p�` (���܂ޕ���) �̌X�� (�p�x�C����)�D(�R�����̂�)
- �O�p�`�̖@���x�N�g�� (�R�_���܂ޖʂɐ����ȃx�N�g��)�D(�R�����̂�)
/*��������������������������������������������������������������������������
�@�\ �F�Q�̃x�N�g���̊O�ϐ������v�Z����D
���� �F(1) vector1�Cvector2�F�x�N�g�� (�\���̂̃A�h���X�܂��͔z��)�D
(2) component1�Ccomponent2�F�x�N�g���̍��W�����D�x�N�g�����\���̂�
�ꍇ�̓����o���C�z��̏ꍇ�͐����ԍ� (�Y��)�D
�߂�l�F�O�� vector1��vector2 �� (component1�Ccomponent2) �����D
2009/03/13(��) �쐬
��������������������������������������������������������������������������*/
// �x�N�g�����\���̂̏ꍇ
#define CrossProductComponentS(vector1, vector2, component1, component2) \
((vector1)->component1 * (vector2)->component2 - \
(vector1)->component2 * (vector2)->component1)
// �x�N�g�����z��̏ꍇ
#define CrossProductComponentA(vector1, vector2, component1, component2) \
((vector1)[component1] * (vector2)[component2] - \
(vector1)[component2] * (vector2)[component1])
/*��������������������������������������������������������������������������
�@�\ �F�Q�̂������x�N�g���̃E�F�b�W�� (�O�σe���\��)���v�Z����D
���ʂȌv�Z������邽�߁C�Ɨ������̂��߂�D
���� �F(1) vector1[0 �` n-1]�Cvector2[0 �` n-1]�F�������x�N�g�� (�z��)�D
(2) n (��2)�F�x�N�g���̎����D
�o�� �FwedgeProduct[0 �` nC2-1]�F�E�F�b�W�� vector1��vector2 �̓Ɨ������̔z��D
���� �Fn��3 �̏ꍇ�CwedgeProduct[] �̗v�f�̏�������ѕ����́C�ʏ�̂R����
�O�ς̒�`�Ƃ͈قȂ�D������u�R�����O�ς̃v���O�������쐬����v��
�����w�Z�̉ۑ�ł�����ێʂ����Ă��_����D(��)
2009/03/13(��) �쐬
2013/01/14(��) ���� (VectorN_CrossProduct �� VectorN_WedgeProduct)
��������������������������������������������������������������������������*/
typedef double VectorComponent_t; // �x�N�g���̐����̌^
void VectorN_WedgeProduct(VectorComponent_t wedgeProduct[/* nC2 */],
const VectorComponent_t vector1[/* n */],
const VectorComponent_t vector2[/* n */],
unsigned n)
{
unsigned i, j;
for(i = 0; i < n; i++) {
for(j = i; ++j < n; ) {
*wedgeProduct++ = (VectorComponent_t)CrossProductComponentA(vector1, vector2, i, j);
}
}
}
#ifdef _MSC_VER
#define _USE_MATH_DEFINES // Visual C/C++ �ł́CM_PI ���g���̂ɂ��ꂪ�K�v�D
#endif /* _MSC_VER */
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
// ���W�A����x�ɕϊ�����D
#define RadianToDegree(radian) ((180 / M_PI) * (radian))
// �x�����W�A���ɕϊ�����D
#define DegreeToRadian(degree) ((M_PI / 180) * (degree))
// �x�N�g���̐����̌^
typedef double VectorComponent_t;
// �Q�����x�N�g��
typedef struct {
VectorComponent_t x, y;
} Vector2_t;
// diff �� �x�N�g�� v1 - v2
void Vector2_Diff(Vector2_t *diff, const Vector2_t *v1, const Vector2_t *v2)
{
diff->x = v1->x - v2->x;
diff->y = v1->y - v2->y;
}
// �x�N�g�� v1 �� v2 �̓��� (v1�Ev2) ��Ԃ��D
VectorComponent_t Vector2_DotProduct(const Vector2_t *v1, const Vector2_t *v2)
{
return v1->x * v2->x + v1->y * v2->y;
}
// �x�N�g�� v1 �� v2 �̊O�� (v1�~v2) ��Ԃ��D
VectorComponent_t Vector2_CrossProduct(const Vector2_t *v1, const Vector2_t *v2)
{
return v1->x * v2->y - v1->y * v2->x;
// return CrossProductComponentS(v1, v2, x, y); �ł��悢�D
}
// �x�N�g�� C��P �� C��Q �̂Ȃ��p�Ƃ���щ�]���������߂�D
int main(void)
{
Vector2_t c, p, q; // ���̓f�[�^
Vector2_t cp; // �x�N�g�� C��P
Vector2_t cq; // �x�N�g�� C��Q
VectorComponent_t s; // �O�ρF(C��P) �~ (C��Q)
VectorComponent_t t; // ���ρF(C��P) �E (C��Q)
double theta; // �� (���W�A��)
// c�Cp�Cq �����]�̒l�ɐݒ肷��D
c.x = 1;
c.y = 2;
p.x = 2;
p.y = 3;
q.x = 3;
q.y = 5;
// ��]��������ъp�x�Ƃ��v�Z����D
Vector2_Diff(&cp, &p, &c); // cp �� p - c
Vector2_Diff(&cq, &q, &c); // cq �� q - c
s = Vector2_CrossProduct(&cp, &cq); // s �� cp �~ cq
t = Vector2_DotProduct(&cp, &cq); // t �� cp �E cq
theta = atan2(s, t);
// ���ʂ��o�͂���D
printf("�b��(%G, %G)\n", c.x, c.y);
printf("�o��(%G, %G)\n", p.x, p.y);
printf("�p��(%G, %G)\n", q.x, q.y);
printf("�Ɓ�%G���W�A�� (%G�x)\n", theta, RadianToDegree(theta));
if(s == 0.0) {
printf("�R�_ �b�C�o�C�p �͈꒼����ɂ���B\n");
} else {
printf("�b���o���p��%s���B\n", (s > 0.0) ? "��" : "�E");
}
return EXIT_SUCCESS;
}
���s���ʁF
�b��(1, 2)
�o��(2, 3)
�p��(3, 5)
�Ɓ�0.197396���W�A�� (11.3099�x)
�b���o���p�͍����B
|
|
Mario Zechner
�C���v���X�W���p��
����グ�����L���O: 26792
|
|
|
�ז� �^�G
���w��
����グ�����L���O: 32875
|
|
|
�ז� �^�G
���w��
����グ�����L���O: 8392
|
|
|
�u�c ��
���o�o��
����グ�����L���O: 43835
|
|
|
��c �A�L��
���o�o��
����グ�����L���O: 17311
|
|
|
�R�{ �r�Y
���o�o��
����グ�����L���O: 142524
|
|
|
�R�{ �r�Y
���o�o��
����グ�����L���O: 331107
|
|
|
���J�� ����
�Z�p�]�_��
����グ�����L���O: 220444
|
|
|
���� ��d
�u�k��
����グ�����L���O: 229182
|
|
|
���� ��d
�u�k��
����グ�����L���O: 158574
|
|
|
���쎛 �ÍF
�u�k��
����グ�����L���O: 122943
|
|
|
��v�� ���v
�u�k��
����グ�����L���O: 172378
|
|
|
�э� ��
�����o��
����グ�����L���O: 190055
|
|
|
�]�� �\�i �]�� �P��
�����o��
����グ�����L���O: 158714
|
|
|
�呺 ��
���ȋZ�A�o�Ŏ�
����グ�����L���O: 248023
|
�� ���g
��g���X
����グ�����L���O: 279365
�������ߓx�̕���:


�f���炵���{�ł��B���ЂP�������Ă������{�ł��B

�Q�_�ւ̋��n���ɁB

�Q�_�ւ̋��n���ɁB

�Q�_�̓���A���`�㐔�̉��p�̊w�K�ɍœK
|
|
���}�� �S��
�X�k�o��
����グ�����L���O: 285345
|
���_�I�Ȑ��� �{ �T���v���v���O�����D
Wendy Stahler
�\�t�g�o���N�N���G�C�e�B�u
����グ�����L���O: 57346
�������ߓx�̕���:


���w�������Ȃ̂Ƀv���O���}�ɂȂ����H

���Z�ŏK�����e

C�����

�������Ȃ̂Ŏd���Ȃ��Ƃ͎v���܂����E�E�E

�RD�̃Q�[���Ɛ��w
Fletcher Dunn Ian Parberry
�I���C���[�W���p��
����グ�����L���O: 5010
�������ߓx�̕���:


���e�͂����̂���

�ޏ��Ƃ̈Ⴂ�͋�̓I�ȃR�[�h���ڂ��Ă��邱��

�^�C�g���ɋU��Ȃ�
Christer Ericson
�{�[���f�W�^��
����グ�����L���O: 64052
�������ߓx�̕���:


�����̏��ւ̑����ƂȂ�{

���H�I�ȏՓ˔���Z�p���L�͈͂ɃJ�o�[

�Փˍō��I
���R ��(������ЃZ�K)
�G�a�V�X�e��
����グ�����L���O: 2709
�������ߓx�̕���:


�Ǐ��ł��B

�v���O���~���O�͂ł��邪�Q�[���͍��Ȃ����Ȃ�����

�Q�[������肽������

��b���K�����ċÂ�ł܂������������ق���܂���

�����v���O���}����l�ŃQ�[���������悤�ɂȂ邽�߂̖{�B
���J ��N
�H�w��
����グ�����L���O: 151249
�������ߓx�̕���:


�N�H�[�^�j�I���̖{�H

7�͂����ʎ���

���ɓ�����Ǝv���܂��B

�{�������ŃN�H�[�^�j�I���𗝉�����͓̂���Ǝv��

�N�H�[�^�j�I����p�����R������]����̓K��
�x ����Y
�C��
����グ�����L���O: 382190
�������ߓx�̕���:


�����ɖ𗧂Ă�I�I�@������...
|
|
�I�� ���F
�O�b��
����グ�����L���O: 545133
|
Mark DeLoura �쐼 �T�K ��� �q�p
�{�[���f�W�^��
����グ�����L���O: 56751
�������ߓx�̕���:


�l�X�ȋZ�@���ڂ��Ă܂�

Graphics Gems�̌�p��

���~���͍�������

���{�̃Q�[���v���O���}�[��ڎw���l�Ɉ��
Mark DeLoura �쐼 �T�K ��� �q�p ���C �L�I
�{�[���f�W�^��
����グ�����L���O: 147427
�������ߓx�̕���:


Game�J���̎����I�ȑ��݂ł�
Dante Treglia ���{ �_ �쐼 �T�K
�{�[���f�W�^��
����グ�����L���O: 148533
Andrew Kirmse ���{ �_ �쐼 �T�K
�{�[���f�W�^��
����グ�����L���O: 157007
Kim Pallister
�{�[���f�W�^��
����グ�����L���O: 218804
Michael Dickheiser
�{�[���f�W�^��
����グ�����L���O: 190711
Scott Jacobs
�{�[���f�W�^��
����グ�����L���O: 188270
���{ �_
�{�[���f�W�^��
����グ�����L���O: 70836
�������ߓx�̕���:


���p�I�Ȏ�@���A���Z���x�������������Ǐ�
���{ �_
�{�[���f�W�^��
����グ�����L���O: 123436
Hubert Nguyen
�{�[���f�W�^��
����グ�����L���O: 29136
���� �_��
�H�w��
����グ�����L���O: 53313
�������ߓx�̕���:


���܂ǂ�

�����������Ȃ�c�����ł���

WEB�łƂقړ���

���发�Ƃ��ăI�X�X����
�� ���� ���� ���h
�R���i��
����グ�����L���O: 79965
�������ߓx�̕���:


�ŏ��̂P���ɍœK

���l�V�~�����[�V��������ɁB

3����CG�̋��ȏ�����

�����܂œ��发

����p��
OpenGL����ψ���
�s�A�\���G�f���P�[�V����
����グ�����L���O: 55645
�������ߓx�̕���:


�Җ]�̃o�C�u������ OpenGL 2.0�Ή��ŋA���Ă��܂���

�����߂ł��I
Dave Shreiner The Khronos OpenGL ARB Working Group
Addison-Wesley Professional
����グ�����L���O: 6786
���] �@��(������Ѓp���J�N)
�C���v���X�W���p��
����グ�����L���O: 1635
�������ߓx�̕���:


OpenGL ES �Ɉ���߂Â��Ă�������ł�

iPhone��Open GL�̍ŏ��̑��������

�q���g����R�̗Ǐ��ł�
Aaftab Munshi Dan Ginsburg Dave Shreiner �A�t�^�u�E�����V �_���E�M���Y�o�[�O �f�[�u�E�V�����C�i�[
�s�A�\���G�f���P�[�V����
����グ�����L���O: 5269
�������ߓx�̕���:


�����߂ł�
N2Factory
�\�t�g�o���N�N���G�C�e�B�u
����グ�����L���O: 193706
�������ߓx�̕���:


�킩��₷���ł�

���S�҂ɂ͗ǂ����e�ł�

������₷��

�ƂĂ��ǂ����发

���ɂ킩��₷��
�H�w��
����グ�����L���O: 203036
�������ߓx�̕���:


DirectX9 December 2004��

���S�Ҍ���
���c �ΗY
Northbrain
����グ�����L���O: 9949
�������ߓx�̕���:


�킩���Ă���l�����̃��t�@�����X�{

�V�T�O�O�̋Ɉ�
|
|
G. �|���A
�ۑP
����グ�����L���O: 41
|
![[�摜�Fsin�� cos�� tan��]](RotationDirection/SinCosTan-s.gif)
![[�摜�Fsin�� cos�� tan��]](RotationDirection/Atan2CrossDot-s.gif)


























 ���Z�ŏK�����e
���Z�ŏK�����e �������Ȃ̂Ŏd���Ȃ��Ƃ͎v���܂����E�E�E
�������Ȃ̂Ŏd���Ȃ��Ƃ͎v���܂����E�E�E



![3D�]CG�v���O���}�[�̂��߂̃N�H�[�^�j�I������\�u�x�N�g���v�u�s��v�u�e���\���v�u�X�s�m�[���v�Ƃ̊W��������! (I�EO BOOKS)](http://ecx.images-amazon.com/images/I/51HCS2E3WSL._SL160_.jpg)
 �N�H�[�^�j�I���̖{�H
�N�H�[�^�j�I���̖{�H










![GPU Gems 2 ���{��� �]�n�C�p�t�H�[�}���X �O���t�B�b�N�X��GPGPU�̂��߂̃v���O���~���O �e�N�j�b�N�]](http://ecx.images-amazon.com/images/I/51386X12S4L._SL160_.jpg)







![DirectX �Q�[���O���t�B�b�N�X �v���O���~���O Ver. 2.1 Vista [NextCreator] (NEXT CREATOR)](http://ecx.images-amazon.com/images/I/51JLfl%2BxZsL._SL160_.jpg)

