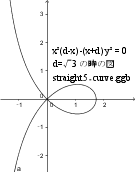二等辺三角形背中
©鳩摩羅童子 on 2011/09/22
下記の知的権利は全て鳩摩羅童子に帰属する。営利目的の使用を禁ずる。
二等辺三角形ABC の上に、それと合同な三角形A’B’C’を重ね、底辺両端の点B’, C’ を
斜辺AB, ACあるいはその延長部の背中上を移動させると、
頂点A’ の軌跡は、
点A を通る底辺BC と平行な直線となる。
【証明】
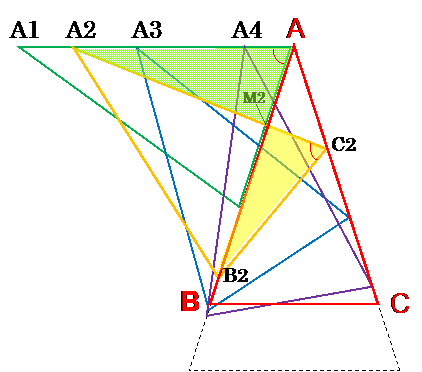
点A2 で解説する。△AM2C2 ∽ △A2M2B2 -- ①
(∵∠A = ∠A2, ∠A2M2B2 = ∠AM2C2 対角、で2角合同)
すると、△A2M2A ∽ △B2M2C2 が成立。
(∵①より、辺A2M2 は辺 AM2 に対応し、長さ比は相似比。辺 B2M2 と 辺C2M2 の関係も同様。
すると、相似の「2辺比相似&侠角合同」が成立し、相似成立。)
すると、∠M2AA2 = ∠M2C2B2 = 二等辺三角形の底辺の角。
つまり、点A2 は、線AA1上に常にある。
《補足》
辺 B2C2 が △ABC の背中を跨いでこすっているが、視点を変えると、
線分 B2C2 の両端を 角BAC の股がこすっている、とも見える。
点A の軌跡は、線分(= 弦) B2C2 から見て、円周角一定の軌跡であり、円を描く。
つまり、△A2B2C2 から見ると点A は、外接円上にあり、 △A2B2C2 の外心から距離一定。
(点A から見ると、三角形の外心の軌跡は点A を中心とした円弧を描く。)
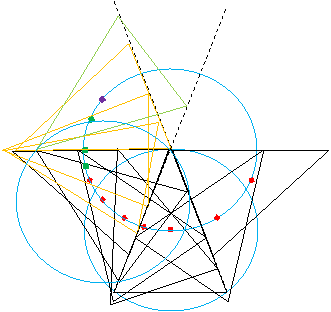
・ 下図は、外接円と、外心の軌跡と、の図。
【チェビシェフ・リンクによる歩行器の実装法】 --- 重要度が高いので、最後に掲載していたものをココへも copy した。 DEMO
胸を張って宣言する。
下記は、チェビシェフ・リンク使用歩行器の世界で最もシンプルで、かつ、実用的な実装法である。
(チェビシェフ・リンク機構は、歩行ロボットの足のきれいなカマボコ状軌跡を提供するが、クランクの下では無く上方に軌跡が出来るのが、玉にキズ。実装はこの軌跡を下へ移動させる必要が有るが、ヘタをすると、その為に元の3本より多くのリンク棒を必要とする。困ったもんだ。の問題が有った。)
発見者は私。--- 昔から散々考察しているにもかかわらず下記の解は出て来なかった。が、2018/01/23 に、有る拍子に、ポロっと出てきた。恐らく、世界初の実装法である。
(web 検索して、既存の方式か否かを確認したが、この例は無かった。なので、新規性を有する。)
(他の方式も名前が付いているので、真似して名前を付けた。「Chebyshev X Linkage」 と名付ける。)
cf. Chebyshev's Lambda Mechanism (wikipedia)
cf. Klann linkage (wikipedia) [including Jansen Linkage animation, too. ] -- これらは、所詮、非実用解だと思う。
cf. Leg mechanism/ Gallery
--- 9 種の方式が記載。しかし、やはり、下記には負ける (?)。
cf. CATIA - Theo Jansen's mecha based system (YouTube) --- 面白い。
■通常、茶色の水平棒は長くして、先頭とお尻に垂直な脚を設けるので、6 bars 化は全く不用。
 - Chebyshev_X_Link.png -
- Chebyshev_X_Link.png -
BC // C'B' and,
△ABC ≡ △EC'B' , so, EB' // AC
Very Good !!!
Geogebra のサイトに登録した。
動作確認したい人は飛んで。 DEMO.
老婆心:
通常は EB' // AC が保証されるが、
∠BAC or ∠C'EB' が 180° or 0° 直後、
ノード E が誤った側に折れる懸念がある。
従って、もし必要なら E にガードレールを付けよ。
足に踵(かかと)を付けるのも q の垂直性保持に有効。
(E の軌跡は、チェビシェフ・リンク曲線である。)
青色の bar を追加しても良い。但し全体で6 本となる。
但し、青色実装も案外難しい。
AB 不要と成る (回転軸 A ▲ 不要。 スバラシイ)。
チェビシェフ・アメーバ/チェビシェフの八角形
(8角形車輪) Octagon wheel
「ルーローの三角形」と言う名前があるので、この図形を「チェビシェフ・アメーバ」と勝手に名付けることにする(発案者の特権である)。
「ルーローの三角形」は有名だが、この「チェビシェフ・アメーバ」には負けると思う。なぜなら、実生活において、このアメーバは、ルーローの三角形よりも、はるかに有用であることは自明だと思われる。
床の上に置いて荷重を掛けた場合、このアメーバの身体の中心(軸)の高さは、ほぼ一定[誤差 0.24% 以内]である。車輪の代用に成る。
(また、軸は、角度に対し、ほぼ等速で移動する[誤差 5% 以内]。)
チェビシェフ・リンクを隣接して輪にしたもの。
アメーバ状の凸八角形になる。新しいキャタピラー機構である。 on 2018/02/22
かなりシンプルで、面白い実装法。かなり賢い機構だと思う。
Geogebra のサイトに登録した。
動作確認したい人は飛んで。 DEMO. ---- お遊びして下さい。
cf. 軟弱地盤に特化した走行系の形状及び表面性状に関する検討
--- 私の八角形車輪もテストして欲しい。また、下駄を履かせた八角形車輪 もやって。
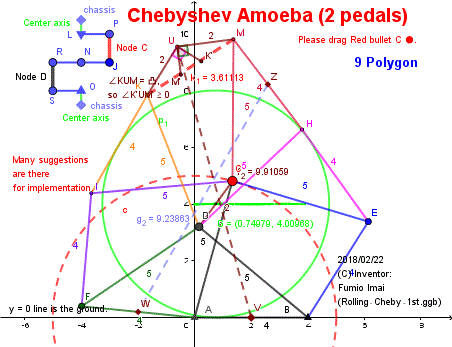
チェビシェフ・アメーバ
Chebyshev Amoeba
左記の九角形がルーツで、実装は色々な変化が可能。
(2pedals 方式は、軸周りの部分の実装に難がある。)
最新・詳細は、Geogebra を見て下さい。
--- 最終的には、八角形車輪の実装で決着した
(次図の Last model)。
on 2018/04/03
世界初 八角形車輪
恐らく世界初の八角形車輪です。 ---- チェビシェフ・アメーバ 最終モデル on 2018/04/13 記載
(前図の 2 pedals 方式と等価な 1 pedal 方式で、リンク棒の衝突が無い優れた実装法である。
--- ブッチャケタ話、前図の車輪は造るのが難しい[特に軸周り]が、下図の車輪は造るのが簡単である。 )
[ Chebyshev linkage と Chebyshev's Lambda Mechanism との実装法の関係と似ている。 ]

360°を チェビシェフ・リンクで分割すると、
常に、7 個+分割 gap (可変長)となる為、
8 個のうち、
対角の2 個を閏月(うるうづき[補正月])とする。
(閏月は動的に完全月にするが、完全月にすると、
その閏月が無くなるので、閏月は最低2個必要。)
閏月のチェビシェフ・リンクの辺 は 1+1 の
折り曲棒 bent-bar(可変長の辺)である。
完全月のチェビシェフ・リンクは 2, 2.5, 1, 2.5 の 4 bars。
閏月は、(1, 1) , 2.5, 1, 2.5 の 5 bars である。
閏月対応の外周の edge が地面接地に関与する場合、
1+1 の bent-bar は直線化され、最大長 2
に自動的になる仕掛けになっている。
自重による地球の引力によって制御されている。
Chebyshev Amoeba (= Chebyshev linkage loop)
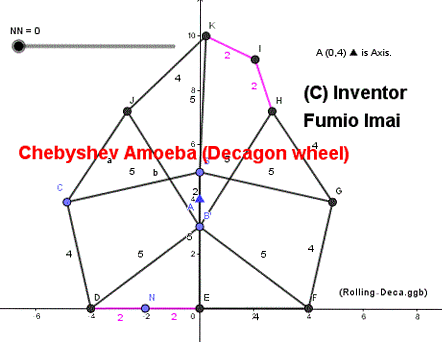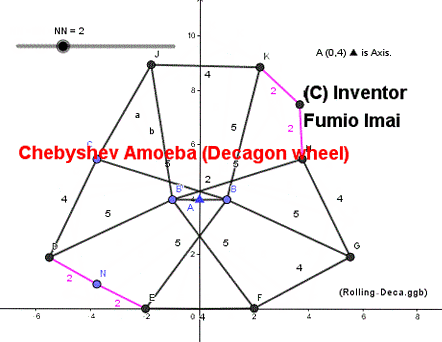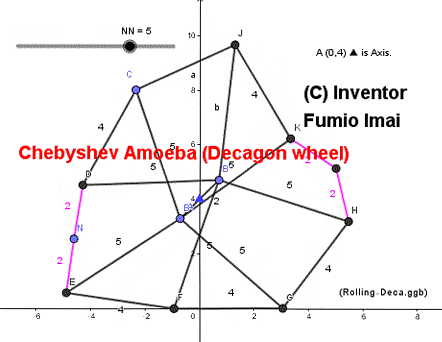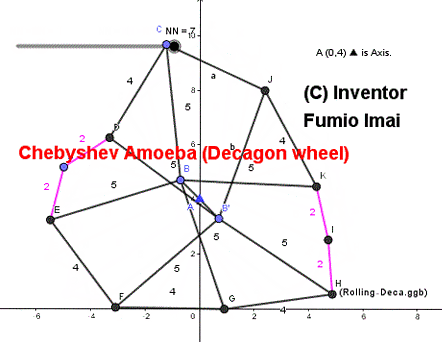
Google Photo で gif animation を作った。
ペダル1回転の分をループさせている。
(実際にはペダル4回転させないと、外周は1回転しない。)
この gif animation (Rolling_Deca_anime.gif) の file size は、
168 KB だった。
YouTube 用に .avi 変換したら、 size は 3,551 KB
に跳ね上がった。
cf. https://www.youtube.com/watch?v=WO2sNLa7N0M
[YouTube の見栄えは、今一、で良く無い。]
左図をよく見ると、
ピンクの bent-bar の角度は、イイカゲンで、
車輪の上半分は、ブラブラ状態である。
しかし、bent-bar は、両端の縦線がクロスし、
しかも、bent-bar 自身が地面上のときは、角度は 180°である。
(bent-bar の終端間の距離は、約 3.5 から 4.0 である。)
このアニメ、見ていて飽きないね。
何か、馬が優雅に歩いている様で、癒やし効果がある (?!)。 --- bent-bar があった方が躍動感が出て良い。
このアニメ画像は、自由にコピペして良い。作者の私が許す。--- 日本の常識、平成の常識にして欲しい。 on 2018/05
-----
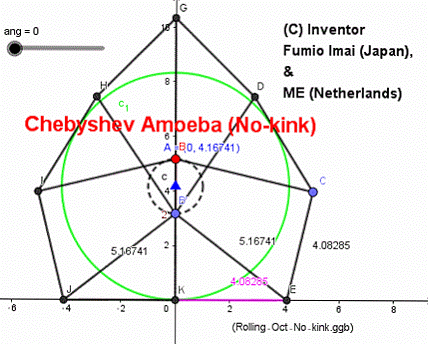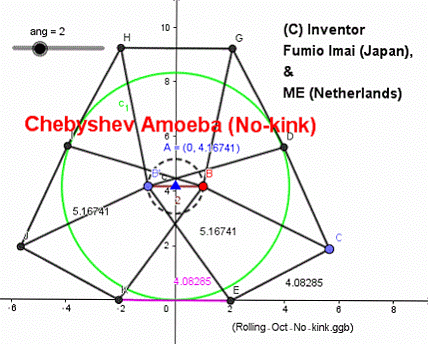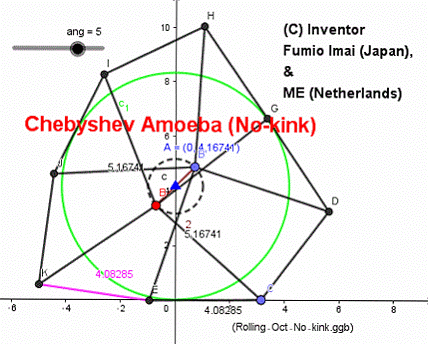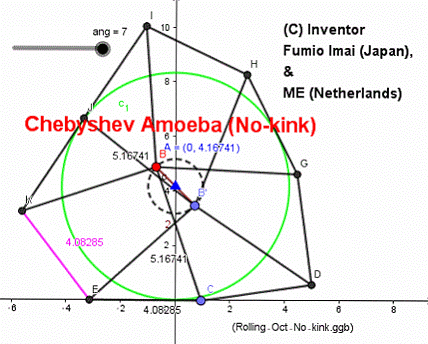
左図は、
海外の車輪サイトに投稿しておいたら、オランダの人から
bent-bar が無い比率のサンプルを提示された。
チェビシェフ・リンクの疑似直線性の誤差が少し落ちるが、
実用レベルには支障無い。
また、ピンク色の部分の長さは変化するが、極微であり、固定長とみなして良い。
GeoGebra の Rounding: 15 Decimal Places 機能の 15桁丸め誤差数値を指定し、
この比率でシミュレートすると、外周1回転でのギャッブの可変の辺の長さのブレは、
4.082845933118707 max,
4.082845933118416 min,
0.000000000000291 err order
誤差が 0.000000000000291 ということは、きしみの心配もしなくて良い。
( 誤差が小さ過ぎるのが異常である。よく考えると、この比率を求める為にペダルの角度がゼロの図を利用したが、ロジック的には、角度に依存しない (実は、???)。なので、常にギャップ値が固定になる比率が存在し、これがそれである。)
Tue Apr 17, 2018
Mr. "ME" (Nederlands) suggested me a below ratio.
-- Gap length ≒ constant ratio --
Inner radius: 1 (or axle diameter 2)
Edge-length ee: 4.082845933119... (= sqrt[rr2-(rr-2)2] = 2 sqrt[rr - 1] )
Radial-length rr: 5.167407728397...
-----
axle trace is almost line.
height: -- err order is < 0.015/4 (= 0.37%),
min 4.16741 (x=0)
min 4.17754 (x=2)
max 4.18217 (x=1)
[ Original Chebyshev linkage 2:4:5:5 bars
height is from 4.0 to 4.00975 ,
err order is < 0.00975/4 (= 0.24%) ]
■ bent-bar アリ、ナシ、どちらの車輪が良いか?
個人的には、bent-bar アリの方がシンプルで好き。軸の軌跡の直線性も良い。整数比の長さの方が作るのが楽。ソモソモの原理を解説している。八角が十角になるのが少し難(但し、実装はどちらも同じで、内部 clone 内に bent-bar があるか、無いか、の違いだけである。なので、技術的には、bent-bar 無しにするメリットは全く無い。 逆に、bent-bar が無いと温度差による棒の長さの変動による軋み(きしみ)が問題になると思う。)。
■ rr の数学的解析 by らすかる氏 cf. DS 数学 BBS・2 on 2018/04/27
らすかる氏によると、ペダル角度がゼロの左右対象で、ローマ法王の冠の様な図形、の時は、
ee = 4.08284593311934118466290274562471952834199482221455...
rr = 5.16740772839728595747372780506339609865810833312219...
の 50 桁近似数値だそうな。 また、rr は、下記の 5次方程式の5個の根の中の最大解とのこと。
x5-2x4-16x3-16x+32 = 0 ---①
【尚、この式は、x=2t、とすると、t5-t4-4t3-t+1 = 0 ------①' と等価】
c. 私の代数解析によると、①は、
x8 -32x6 +160x4-128x3+256x2-512x+256
= (x-2)(x2+4x-4) (x5-2x4-16x3-16x+32) = 0 の結果に他ならない。
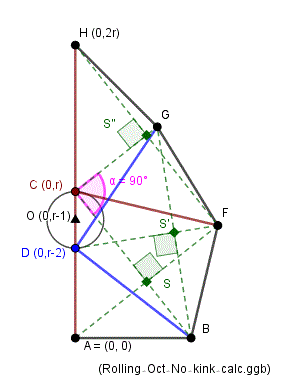
Analytical calculation. --- r tuning.
C= (0, r), D = (0, r-2), H = (0, 2r), A = (0, 0)
B = (sqrt(r2-(r-2)2), 0) = (2 sqrt(r-1), 0)
F = (4r2sqrt(r-1)/(r2+4r-4), 8r(r-1)/(r2+4r-4) )
x(G) = [-2 (r-2) t -2 sqrt(r-1) (t2 -1) ] / [t2 +1]
y(G) = ( r3 + 2r2 +4r -8) / {r2[t2 +1] }
here,
t = (-r3 + 6r2 +4r -8) / [4r2 sqrt(r-1)]
t2 +1 = (r6 +4r5 + 12r4 +64r3 -80r2 -64r +64) / (16r5 -16r4)
CG ⊥ CB ---- So, inner product = 0
↓↑
r8 -32r6 +160r4-128r3+256r2-512r+256 ②
= (r-2)(r2+4r-4) (r5-2r4-16r3-16r+32) = 0 ③ ----- This is the answer.
よく分かりませんが、8角形なので 8 次方程式なのかも知れません。
8 次が更に、1次、2次、5次に因数分解されるのも予想が付かない。他の人の答えが 5 次だったので分かったが、一人でやっていたら気が付かない。
■ もう一つの ee, rr 比率
軸の高さのブレが小さいチェビシェフ・リンクとして、4:5:2 の比率以外の比率の解析解が存在する(長さ2のペダル棒の角度が、垂直の時と、水平の時とで、それぞれの中点(ペダルの軸)の高さが、等しい、の条件を満たす解である。4:5:2 の標準では、ペダル棒が垂直の時、左のクロス縦バーも垂直だが、汎用解は、左の縦バーは垂直では無く、傾いている。地面と直角では無い。)。 それを適用すると、
ee = 4.309198068172...
rr = 5.473214075856918...
の八角形も有力な解である。高さのブレの誤差は、 4.47085 to 4.47694 --- under 0.14% [+ 0.00609/ 4.4 err order] で、何と 4:5:2 の標準のチェビシェフ・リンクのブレ誤差 (0.24%) よりも直線に近い。
但し、しわ寄せとして、地面の足元の2毎枚板の角度が 180°では無く、177.41°であり、少し上り坂になっている。なので、次の板に乗り換える時、3°の傾きの上に乗ると、重みですぐ 0°の傾きになり、今までの板が 0°から 3°と傾く。つまり、ギッタンバッコンが発生する。この時、軸は棒高跳びの半径の棒が約 3°回転する様なもので、少し上に上がり直ぐ下がる。 3°なのでこの変化は極微である。
内接円が、3°回転し、軸が、同じ高さで「高さ×3°」前に移動する形に見える。
このとき、板の継ぎ目は 3 °の角があるので、地面には下駄で歩いた様な跡が残るかも知れない。
(跡が残るかも知れない。は、ウソかも。∵ 0°/180°の前後 ε°でも高さは変わらないので、板は、軟着陸するカモ。)
また、農業用トラクターなどでは、逆に角が有った方が良いかも知れない。また、下駄で道を歩くのは禁止されていない。
地面の隣接する辺の角度が 180°で軸の高さのブレが悪い (誤差 0.37%) のと、 177°だが高さのブレが悪くない (誤差 0.15%) 、のと、どちらが良いか。頭が痛い。 --- 誰か教えて欲しい。 → 両方共、一長一短があり、両方共良いと思う。
良く分からないが、177°角張っているということは、360°を 3°単位に分割し、円を 120 角形 (360/3=120) で模擬したのと同じの意味かも。だとすると、120 角形はの高さのガタは、半径を r とすると、r と r×cos(3°)の誤差、つまり比の精度は、 cos(3°) = 0.9986295 = 99.86295%の精度、0.1370% の誤差。瞬間的にこの分上がって、すぐ戻る。高さのブレ 0.15% とほぼ同じ。
--- 5:4:2 比の普通のチェビシェフ・リンクの誤差 0.24% よりも良い。問題ナシ。
(チェビシェフ・リンク機構の疑似直線性は、対角の長さ 5 のバーがクロスしているとき、ほぼ高さ 4 で長さ 2 のペダル棒の中点[ペダル軸]が移動する、のが、特徴。
この軸の軌跡は、カマボコ状で、底辺がほぼ水平である。この水平部分のペダの角度は 0°~180°はもちろんであるが、その前後の少しのマイナス ε 角度分(5 のバーはクロスしていない)も水平を維持する [-ε°~ (180+ε)°]。前述の 177.41°はこのマイナス角度内であり、高さ一定範囲内である。)
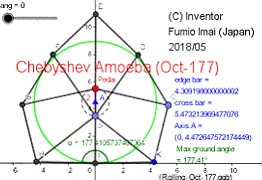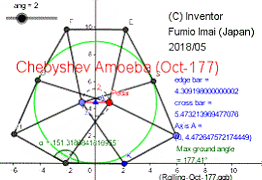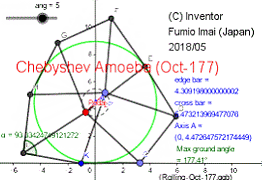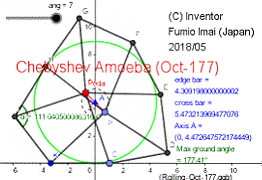
・八角形車輪
・地面を踏む辺の切換時は、 120 角形の 177°の角度の角(かど)を持つ。
(しかし、車輪板は軟着陸し、床は傷つかない。)
・ペダル軸の疑似直線性の精度は、通常の 4:5:2:5 比のチェビシェフ・リンクより良い。
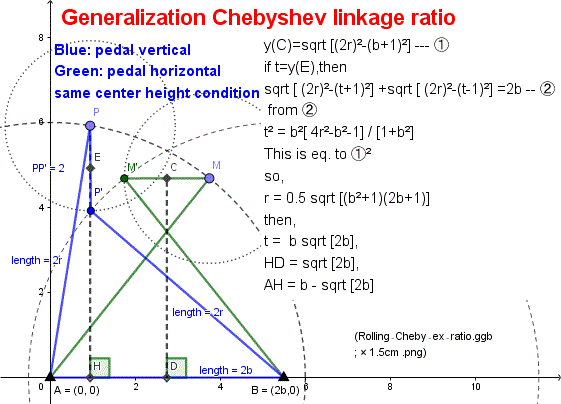 チェビシェフ・リンクの棒の長さの比 4:5:2 の比は、ペダルが垂直から 180°回転する時の 0°, 90°, 180°のペダル角度の時の中点の高さが等しい為に、ほぼ直線に見えるカラクリになっている。
チェビシェフ・リンクの棒の長さの比 4:5:2 の比は、ペダルが垂直から 180°回転する時の 0°, 90°, 180°のペダル角度の時の中点の高さが等しい為に、ほぼ直線に見えるカラクリになっている。
底辺とクロスバーの長さの比率を変えてもこの3点条件を満たせば、直線近似描画は可能である。
ペダルバーが垂直の時、クロスバーは垂直では無く、台形の形を構成する様になる。
Tip:
左図でペダルが右回転するときは、E は右に移動する。これはイメージ出来るが、左回転するときは、どうなるか。慣性がある場合、左に移動する。但し PA を左に押しつつ、PP' が左回転するため、外目は、PP' は垂直のまま左へ並行移動している様に見える。B は、A を軸に左に回転し、持ち上がる。 E は、P の円の真上の円弧の軌跡と並行な軌跡で、-AH の反対側まで、棒高跳びの軌跡の様に移動する。多分。
従って、E の水平軌跡のブレは有る。が、チェビシェフ・リンクの直線性の誤差と同等であった。
ex. b=2 の時、
2b= 4, 2r = sqrt[(b2+1)(2b+1)] = sqrt[(4+1)(4+1)]= 5
算出式:
中間のペダル水平の時、
y(C)=sqrt [(2r)2-(b+1)2] --- ①
開始と、終了のペダル垂直の時、
if t=y(E),then
sqrt [ (2r)2-(t+1)2] +sqrt [ (2r)2-(t-1)2] =2b
sqrt [ (2r)2-(t+1)2] = 2b -sqrt [ (2r)2-(t-1)2]
[ (2r)2-(t+1)2] = 4b2-4b sqrt [ (2r)2-(t-1)2] +[ (2r)2-(t-1)2]
4b sqrt [ (2r)2-(t-1)2] = 4b2+[ (2r)2-(t-1)2] - [ (2r)2-(t+1)2]
4b sqrt [ (2r)2-(t-1)2] = 4b2 + (t+1)2-(t-1)2= 4b2+4t
b sqrt [ (2r)2-(t-1)2] = t+b2 --- ②
b2 [(2r)2-(t-1)2] = t2+2b2t +b4
b2[4r2-t2+2t-1] = t2+2b2t +b4
[1+b2] t2 -4b2r2+b2+b4=0
t2 = b2[ 4r2-b2-1] / [1+b2] 【1次項 t, b, r は何故か全て消えた。 why?】
This is eq. to ①2,
t2 = b2[ 4r2-b2-1] / [1+b2] = [(2r)2-(b+1)2]
b2[ 4r2-b2-1] / [1+b2] = [4r2-b2-2b-1]
b2[ 4r2-b2-1] = [4r2-b2-2b-1][1+b2]
4b2r2-b4-b2=4[1+b2]r2 -b2-2b-1-b4-2b3-b2
4(b2-b2-1)r2=+b4+b2 -b2-2b-1-b4-2b3-b2
4(-1)r2=-2b3-b2-2b-1=-b2(2b+1)-(2b+1)=-(b2+1)(2b+1)
∴ r2 = (1/4) (b2+1)(2b+1)
r = 0.5 sqrt [(b2+1)(2b+1)]
ちなみに 高さ t2 = [(2r)2-(b+1)2] = (b2+1)(2b+1)-(b+1)2 = 2b3+b2+2b+1-b2-2b-1= 2b3、つまり、 t= b sqrt(2b)
また、 AH = sqrt[(2r)2 -(t+1)2] = sqrt[ (b2+1)(2b+1) - 2b3 -2 b sqrt(2b) -1] = sqrt[b2 +2b -2 b sqrt(2b)] = sqrt[(b-sqrt(2b))2] = b-sqrt(2b)
また、HD = b-AH = sqrt(2b)
【あるいは、 ② から、HB = sqrt [ (2r)2-(t-1)2] = (t+b2)/b = b + t/b= b+sqrt(2b) --- = 2b-AH ∴ AH = b- sqrt(2b) でも良い】
Hart-A Amomeba, Peaucellier Amomeba
チェビシェフ・アメーバの概念を擬似直線器では無い純粋直線リンク機構である Hart's A-frame や Peaucellier linkage に適用すると、5角形以上のアメーバ車輪が簡単に実現できる、と判明。
しかし、色々やってみると、ポースリエは、モータ駆動は NG (等速化ペダルができない)。手押し車専用。
等高さとしてのルーローの三角形なんて、多角形アメーバに比べればクソである。
AC と並行なペダルを設定すると、等速移動できる。K に AC // D'DD'' // KP なる 並行リンク機構を付加し、 P をペダルとする。 C'JA は、C'J と並行なリンク機構で模擬(辺の数だけペダルを用意しない。地面対応のペダルは、C'JA は直線になっており、複数ペダル中正しいものは必ず1つある。引っ掛けて回していれば、その一つを間接的に押しており、エッジは回転する。連続的に地面のエッジ切替わるの、恐らく速度の等速性は成立する。)。
ハート A は、5角形で内部バーがエッジ外にはみ出る。また、地面のと辺の角度が 90°以下だと、端の直角棒がはみ出る。なので、6角はOK。(半径1の内接円、エッジは2の長さ。底の2辺が180°、和4のときは。横長長方形。4×2。 可能な変化をみると、トラクタや戦車の様な横長の車輪の動きとなる。面白い。6角の場合、常にどの角も90°以上を維持できる。なので、垂直棒もハミ出ない。チェビシェフだと無理。→ なので、Hart-Aの垂直柱も、エッジの中点に立てる。)
また、7, 8 角だと周の内側が棒ダラケで実質NG みたい。
ポースリエの方がエッジの中点に垂直棒があるのでコンパクトで、対象性があるので外へははみ出ない。
しかし、駆動車輪には出来ない。
---- 世の中、うまく行かない無い。
c. 軸は share するが、ペダルは share していない。8個のペダルが放射線状になっていて、角度も可変。しかし、1個のペダルを駆動すると、全体は引きずられる形で回転する。
チェビシェフ・アメーバもこうすると、gap のエッジは最初から存在しない。 ben-bar のからくりも不用。 --- simple さが崩れるので止めた。
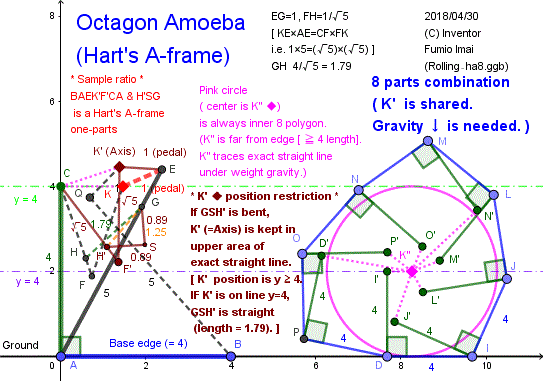
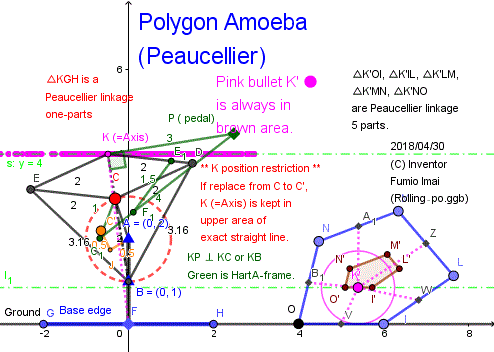
K' の駆動ペダルとしては、代表エッジを1つ選び、その K'Vの方向もどきを常にペダル方向する。簡単である。
KB (つまり、KC。∠EKD の二等分線) と直角な固定長のペダル棒と、Hart-A の3本の green バーを KD, DB に追加するだけ。
典型的な Hart A-frame 作図で、比率計算も容易。 Peaucellier & Hart チャンポン製品。
非常に相性が良い。
(左記の右半分の、ピンク破線 ・・・ がペダル対応の角度であり、エッジが地面外でも連続して回転している、ペダルは外周1回転で1回転であり素直である。チェビシェフ・アメーバの八角形のペダルは、8回で外周1回対応であった。)
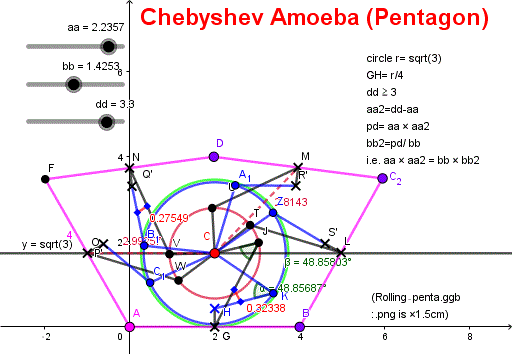
■ Pentagon wheel 五角形車輪 サンプル
五角形車輪 も容易に作成可能。
四角形車輪は、2辺が 180°のとき、上下ペッタンコにつぶれるため
不可能。
五角形以上なら可能。但し、軸の水平起動維持のための
チェビシェフ・リンク機構は、八角形以外のケースでは、水平近似が
崩れるため採用不可。
完全直線描画リンク機構を使用するしか無い。
ポースリエ・リンク機構でも良いが、バーの本数が多過ぎるので、不向き。
ハートAフレーム機構 (Hart's A-frame) が最小本数で良い。
実装のサンプル図を示す(click すると鮮明図が見れる)。
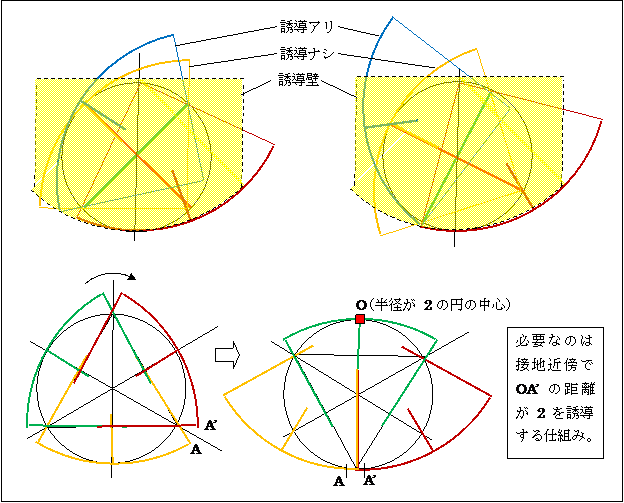
赤色の軸 C ● は、ピンクの外辺から、常に 距離 r 以上離れていることが保証されている※。
重力下の下では、軸は地面から r の水平位置を移動する。
ピンクの壁面は押されて転がっていく形になる。
※ ◆-◆ の「カスガイ棒」を「一本棒」では無く「折れ線棒」にすると実装される。
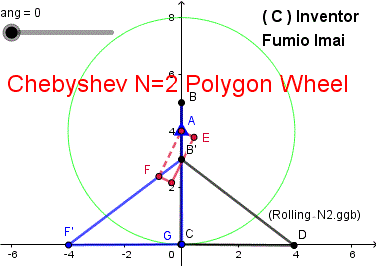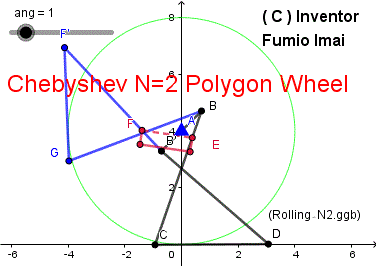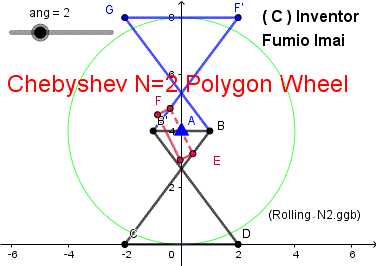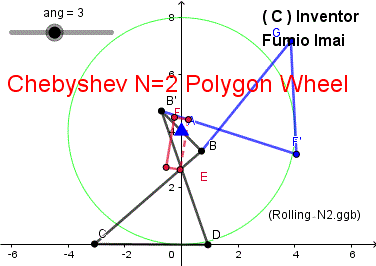
■ N2 Polygon wheel
最もシンプルな棒だけの車輪。
簡易荷車用車輪。
Geogebra 解説& DEMO サイト
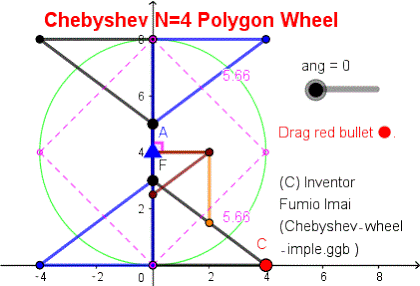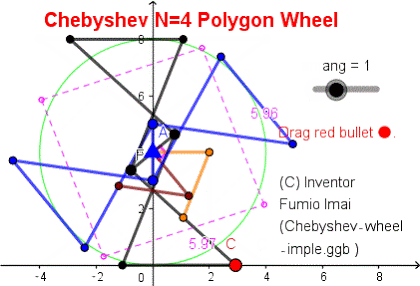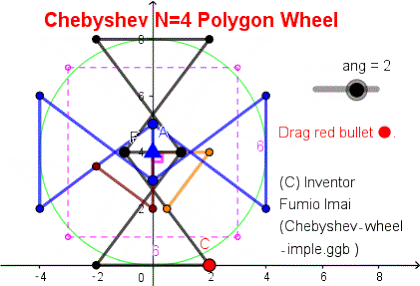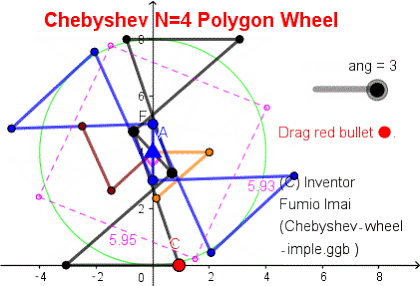
■ N4 Polygon wheel
棒だけの N=4 車輪。
簡易荷車用車輪。
Geogebra 解説& DEMO サイト
【特注】 教育的指導。 on 2015/12/13
任意の三角形 △ABC(対辺を a, b, c とする)は、辺 b, c が固定長で、∠A の角度を色々変え、底辺 a の長さが伸縮する image を想像して下さい。
相似の子供を2つ内包する。
∠A が直角のとき、 a2 = b2 + c2 が成立。
---------
等積ツール(逆数入手装置、反転器)の件。
長さ BA' = c × (c/a) = c2/a
で、この値は、a の逆比例であり、
可変長 BC の逆数の長さを自動生成する装置として利用できる。
BC×BA' = c2 = 一定
しかし、点 A' の位置を自動的にポイントするリンク機構は、一般に、思いつかない。
しかし、垂線の足である点 H (Horizontal の H) は、少し違って、この特別な性質の点は、辺 c の中点から 0.5 c の長さの棒と、辺 b の中点から 0.5 b の長さの棒があれば、自動ポイントされる。
よく似た、特別な点として、中点 M (Middle の M) の位置がある。
辺 c の中点から 0.5 b の長さの棒と、辺 b の中点から 0.5 c の長さの棒があれば、自動ポイントされる。
さてさて、これで準備 OK である。
左図をにニラメッコすると、
底辺両端の2点から垂線の足までの距離の差と、底辺との積は、一定。( ∵ BH - HC = [BA' + t] - [t + A''C] = BA' - A''C = c2/a - b2/a = (c2 - b2)/a) ---- ①
[ここで、A'H = HA'' の長さは、は変数 t とした。しかし、t は相殺し合って全面に出ない。]
しかし、この性質は、装置としては利用しにくい。
(ほぼ等価の、2 BH -BC、でも +2t -2t で、t は相殺される [ i.e. 2(c2/a + t) - (c2/a +b2/a + 2t) = (c2-b2)/a]。これはポースリエの反転器である。しかし、リンク数は6本。)
中点と垂線の足の距離の差を考える、(左側から見るとする)
BM = 0.5{ BH + HC } = 0.5{ [BA' + t] + [t + A''C] } = 0.5{BA' + A''C} + t = 0.5 (c2 + b2)/a + t
t が邪魔であるが、垂線の足までの距離、左側の BH = c2/a + t との差をとると、やはり相殺されて消える、
i.e. BM - BH = [ 0.5 (c2 + b2)/a + t ] - [ c2/a + t ] = 0.5 (- c2 + b2)/a
つまり、中点と垂線の足の距離の差と、底辺との積は一定。
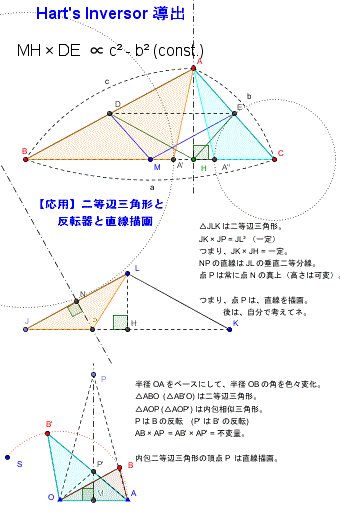
左図で、点 D, E は中点とする。
ハートの反転器のリンク機構(青と緑の蝶々の羽の形の棒)は、4本の棒構成である。ポースリエの反転器は6本である。
数学者のハートの方が軍人のポースリエより、やはり、センスはかなり良い。
尚、この装置は b = c の二等辺三角形の場合無能であり、適用外である。
二等辺三角形の場合の 点 A' は、辺 c の中点 D からの垂直二等分線と底辺 a との交点である。(左図の真ん中) [誤]JK × JH = 一定。 [正]JK × JP = 一定。
ボヤケて見えない所、は、 --- つまり、点P は、直線を描画。
しかし、装置化はやはり出来そうに無い。(try してみて下さい)。
反転器は、円軌道を直線軌道に mapping するツール(描画システム)として利用される。スライダーの摩擦無しに完全直線を実現する(摩擦は、アームの回転軸の回転摩擦のみ。)
c = b の二等辺三角形の場合、反転器は構成出来なかった。しかし、この特殊環境は、直線器作図の環境を提供する。
下2つの図は、反転器の応用である。
この図において、JL の床に居る N から見て、P は常に真上にある。
(∵ 点 P は、N からの JL の垂直(二等分)線と 直線 JK との交点。)
JP, JH の 点 J, P, H の3点(あるいは、点 J, P, K の三点)の位置関係を反転器で規制し、距離 JH (または JK) の長さを変化させると、
JP の長さも同期して変化、しかし、P は N の真上。
結果的には、JL, LK の二等辺三角形の固定長の棒の背中の片方の JL を床に固定し、もう一方の背中の棒 LK を点 L を軸にギコギコ回転させると、点 P は、床に対して垂直な直線を描く。
( あるいは、LK の棒は取っ払い、NH に 0.5 JL の長さの棒をかます [∠JHL = 90° は維持される]。
でも良い。)
点 K ( or 点 H) は円を描く。点 P は直線を描く。 つまり、5本の棒があれば、擦らず(こすらず)、完全な直線を描画できる。
【 ハートの反転器の外形は左右対称台形であり、下底と上底は、一直線上に無い。
しかし、上底と下底との、間又は外に、平行線を引き、棒との4つの交点に印を付けると、その4点は一直線上にあり、2点間の距離は、上底、下底の長さに固定比例している。 】
-----------------
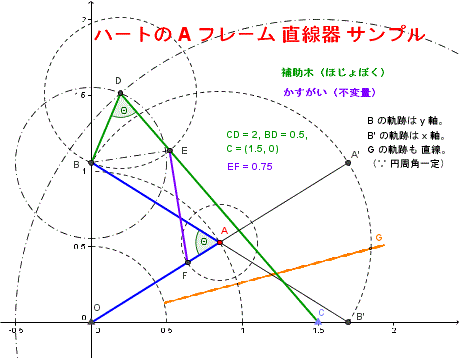
ハ-トさんは、 Hart's Inversor の発見・定義者であるが、 Hart's A-frame という反転の原理ではない直線描画システムの提唱者でもある。
固定長の棒の両端を x 軸, y 軸に乗せ、こすると、棒の中点は、円を描く(直径の円周角は 90° で一定の応用)。つまり、円を仲介とした、直線から直線の mapping である。
こするので、この機構は直線描画システムでは無い。
しかし、これを少しイジり、動作の自由度を減らすと分かり易い直線器が得られる。
左図は、A-frame のサンプルである。緑色の棒の形状は、青色の棒の条件に依存し、解は無限にある。
① 「青の2辺の積 = 緑の2辺の積」とする。---- 1*1 = 1 なので、(1/2) と 2 [(1/2)*2 = 1] を選んだ。
② ①を満たすと、最終的に、青棒の狭角と緑棒の狭角の値を常に同じにする効果がある(図中のΘ)。
③ 緑棒の根本の x 軸上点 C の位置、は、Θの初期値に依存。例えば、Θ = 0 ° [2辺がぺッタンコ状態]のとき、青色の先の点 B は (0,0) なので、点 D は (-0.5, 0) となるので, C (-0.5+2, 0) = (1.5, 0) が自動的に誘導される。
[緑棒のΘは、もう、青棒のΘに完全依存状態で、常に等しい。例えば、Θ = 180° を確認すると、B は (0, 2) にある。 (0, 2) と (1.5, 0) の距離を計算すると、 22 + (3/2)2 = 4 + 9/4 = (16 +9)/4 = 25/4 = (5/2) 2 = (2.5)2 なので、緑棒が、まっ平らになって、長さが 2 + 0.5 = 2.5 になった状態と一致する。]
③ この A-frame システムは、再帰システムであり、recursive な 、ある種の feedback 制御機構である。自分の中に自分の分身を含む。青と緑をつなぐ紫のかすがいは、線分 OC の基底の分身である。 -----△COB を裏返しして、縮小させて、回転させると、△FEB になる。頂点 B は共有。
【 汎用の y 軸直線描画の A-frame では、青の根本は、(0,0) では無い x 軸上の点。又、青の2辺の比も 1:1 では無い。しかし、この A-frame 環境にすれば、楕円等は簡単に描画できる(ex. 直径 BB' 上の固定点の軌跡)。】
---
c. 「点G の軌跡も 直線。」って、図中に書いてあるが、後になってから見たら、意味不明であった。解説不足なので、補足する。点B' は、B の線分AB の 180°回転反対側である(BB' は直径)。点B の軌跡は x 軸。点G は、任意の 180°でない分 AB を回転させたB 対応の点である。△BAG の板を作り(BG は弦)、点A● を動かすと、点 G は、∠BOG の円周角(∠BAG は中心角)が一定角度の直線軌跡を描く。という意味である。
【応用】
■ 凸凹道と四角い車輪
■ 凸凹道と五角形車輪
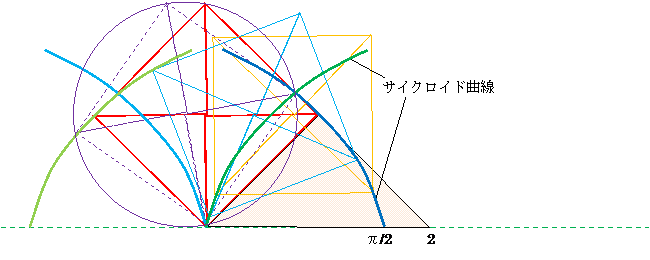
■ 四角い車輪(通常のサイクロイド曲線の凸凹の場合)
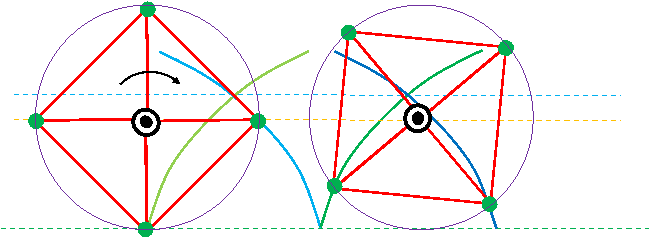
■ 四角い車輪回転の端点トレース
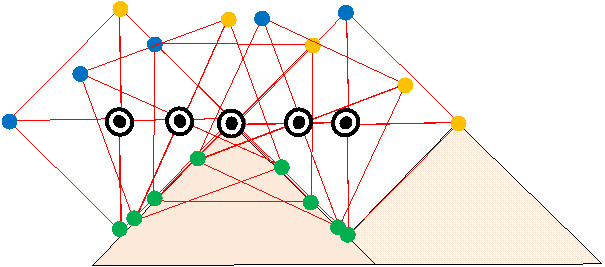
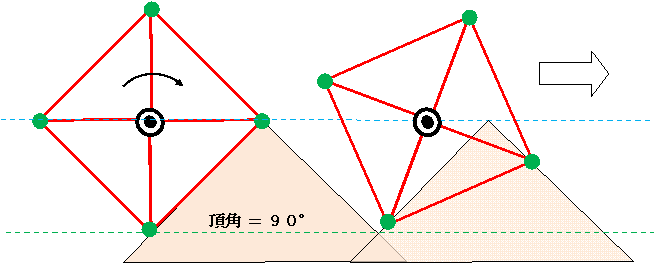
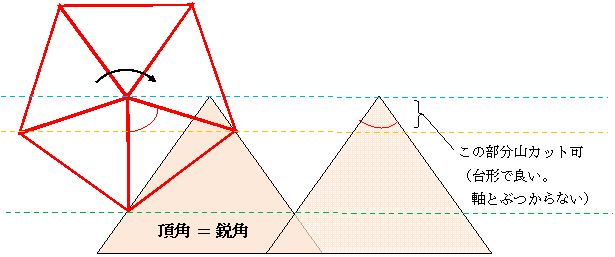
■ 平坦路と「3つの提灯ピラミッド付き十字架車輪」 (凸凹道路を自前で持つ四角い車輪)
《解説》
十字架の4つの端点は、谷底で隣の山に切り換わる。
例えば、
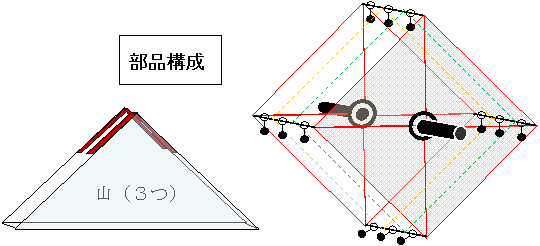
山は左右二面の板を隙間を開けて接合する。山の頂上内側2面には各々屋根(or 軒)を左右に設ける。
屋根と屋根の間には隙間を設ける。[屋根は図中茶色]。
2面の山の背をこする端点(端点棒)の中央に、ひも付きボール(錘)をぶら下げる。[図中、ひも付き黒玉]
端点が頂上に来たとき、ひもは左右屋根の間を通り抜け、ボールは屋根の真下にある。
端点が頂上から上へ飛び立つとき、ボールは屋根の隙間に引っ掛かり、山をぶら下げる形となる。
また、浮いた山は着地点で、着地直後ボールは屋根から離反し、端点と頂上の従属関係は切れ、
その端点は、山の頂上から下る状態となる。
(板の隙間は、ボールより広く、屋根の隙間は、ひもの太さより広く、ボール幅より狭いとする)。
結果的に山は3個となる。浮いた山は下の山を追い越し、循環する。
(4つの端点の内、2つは、山ぶら下げに興じ、残りの2つの端点は下の山を跨いだ背中こすりに興じている。)
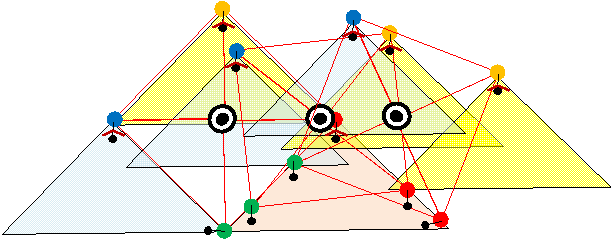
c. 観覧車の構造よりも複雑ですネ ?!
。
c. 上のサイクロイド曲線の釣鐘状の方が性質も良で、現実的カモ。丸い車輪も併用すると回転も同一。
c. 地面から見ると、この機械は3足歩行機(or 上を隠すと、2足歩行機)に見えるかも知れない。
c. 地面が少々凸凹や、坂、でも多分動作する。また、山の底辺を両端を残し削った形状(コンパス状)でも多分動作する。??
■ 車輪から見た山頂点の軌跡(制約特性)
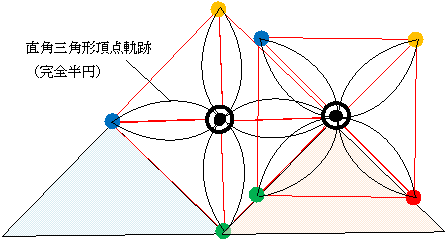
■ 座標軸すべり回転 (誰か作って下さい!)
(第4(又は第3)象限の長さ1の正方形の背中を軸の中心(0,0)を水平、点(0,-1)を真上にこすって90゜回転(こするモード)。
残りの3つの象限は背負ったまま回転(おんぶモード)。2つのモードの動的切り換え。)
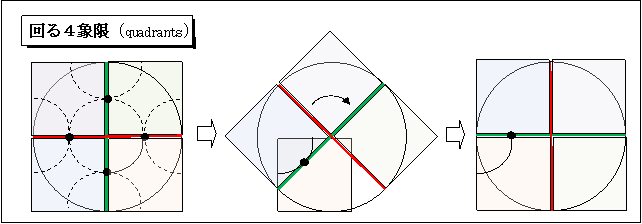
■ 仮想2倍径車輪(四角い車輪グループ)
(径2円内を径1の車輪が転がる車輪の模擬。)
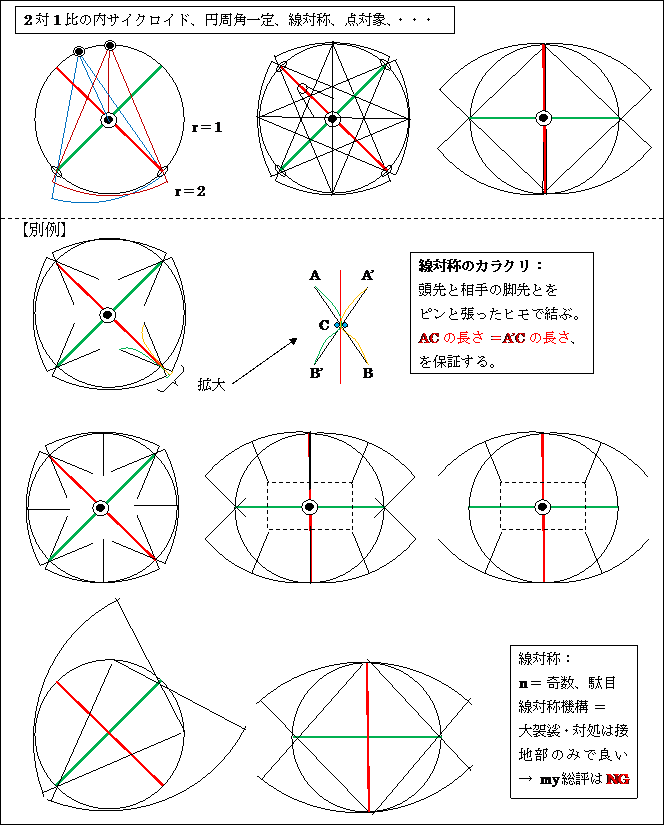
・ 非線対称の解の例(但し、誘導ナシのときは中央化配置機構が働くとする。)
(誘導壁とは、別名、手すり、である。)
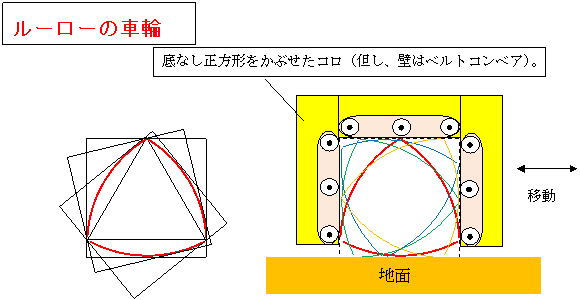
■ ルーローの多角形の車輪 を発案しました。
(ルーローの三角形は、機能的には、仮想2倍径車輪、に近い。)
cf. 特許公開例:ローラースケート用台座 by 秋山 仁 外1名、 公開番号= 特許公開2007-215820
-----------
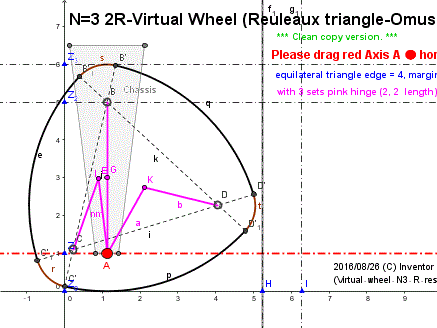
点 A ● が軸。
灰色逆台形は、キャスターのシャーシ/軸受け。
DEMO は、GeoGebra サイト
N=3 2R-Virtual Wheel (Reuleaux triangle-Omusubi)
この実装法は、ルーローの三角形車輪としては、
多分、世界一シンプルである。
--- チェックして下さい。
ルーローの四角形車輪 も容易。
N=4 Reuleaux concept Square Wheel
---------------
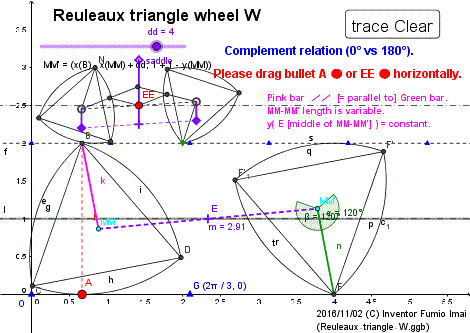
DEMO は、GeoGebra サイト
Reuleaux triangle wheel W
軸はブレても、車体はブレない。摩擦部は局所化されている。二輪駆動。
上下等幅の性質を、上接点を下接点に mapping して、軸の高さの平均 = 一定、を前面化、したもの。
両輪の接地点速度は v(≠ 0) と 0 を代わり番こ。しかし、 E の速度 = 0.5 v
▲応用: この車輪は、キャタピラの無いトラクタや戦車に成り得る。
---------------
■ ルーローの三角形の車輪の軸受けと軸 の案
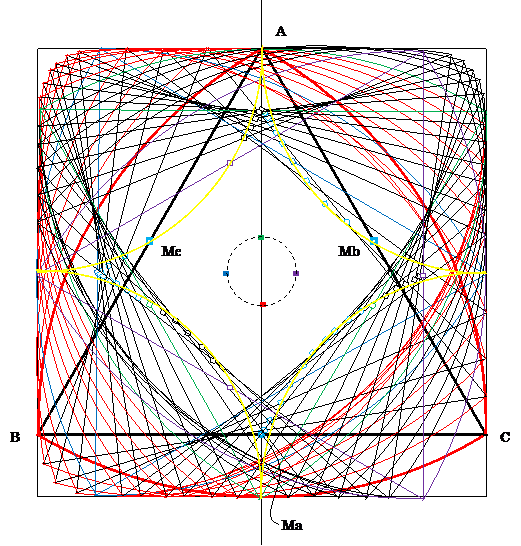
上図は正方形の中をルーローの三角形が接しながら回転するときの正三角形 ABC の各辺の中点の Ma, Mb, Mc の軌跡である。 ---- この図は、正方形内をルーローの三角形を壁面を強引スリップさせながら回転させたものである。
【定義】
正方形、正三角形の辺の長さ = 1
正三角形の高さ = √3/2 = 0.866..
コーナー = 正方形4隅から1-√3/2 の長さ以内の領域
□マーク = 正三角形の辺の中点の軌跡
黄色 = 4隅からの半円
■マーク = 正三角形の重心の軌跡(公転疑似円)
【特性】
① 3つの頂点A,B,C の3点は、通常2点が正方形の辺上に点接地する。残りの1点はコーナー内に位置し辺上に無い。
(1点が正方形の辺の中点で、残りの2点が丁度コーナーの境界にいるときは、3点とも一瞬だけ辺上にある。これは過度状態である。)
(正方形の4辺には、隣接2辺が正三角形の頂点による点接地、残りの(隣接)2辺【この2辺で挟まれた正方形コーナーには正三角形の点接地していない頂点が在る。】 には正三角形の前記点接地頂点の対辺を弦とする半径1の円弧による曲面接地【円弧が転がると対向頂点は地面と平行移動】、の接地状態が成立している。)
(上図の太線の正三角形をニラメッコして、少し移動したときの変化を想像して下さい。)
② ①の正方形の辺上にある正三角形の2頂点の中点は 0.5の半径の弧を描く。
(∵ 一定長の線分の両端が各々x軸, y軸上を移動すると線分の中点はxy座標軸の中心を中心とした円弧を描く。)
③ ①の正方形の辺上にある正三角形の2つの頂点は対辺に付いた円弧(半径1)が、正方形の辺の上を転がっている最中である。
対辺(= 弦)の中点はトロコイド曲線の軌跡を描く。
但し、正方形内の円の転がりはスリップしており、トロコイドは進行方向に関し縮小している。と私には思われる?。
④ 正三角形の中点の軌跡は下図の赤と青の太線の様になる。赤のトロコイドと青の半円との混在の図形である。
→ この太線の枠をルーローの三角形の正三角形の3の中点の位置を規制する制約とすると、3点は常にこの枠上をこする形となる。
(図中の小さい正三角形の各頂点は常に枠上をこすっている。)
→ この枠はルーローの車輪の軸受け、小さい正三角形は軸、として使える!?。
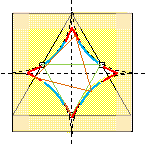
小さい正三角形のヘリを設定した場合、ヘリは壁と交わるときがある。
従って、もし小さい正三角形を軸にするなら凹なヘリにし、枠の壁と交わらない様にすべき。
■ 正三角形凸凹道 と 正三角形車輪 【藤原・掛谷の二角形、の変化】
(凸凹山の頂点は少しカット要) cf. ルーローの二角形, cf. 中心の軌跡 (3箇の楕円弧)
cf. 藤原松三郎, 掛谷(かけや)宗一
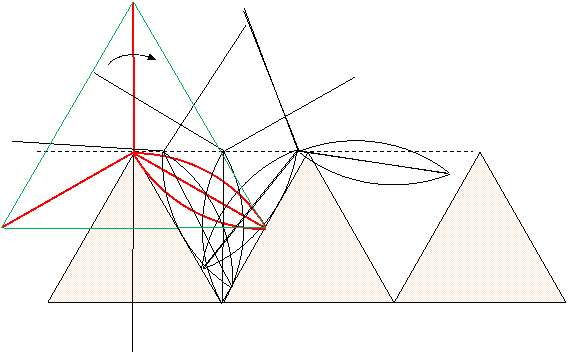
変化:半分化例(6角形)
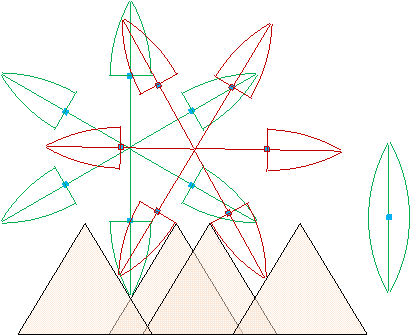
応用:三本足車輪(逆正三角形3つ)
→ これ、シンプルで非常に良い。 by ©鳩摩羅童子 on 2011/11/07
(誰か、この荷車作って。またデモ用自転車作って。) --- 難点は摩擦(運動不足の人用?!)。
(これにより、藤原・掛谷の二角形(ルーローの二角形でもほぼ可)の名を世界に広めて頂戴!!)
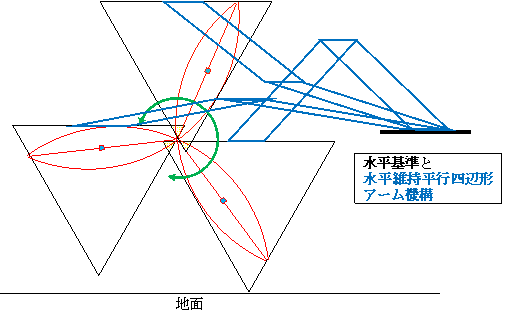
cf. 藤原・掛谷の二角形の応用 (人工心臓だって)
拡張応用:二本足車輪(下半円2つ) (上記応用の考え方を踏襲した変化)
(上図の平行四辺形アーム機構が3個あると軸と物理的にぶつかり実現難?。2個の解にする必要あり。
そうすると同じアナロジーではこの解となる。
・上の図と形も似ている。逆正三角形→逆半円(膨張した三角形)、レンズ→円(膨張したレンズ)。
・小円の位置を規制する大円中心と小円中心をつなぐ公転回転用アームを持つ。
・小円の一方の直径端の垂直方向移動に関し、大半円外へのはみ出しを禁止する。
つまり、大円中心水平面を天井とする規制を設ける。(∵ 追い越しの足引きずりを避けるため。)
追い越し機構は、結果的には大円中心をつかんで持ち上げるぶら下げ機構となる。
追い越し軌跡は、外側から見ると上半円を等倍横長化した半楕円弧。)
[暗黙使用特性:円の中に1/2の半径の小円を内接して転がすと、そのサイクロイド軌跡は直線(直径)]
(この動作は後述するチェビシェフリンク機構と少し似ている所がある。また、起き上がりこぼし的。小法師。)
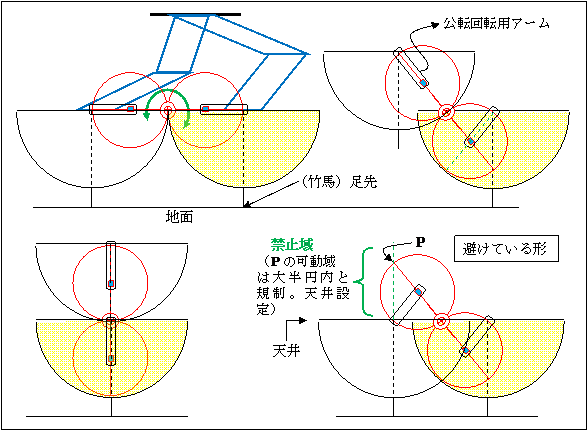
【変化2 車輪】 (60度の三角形は特異点的) cf. デルトイドの幾何学(その7)
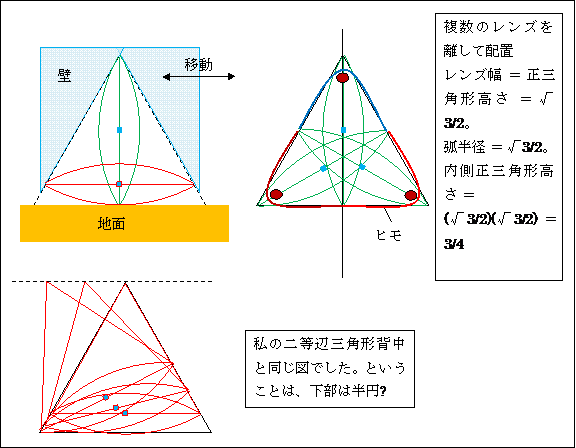
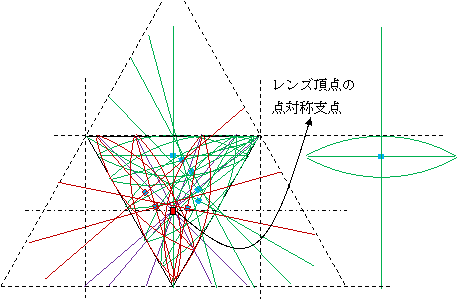
【変化3 車輪】 (レンズ1枚、逆さ正三角形、レンズ弧から中心への半径棒、レンズ頂点軌跡点対称棒)
【スリップしたサイクロイド曲線 の図】 Slipped cycloid
・「藤原・掛谷の二角形」の正三角形は、
サイクロイド曲線の線形化矯正・強制スリップ図とも云える。
(ルーローの三角形の正方形の方は、チーズケーキの円弧転がり時、中心(頂点)軌跡は地面と水平、
さらにそれをスリップさせても水平、の性質。)
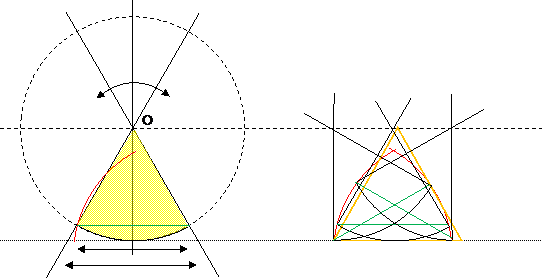
60゜円弧長 = pi/3 = 3.14159/3 = 1.047
大正三角形底辺長= 1/[sqr(3)/2] = 2/1.73205 = 1.154
赤 = サイクロイド曲線 (黄色はチーズケーキ円弧 (sector))
黄銅色 = スリップさせたサイクロイド
緑 = 弦
(左側赤曲線上にある緑弦の左端を水平にトントンとその右の左側黄銅色直線上にズラすと、
弦右端も右側黄銅色直線上に乗る。--- 面白いですね。)
★ 関連知識
① ルーローの多角形, 定幅図形, 自転車における幾何学の応用, フランツ・ルーロー,
n角の穴をあけるドリル(その49), wonderfl の Flash 図形, ルーローの2n(偶数)角形
② ひらめき☆ときめき サイエンス
③ サイクロイド・内サイクロイド
■ 「二等辺三角形の角に関する問題」 全然関係ない(「二等辺三角形」で Google したらありました。)
→ この問題は角だけで攻めても解けません。辺の長さの情報も必要です。高校数学の正弦定理を使うと誰でも解けます。
sin(x)/sin(40゜) = sin(x+20゜)/sin(80゜) の解です。 ()
i.e. tan(x) = sin(20゜)/[2cos(40゜)-cos(20゜)] --- = 1/sqrt(3) の数値 → x = 30゜
【 分母= 2cos(40)-cos(20) = 2sin(50)-cos(20) = 2sin(30+20)-cos(20) =
2(sin(30)cos(20)+cos(30)sin(20))-cos(20)=
2*0.5*cos(20)+2*(sqrt(3)/2)*sin(20)-cos(20)=sqrt(3)*sin(20)。
よって、tan(x) = 1/sqrt(3)。 x=30を目指したやっつけ誘導 】
【 別検証:x = 30゜とすると、sin(30)sin(80) = sin(50)sin(40) を検証すればよい。
左辺 = sin(30)sin(80) = 0.5*sin(2*40) = 0.5*2cos(40)sin(40) = cos(40)sin(40)、
右辺=sin(50)sin(40) = sin(90-40)sin(40) = cos(40)sin(40)、よって、左辺=右辺。 】
cf. 参1, 参2, 参3 ,,, c. sin(2x)=2cos(x)sin(x) の2倍角公式は、中心角は2倍の円周角、と等価。
2015/12/11 見たら、式の意味が導けない。忘れてしまった。もう一回やり直す。
∠ABC=80°, ∠BCD=50°,so, ∠BDC=50°,so, BC=BD, △BDEで正弦定理適用すると、BD/BE=sin(x)/sin(π-x-20°)=sin(x)/sin(x+20°), △BCEに正弦定理適用すると、BC/BE=sin(40°)/sin(80°),すると BC=BD なので、DB/BEとBC/BEは同一。つまり、sin(x)/sin(x+20°)=sin(40°)/sin(80°) ---- これが最初の式。
sin(x+20)=sin(x)cos20+cos(x)sin20, sin80=sin(2*40)=2sin40cos40, so, sin40/sin80=sin40/(2sin40cos40)=1/(2cos40)
i.e. sin(x)/sin(x+20°)=sin(40°)/sin(80°) は、sin(x)/sin(x+20°)=1/(2cos40), so, sin(x)=[sin(x)cos20+cos(x)sin20]/(2cos40), so, cos(x) で割ると、tan=[tancos20+sin20]/(2cos40), so, (2cos40-cos20)tan=sin20, so, tan(x)=sin20/(2cos40-cos20)。
これが2番目の式。
だって。
------
or, sin(x)/sin(x+20°)=sin(40°)/sin(80°)=sin(40°)/2sin(40°)cos(40°)=0.5/cos(40°)
0.5 は、sin(30°), cos(40°)=sin(90°-40°)=sin(50°) なので、
sin(x)/sin(x+20°)=sin(30°)/sin(50°) --- この式は、全て sin 。 x=30, x+20=50を満たす x は、x= 30 そのもの。sin(x) は、[0°,90°]区間で、単調増加一価関数なので、sin(x)=sin(30°) の mapping は、x=30° 以外には無い。また、差が20° の sin(x+20)/sin(x) が sin(50°)/sin(30°)=0.766044/0.5 になる点は、sin(x+20)/sin(x) は、単調減少一価関数なので x=30° 以外に無い。[Excel で確認した。]
★ チェビシェフリンク機構, 2, 3, Chebyshev linkage, 4, 5, 6 (Simulation of four-bar linkages),
Hoekens linkage (The Hoekens linkage is a Cognate linkage of the Chebyshev linkage.), Cognate linkages,
Roberts-Chebyshev Theorem, チェビシェフのリンク(ロボコン) (等価の図証明アリ※:
i.e. B'はBD中点、△BADでAB//A'B' and 長さは常に半分で一定 and A固定なのでA'も固定。
さらに、この図はB'C'の中点を支点にして上下点対称となっている。(B'とC', PとD, CとE 各々対応)
するとC'からB'A'に平行で同じ長さの位置は、A'に対応し、Pと水平で、DA'の長さの一定距離にある。)
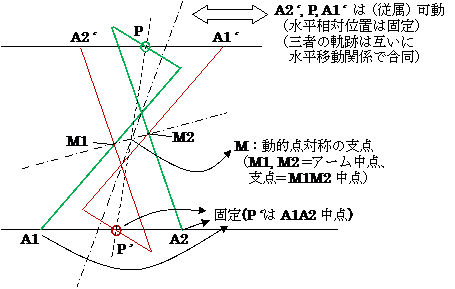
※:↑上の解説は余りエレガントでない(創造性を湧き立てさせない)。改めて私の直感を下図に示す。
(尚下図で、P の高さは両アームの高さの平均。A1‘ の高さは、1/2の両アームの高さの和、
A2‘ も同様。従って、点A2‘, P, A1‘ は同一水平線上に位置する。
また、P の x座標はベクトル表現すると、[(A1+2A1M1)+(A2+2A2M2)]/2 = (A1+A2)/2 +(A1M1+A2M2)、
つまり、線分A1A2の中点(A1+A2)/2からベクトル(A1M1+A2M2)位置にある。
A2'もA1からベクトル(A1M1+M1A2') = (A1M1+A2M2)と同一移動位置にある。A1'位置も同様。
つまり、点P はA2'A1'の中点。結果的に P' はA1A2 中点。
P が両アームの先端同士の中間(= 平均)というカラクリが効いていますネ。)
【チェビシェフリンクとホーキンスリンクとの間の隠れた点対称性】
【Hoekens Approximate Straight Line Linkage の図】(モーターは半径2の円)
別名 Chebyshev's linkage - alternative form と言う。 Hoekens ホーキンス

★ チェビシェフリンク二足歩行(点対称、平行移動変換) add on 2013/01/14

チェビシェフリンクとホーキンスリンクの軌跡に
点対称のリンク機構をかますと、左図の如く
二足歩行の脚の軌跡となる。
点対称 or 線対称 or 平行移動をかましてないロボットが
有るようだが(強度の問題?)、賢くない、のでは。 (1対nの比率の点対称も容易。)
cf. “からくり”のこころ (© 研究ノート: 関東職業能力開発大学校付属千葉職業能力開発短期大学校 平塚 剛一)
の「図4 チェビシェフ&平行リンク機構」に「1対n の比率の点対称」の機構あり。
■ チェビシェフリンク車輪 --- ここは、範囲名 "Cheby_wheel" です。
(チェビシェフリンク機構を原理とする車輪を以後「チェビシェフリンク車輪 (Chebyshev linkage wheel)」と呼ぶ。棒だけの車輪だ。)
【Chebyshev linkage 模擬の車輪への my拡張】 by ©鳩摩羅童子 on 2011/10/31
(脚型の車輪。三角形の車輪。これでも直線近似度はかなり高い。Chebyshev linkage を loop 化したもの)
(「右端=次の左端」との着眼。 5:4:3 の比率を 2:√3:1 へ変更した。この荷車を作れ。)
(1区間、赤: 0゜→180゜、赤から見た黒: 120゜→0゜、赤から見た茶色: 0゜→120゜。 歩幅√3の確保が難カモ?!。)
(もし赤の中点の軌跡が真の直線だとすると、これは赤の線分を直径とする円の転がりだと思う。
とすると、直径の両端の軌跡はサイクロイドである。つまり、『チェビシェフリンクの疑似直線とは、
円弧によるサイクロイドの近似である』 といえる。 厳密には、スリップしたサイクロイドも含む。
--- この認識はこの機構の神秘性を少し失わせるカモ??。)
(下の図を見ていると、サイクロイドの法線の包絡線はサイクロイド、サイクロイドの伸開線はサイクロイド
の図、のパクリにも見えてきました。 ex. 長さ2のアーム(=半径)の回転が、伸開線の糸が開閉する様子、に見えませんか?。)
cf. サイクロイドの性質(接線角)
(赤線分の回転の動き(半径 0.5)は、まるで競歩のオッチャンの腰使いの様にも見えますダ。黒と茶色は左右の脚。
そして、腰の重心がブレていないスゴイ歩き?!カモ。)
(良く分かりませんが、黒と茶色の交点は、赤の中点のほぼ真下にありますね。 why???。
しかも、私の比率の場合、交点の高さはほぼ 1 で一定。 why???。 5:4:3 も同傾向。)
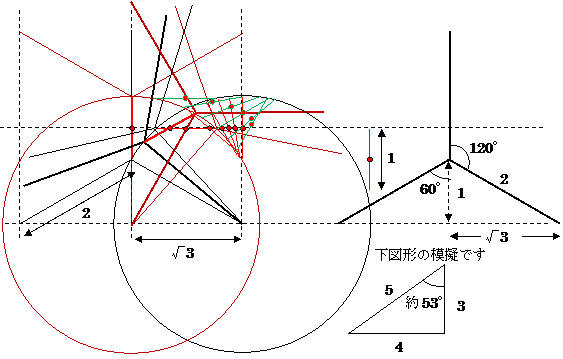
赤の中点の高さは、
端の時、 1.5
√3 の真ん中の時、√(3-(1/2)*√3) = 1.460813
gap = 0.039187008
gap/1.5 = 2.6125%
足先に四角い 車輪 ■ を付けると足元が滑らなくて良いかも。
【Tchebycheff's Engineers' Table】 Another bit of excess - but a valid, real-life application.
http://www.mfdabbs.pwp.blueyonder.co.uk/Maths_Pages/SketchPad_Files/Mechanical_Linkages/Mechanical_Linkages.html
Below figure's Copyright is in above site all. ©Mark's Maths and Excel Homepage

c. 左図は非常に魅力的である。
チェビシェフリンク + ホーキンスリンクの一ひねりしたもの、である。
c. 上図に、赤中点の左右(歩幅√3)÷2 に長さ1 (= 脚長2÷2)
のアームを追加し脚の中点に繋ぐ。
可能?! → yes! (but 区間またがりの連続性に少々難あり)
(アームは結果的に他方の脚と平行)
(追加アームと脚両端は直角三角形と2つの二等辺三角形、形成。
つまり、脚を直径とする半円と水平線との交点。)
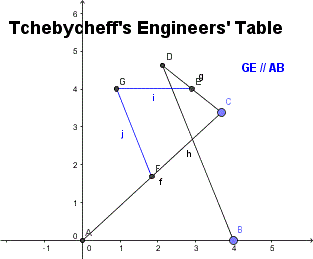
【5:4:3 比の威力】

cf. CHEBYSHEV LINKAGE --- c. 外人さんは、5:4:3 の直角三角形と気が付いていない様ですね。
(蛇足:この記事の The Linkage の解説の前半部分は BとD が逆になっていて図と喰い違っている。編集レビューされていませんね。)
変化 (地面中間に第3の脚を付け、90゜(180゜中間)回転角度の所とつなぐ。OKか?)
→ ≒OK !。 第4、第5・・の脚も多分可能(比例位置・比例角度)。∵回転円の近似度が非常に高いから。
(発想的には、この図は単に半区間遅れた図と合成しただけである。90゜位相ずらし。従って正しい。)
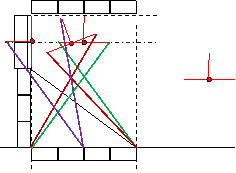
【チェビシェフリンク車輪 第2の案】--- 脚型キャスターの方式としては最も simple。
(©鳩摩羅童子 on 2011/11/11 @0:11 縁起のいい日?。
改めて記しますが、下記考案の知的権利は全て鳩摩羅童子に帰属します。 死後50年まで、著作権による保護。)
前述した「拡張応用:二本足車輪(下半円2つ)」の図を見ていると、
チェビシェフリンクの動作図とよく似ていることが分かる。半大円の中で1/2の大きさの小円が180゜回転すると
水平軌跡一区間が生成される。これはチェビシェフリンクの中間線分が180゜回転すると
その線分の中点により疑似水平の軌跡の一区間が生成されるのとそっくりである。
区間またがりの機構も真似すると、アナロジーとして下図の「その1」「その2」が思い付く。
2本の脚のアームに対する追い越し用アームを用意する。
その1は、赤回転線分に関して線対称に配置する。
(この図は、【Chebyshev linkage 模擬の車輪への my拡張】の第1の案の変化とも看做せるが、
脚が3本3本から2本2本に減ったが、線対称機構を追加しなければならない。優劣付け難い?。
尚、A'B'の距離は一定。で自由度を1つ減らせる。→ 案1より良い。また、他のいづれの今までの私の車輪より良い。)
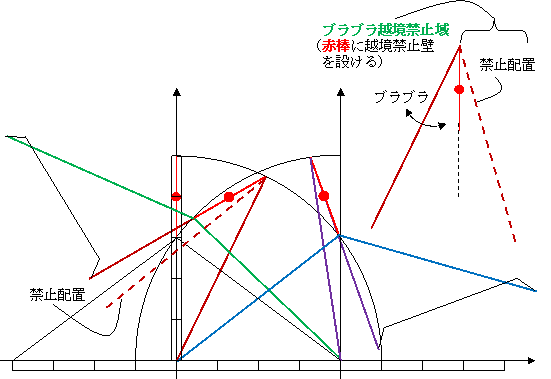
■「その0」
その1は、赤回転線分に関して線対称に配置する。 の模擬は実は簡単でした。追加バー1本で可能。
cf. Chebyshev N=2 Polygon Wheel (GeoGebra) on 2016/07 ---- 99% 線対称を実現しています。
下の、「その1」、「その2」、は、現時点では既にゴミです。(しかし、昔は下記が最善だと思っていたのです。)
■「その1」
Chebyshev linkage wheel
 ∠ は、約 45° より小さくなったら、0° と予測して良い。
∠ は、約 45° より小さくなったら、0° と予測して良い。
c. my 印象:この車輪の荷車は、脚の長さをある程度とると、階段の段差なんてみんな引っ掛けて、屁のカッパ ??。
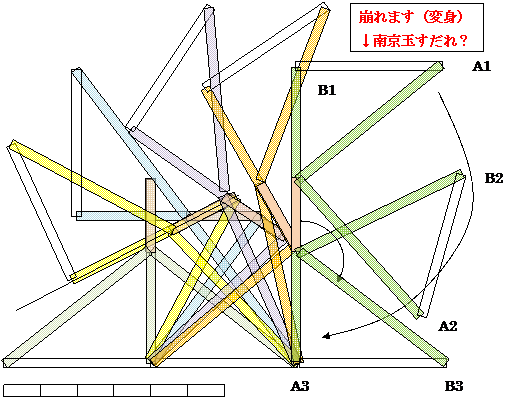
■「その2」
追い越し用脚を用意し、赤回転線分に関して反対側に行かない様に規制する。(∵ 追い越し未完回避)
追い越しの図形はぶら下がりの形に近く、重力に従って変形(途中でバタッと崩れる?)する。
(こちらの方式では線対称機構不要。足先間の長さ4の距離確保のアーム相当要。階段対応微妙。)
→ コレ simple で良い。棒と蝶つがい(蝶番, hinge)だけで出来る。また、パタンが非常に良い。
cf. 車輪 (wikipedia ※), 車輪 の画像検索結果 (by Google)
※: この 車輪の wikipedia 記事に私の上記 「チェビシェフリンク車輪」 も記載して欲しいものだ。
また、誰か、私のこの考案が世界初であることを検証・証明して下さい。
(当方連絡先 E-mail: imai-imaiあっとまーくmri.biglobe.ne.jp [あっとまーく、は英一文字に直して下さい。spam 対策表記。] )
荷車のイメージ図
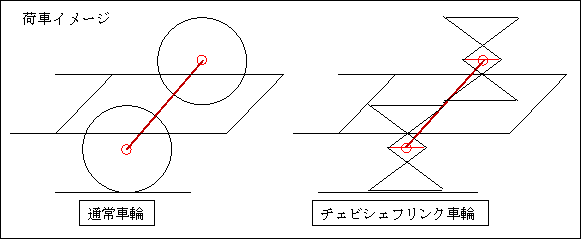
c. もし私がチェビシェフさん自身だったら、容易にこの車輪の構想まで思い付くと思うが、
何故無いのだろうか。有ったのだが何か問題が有って黙っていたのだろうか。
--- 誰か、究明して下さい。
cf. 参考: Chebyshev's Four Bar Linkage (flickr from YAHOO! USA) --- PR コメントを投稿しておきました。on 2011/11/13
cf. 工作サンプル (image, movie) --- アームの形にぶつからない工夫アリ。
c. 英単語 wheel (車輪)の語源について: 語源は、コロ (kolo) [wh は h に音通。 h は k に音通。l-l]。 → コレ半常識?
■ ロバーツリンク (Roberts linkage)(2点間直線往復),,,, 1
この運動は、直線スライド運動のスライド部を置換し、スライド方式の摩擦を軽減できると思う。
この疑似直線のためのリンク長の比率は甘くて良いらしい。 cf. Roberts'curve linkage
【ロバーツリンクの my 不可解】 (下図のどこかオカシイ?)
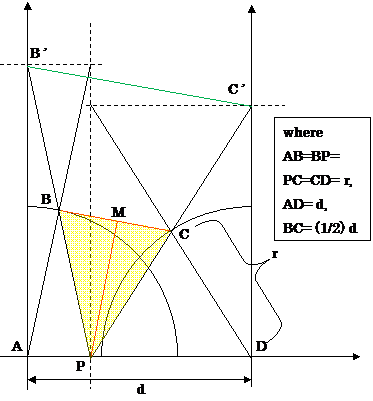
左図はロバーツリンクの図である。
また、BB'=CC'= r で 点BはPB'中点、点CはPC'中点とする。
もし、点PがAD上(x軸:横軸)をスライドするとすると、
点B', C'は y軸(縦軸)上をスライドする。
(↑この話は有名な話だ。
i.e. 線分の両端を x軸と y軸の上に置き、こすると、その中点の軌跡は円弧。)
また、△PB'C'は△PBCの2倍の相似形。
つまり、B'C'はBCと平行で、長さ2倍。B'C'= d。
B'C'= d だって、冗談でしょ??!!。
(B'C'は水平で無いのに、長さは水平のものと同じ、だって!!!!)
どうしてこうなるのか、私には合点が行かない。
→ 多分 点P は 線分AD 上に無い。もっと下方にあり、
B'はもっと右&下方、C'はもっと左&下方にあるのだと思う。
(点P は山の形の軌跡、AD中点の山の頂上のみAD直線上に位置する。)
→ 本来なら、Bを通る垂直線とCを通る垂直線との水平距離[=幅]= (1/2) d 、と規制すべきである。
失敗作【ロバーツリンクの my 改造】 (厳密な直線軌跡) --- 解釈ミスあり。しかし、記念に残す。
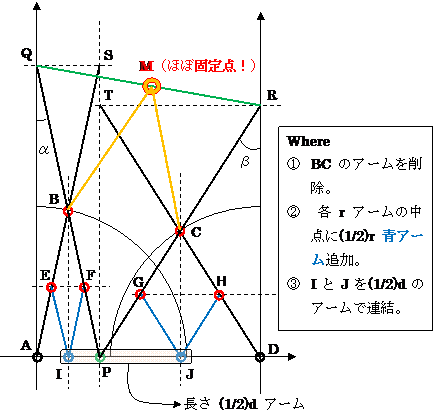
左図はロバーツリンクの改良である。
疑似直線ではなく正確直線を生成する。
この解は、アーム数が多過ぎますね。
自分の中に自分の(1/2)のコピーを含んでいる。 recursive (再帰的)構造。
点P, I, J, Q, R は皆、直線軌跡を描く。
↑ IJ=(1/2)d は、恒等式であり、(1/2)dアームを連結しても、無いのと同じ。つまりこの解はウソ(設計ミス)。
(I が AP中点、J が PD中点、なら、
P がどこにあっても、IJ=(1/2)d が成立。)
---- BI // CJ (平行)を規制する機構があればいいが、菱形のクロス線の方向を同定する棒が無い(スライドになってしまう)。正規化方向子(長さ 1)機構って無いのか? --- 誰か教えて!。
(「3点A, P, D が一直線上にある。」 ←等価→ 「AP の垂直2等分線と PD の垂直2等分線と、が平行。」 ←等価→ 「S, T, P が一直線上にある。」)
【補足】点Q と点R の中点M を考えると、M はADの垂直2等分線上を移動する。
移動範囲は狭く、ほぼ固定点に近い。しかし、どこかに固定し、さらに黄銅色のアームを付加した構造を試しに考えると、アーム全体も固定してしまいうまく行かない(規制が強過ぎて自由度をゼロにしてしまう)。 従って、M を固定する黄銅色のアームの解は無い。
→ もし、スライド機構を許すなら、点M を縦棒スライド化するのが良い。
■ ポースリエのリンク (Peaucellier linkage/ Peaucellier-Lipkin linkage) (厳密な直線軌跡),
ポースリエの機構の原理 (幾何証明アリ),
Inversive geometry c. Inversor 反転器って、誰が名前付けたの。 inverse/ inversion は「反~」では無く「逆~」じゃないの。逆変換器だんべ。
, 蒸気機関でピストンの往復運動を回転運動に変えるリンク機構 by ©坂田 明治
, マジックハンドなど面白動作の多節リンクたち (ブリカードの直線運動、ケンプの直線運動)Copyright(c) 2013 ITmedia,
---- 【No.48】平行定規(2)の解説まだ良くない。図も悪い。垂直に上下する訳がない。間違いだ。横に幾らでもズレる(どこへも移動可能)。もし、本当に垂直に上下していたら、直線器として名が残る。
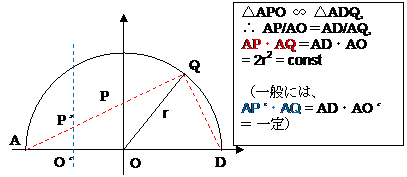
Inversive geometry:
左図は 円の内側に直線を引くケースの条件である。
(P, Q の関係を入替えた。)
A, O 固定。Q 円、P 直線。
直線は AO (固定した点同士をむすぶ線)と垂直。円は A を通る。
【参考】
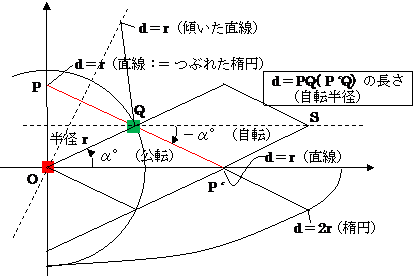
直線 → 円仲介 → 直線(or 楕円)の mapping の代表例。 逆も真なり。
(通常、線対称[= -α゜の等速逆回転]化は、スライドなしのリンク機構のみでは不可能。
ex. 左図で、点S を水平移動と規制するには、Q から水平棒をつなぎ、S にスライドを設け、棒をスライドに通す。
しかし、今だから言うが、Sの直線運動をポースリエのリンクで規制すればスライドは不要。しかし、大袈裟。)
d = r :直線
d ≠ r :楕円 (d = 0:円)
ポースリエのリンクは、
(点 →) 円 → 直線 の mapping 例である。 逆も真なり。
【楕円描画】 ellipse drawing 【線 → 線】
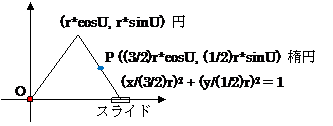
【参考】
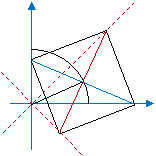
左図を見ていると、ポースリエのリンクの水平菱形つぶしの上半分の形がなんとなく想像される。
y = l cos(u) - m cos(v), x = l cos(u) + m cos(v), l sin(u) = m sin(v),
∴ xy = l2 cos2(u) - m2 cos2(v)
= l2 - m2 + [- (l*sin(u))2 + (m*sin(v))2] = l2 - m2
----この式の値が、x2/a2 - y2/b2 = 1(双曲線)に似ているのは偶然では無い。 ∵反比例曲線は(直交 [a=b])双曲線の45゜ズラシでもある。
(菱形が横ペッタンコの時:x= l+m, y= l-m, 菱形が縦ペッタンコ(最高高さ)の時:x=y=√(l2 - m2))
cf. 反転の作図法 (基本の作図) by ©私的数学塾 --- 反転器の形は、この幾何の作図法に似ているが少し異なる。面白い!。 コンパスのみの作図。
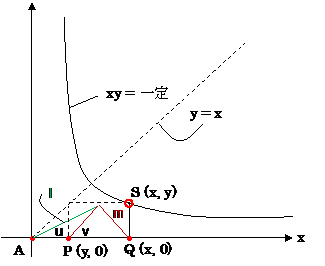
cf. 近世幾何学よりみた幾何指導内容について 「(四)極と極線について」 by ©出石, 隆, 1961-03-15, 高校教育研究, 12: 33-37(金沢大学)
【参考】 ポースリエの反転器と極点と極線の関係 --- by ©鳩摩羅童子 ここは、範囲名「Polar」です。
(これは、「水平菱形つぶし」の形の反転器の形が唐突に出来たものではないことの My 検証です。)
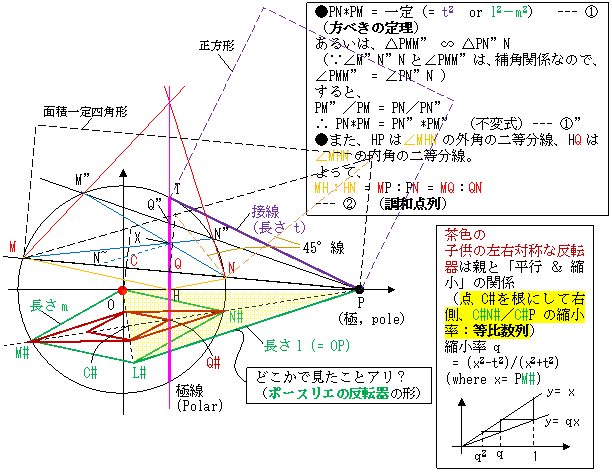
・ 点 C は弦 MN の中点。
誰かポースリエの反転器から極線を描画するリンク機構を考え出して下さい。
on 2012/01/15
→ たとえば、左図下半分の様にする。
→ 実現方法不明。その時点の親と相似な子供を作る必要アリ。アームは可変長。
・アームは右半分だけで可?。
・点C#はOC#⊥C#PなのでOPを直径とする円を描く。
・C#N# の長さは C#P のq 倍。C#Q# の長さは C#P のq2 倍。
cf. 「極と極線」 と 「調和点列」の話 --
-- 誤植アリ 、円C→ 円O,
a2=OP×OH だったので、PO2-a2=PO(PO-OH)=PO×PH ,,, 定理1と定理2 は関係あるの?。
cf. アポロニウスの円, 外角の二等分線
cf. Pole and polar, Inversive geometry, Pole and Polar with respect to a Triangle, How to draw an exact straight line! [Hart's linkage --- アーム数5だって。他にも沢山あるって。]
cf. Hart's Inversor, Poles and Polars (Polars の集合が極線?), Hart's Inversor (これ詳細)
cf. 方べきの定理, 「方べき」とはどのような意味なのでしょう... , 調和平均作図, 台形に潜むいろいろな平均
c. ∠MHQ = ∠NHQ の角度の±変換機構のスライド無しリンク機構は重要だと思う。アーム長が固定なら、直線描画なんてチョロイ。点 H 以外の極線上の任意点 Q では、この性質は保存されない様だ(?)。--- 良く分かりません、XQ が∠MXN を二等分、XQ" が∠M"XN" を二等分、なのかも知れない。誰か確認して下さい。
cf. ■ベルヌーイのレムニスケート(その4) -- 【2】ハートの反転器
リンク数は多くなると機械として実質的に動かなくなるので,リンク数の少ない単純な仕組みが望まれる.ポースリエの反転器が7リンクであるのに対して,1875年,ハートは5リンクから構成される直線運動メカニズムを構成した.これ以上(4本)リンク数を少なくすることはできない.
→ 「できない」って、証明出来るのでしょうか?。実は、私は4本の直線描画リンク機構を発見しましたが(下方に図アリ)。 by 鳩摩羅童子 on 2012/01/31
【上図の発展】 極線上の点が別の円の反転の条件を満たす、ことの発見。 by ©鳩摩羅童子 on 2012/01/22
(これは図のニラメッコの結果です。)
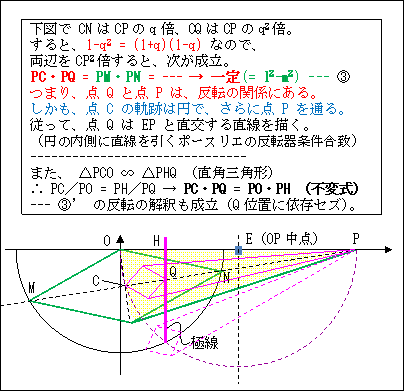
極線の比例数列(2乗比)の性質を用いた描画の新しいリンク機構は難しそうである。
その代わり、極線上の縮小比 q2 の点が直線を描くのは、この点が反転の性質を備えていることから説明出来た。
反転関係の円は、OP を直径とする円であり、円 O に対する双対の点 P を中心とする円とも異なる。
③の式は、まるでマジック?。
この式は、さらに PC = (PM+PN)/2 を使用すると、
PQ = 2(PM・PN)/(PM+PN)
i.e. 2/PQ = 1/PM + 1/PN --- ④ :調和平均の関係。
この式は入試問題に出るらしい。--- 少し異常ですネ!。
式③が正しいとすると、円 O に関し P からの割線 PNM に対応して、PQ QC の長さの割線が円 O に関して存在する (mapping) → 本当か?。この mapping はどの様な性質を持つか?(左図ピンク破線)
前の図で、青色のクロス直線の交点 X が極線上にあるのは偶然では無い。図形的にはこの点は、調和平均の交点である。
さらに、円の内側の方べきの定理から、M"X・NX = MX・N"X _= 一定、の「一定1」と PN・PM = PN"・PM"_= 一定、の「一定2」とは同じ一定値か? --- 一定1 = m2, 一定2 = l2 - m2 の関係。
△PMM" ∽ △PN"N, △MM"X ∽ △NN"X の相似比は MM": NN" で共通である。つまり、PN"/PM=PN/PM"=XN/XM=XN"/XM"=NN"/MM"= k PN"/PM=XN/XM は、図の上では、△MN"P ∽ △MXN~ (∵ ∠M"N"M = ∠M"NM 同一円周角, すると ∠MN"P = ∠MN~X [XN~ は XN~ = XN なる補助線])。これは②の調和点列の比に等しいが、限りなく M と M" を接近させても成立すると考えれば良い。つまり、方べきの定理の円の内点と外点の2つの式から、M, Q, N, P の調和点列性が導出される。
比 b/a = c/d のとき (a+b)/(a-b) = (c+d)/(c-d) ∵ (a±b)/a = (c±d)/d → (a±b)/(c±d) = a/d → (a+b)/(c+d) = (a-b)/(c-d) → (a±b)/(a∓ b)=(c±d)/(c∓ d) 【合除比の理】、なので、弦MN の中点を C とすると、PN/MP = QN/MQ → (MP+PN)/(MP-PN)=(MQ+QN)/(MQ-QN) → 2CP/2CM=2CN/2CQ → CP/CN=CN/CQ=1/q → CN=q・CP, CQ=q・CN=q・(q・CP)=q2・CP つまり、数式的にも弦の中点 C から見て、点 Q, N は等比数列だと証明される。
また、CP・CQ = CN2 --- ⑤ [PC・PQ では無い。C が起点。CN は弦の半分の長さで可変長(非一定)。C は半径 CN の円の中心とも考えられる。] も成立。⑤の式は、点Q とP が円 C に関し、反転ペア (an inversive pair) であることの定義式でもある。
■ 双対直交円
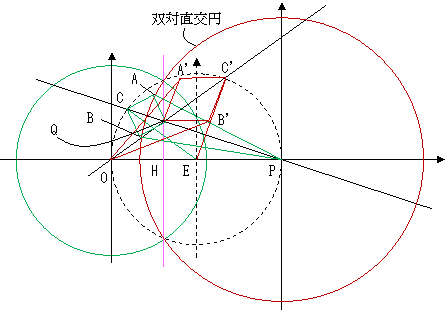
円 O と極 P の極線は、円 P と極 O の極線と共用である。
OP を直径とする媒介円(割線の弦の中点の軌跡:破線部)も共用。
【参考】 極線に対するポースリエの反転器と惑星の公転と自転の関係
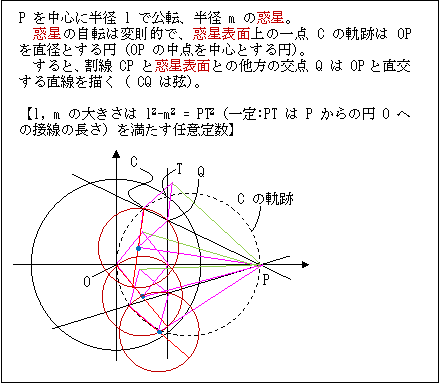
自転は等速で無い?。
l の長さを PT の接線の長さに設定すると、惑星の大きさ m はゼロ? → 意味不明 !!
【参考】 (ポースリエの反転器の見方・解釈の変化) --- また、半円の図ではない。
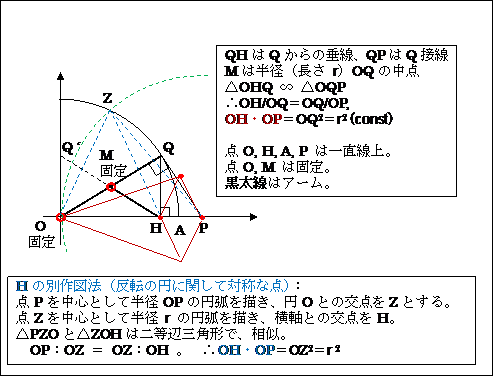 ① M を固定したと絶対的に見ると、H を M を中心に回転、すると P が Q の接線上を移動。
① M を固定したと絶対的に見ると、H を M を中心に回転、すると P が Q の接線上を移動。
つまり、H (円) → P (直線)
② 見方を変えて、H の方から相対的にみると、①の行為は、M (or Q) が回転、A は固定、
H, P は O と A を結ぶ水平直線上を移動。また、 Q' は垂直線上を移動。
つまり、Q or M(円) → H, P or Q'(直線)
反転器の水平菱形の左右両端は、垂線・接線交点に対応。
QP は Q の接線なので、Q が上に行くと P は∞の彼方。
(ってことは、垂線 H は O に到達出来ない。)
OH・OP = r2 の式は、実は反転器とは関係無い。一般式は、前述した ⑤ である。弦が直径のときの瞬間値であり。積の値は可変(非一定)である。
【ポースリエの反転器 から ハートの反転器 誘導】
これは feeling で書いています。私の直感が間違っているかも知れません。 検証して下さい。→ 間違っていますネ。
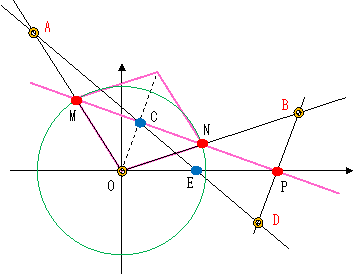
① OM 延長 ② E と C を結ぶ線を引く ③ ON 延長 ④ ON 上の適当な点 B と P を結ぶ線を引く。 ( E = OP の中点、 C = 弦 MN の中点)
クロス型菱形 AOBD (蝶々型、8の字型、ひねり四辺形)がハートの反転器?。
cf. b. 交差リンク機構 --- 左右対象なので、△をの足乗せれば、その頂点は垂直線を描く。直線描画なんて簡単?
ひんじを動かして変形しても、M, N, P の関係性は維持される。C, E の性質も維持。co-linear (一直線・共線)性も維持。
c. 「ひねり長方形」で無くても良いのかも?。 → 多分、NG。
ハートさんはスゴイ。
cf. ハート (Hart) の反転器 by ©坂田明治
★ 2015/12/5。 記念に残しておく。---- 何気なく書いているが、これを見つけるまでに、実は、ウン年掛かっている。
(実は、直線器描画の、斜めから腕が伸びる方式には、違和感がある。思考が、素直ではない。基準・単位線分の 2 点を固定し、そのママ伸びる、の方式も必ずある、と思っていた。やはり、あった。また、反転器は、積が一定であり、片方が伸びれば、他方は縮む。しかし、私が欲しかったのは、片方が伸びても、他方は、固定で縮まない反転器だったのです。実は、もう一つ欲しいのがある。それは半径 r の二等分線が、長さが r cos (θ/2) の垂直二等分線ではなく、長さ r の 真ん中の棒である。cos (θ/2) の長さの棒なんて要らない。長さ r の棒であるべきだ。)
反転器が3個あれば、2点間直線描画リンク機構は簡単に実現できる。13 bars.
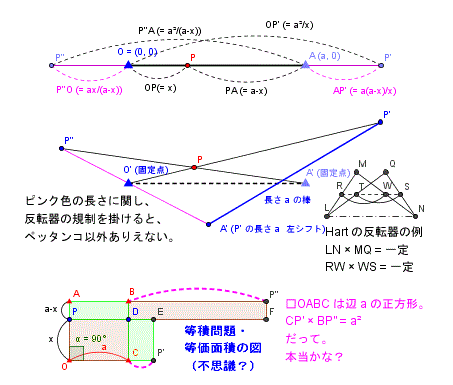 左図は、基準点 O (0, 0) と A (a, 0) の長さ a の線分の内分点 P を可変的に移動させるリンク機構があることを示す。
左図は、基準点 O (0, 0) と A (a, 0) の長さ a の線分の内分点 P を可変的に移動させるリンク機構があることを示す。
P' は P の左側OP (長さ x とする) に対する、反転点である、反転は、積が a2 一定とする。つまり、 x に対する反転長は、a2/x である。P'' は P の右側 PA (長さ a-x) に対する、反転点である。反転長は、a2/(a-x) である。
すると、なんという自然の摂理か、AP' = a2/x - a = a2/x - ax/x = a(a-x)/x, P''O = a2/(a-x) -a = a2/(a-x) -a(a-x)/(a-x) = ax/(a-x)、となっている。 つまり、2つの長さを掛け算すると、a2 である。つまり、反転器の規約そのままである。
【別解】cos2Θ + sin2Θ = 1 (和が一定), 1/cos2Θ - 1 = (1 - cos2Θ)/ cos2Θ= sin2Θ/cos2Θ= tan2Θ。 同様に、 1/sin2Θ - 1= cotan2Θ。なので、(逆数-1) 同士の積は、(tan × cotan)2= 1 (積が一定)。恒等式である。
これを逆手に取り、AP', P''O の長さを反転器配下に管理させると、点 P は 線分 OA の上をズレることが出来ない様に規制される。【 Geogebra でも確認した。正しい。】
AP' は、左へ a シフトし、積の2つの長さを背中合わせに配置する反転器を適用する(点 O [or 2番目の図の 点 O'] を起点の反転器。 i.e. P''O'A' の Pink 色線分の反転器)。
---- 2番目の図のリンク機構(点 ▲ O' (固定点) がある図)には、線分 O'PP' に反転器適用、線分 A'PP'' に反転器適用、線分 P''O'A' に反転器適用。つまり、計3セットの反転器適用。
この図において、A'P' の青棒が無いとすると、点 ● P が O'A' 上に無いと、A'P' の距離は、常に a より大きい。 P が O'A' 線上にあるときだけ、 A'P' の長さは just a である。だから、固定長 a の棒を A'P' にかますと、点 P の位置は規制され、線分 O'A' 上の移動のみ許される。
関係点は、最初から全て一次元上の世界である。反転器の装置が実装的に2次元にたまたまなっているだけだ。
つまり、リンク機構の全体のリンク数は、4 本の反転器が 3 セットと、AP' を左にズラス 長さ a の棒 1 本、の計 13 本である。
なお、P は、外分点化も可能である。
本方式は、web で調べたが、今まで提唱されていない。回転 → 直線、ではなく、直線 → 直線の方式である。内分点でサポートされている従来リンク機構は、固定比例点、中点であり、可変の内分点は実現されていない。しかし、反転器を利用すれば、可変内分点機構が実現できるのです。
Hart's の A-frame を利用する従来方式では、5本で底辺上の直線描画ができるので、リンク本数の観点から見ると、完全に負けている。しかし、機構が垂直方向の直線描画を介さないので、総合的には優劣は付け難い。装置の面積の大きさは、多分優秀で、コンパクト。案外良い方式かもしれない。少なくとも、回転を介す斜め方向からの実装ではなく、思考が素直である。
下に、従来方式の内分点の図法を示したが、2次元平面での作図である(固定点は、両端と、点 O は、一次元上で無い。M は、一次元上。)。バーの本数は、5本で可能。しかし、上記方式は、一次元世界の作図である(固定点は、両端の2個のみで、一次元の世界。)。次元を上げると、本数は減る。当たり前の世界だ。3次元装置だと二次元上の直線は、バーは4本で可能である。直角三角形(2本のバー、2a の棒と、中点から a の棒の例のフレーム)を2組、3つのノードの内各2つ同士はつなぎ、Z 軸方向にし、立体に組み、同じ可変長高さにする。xy 平面には2等辺三角形ができる。共通 Z 軸の足が、2等辺三角形の頂点となる。z 軸方向の高さを変えると、2等辺三角形の2辺の長さが変わる。2等辺三角形の底辺の両端を固定し、直角三角形の z 軸の高さを変えると、2等辺三角形の頂点が直線を描く。
つまり、直線描画は、3次元だと4本、2次元だと、5本、1次元だと、13本となる。のかもしれない。
cf. 自然の摂理という意味で、feeling 的には、「チェバの定理 (Ceva's theorem)」 と少し似ている。
cf. 平面図形 | 高校数学の美しい物語, or 調和点列の様々な定義と具体例 --- 似ているけど、違うね。
■■教育的 お遊び■■ --- これは、数式的には恒等式である。等積問題と和が一定、の場合の摂理。4変数の足し算と掛け算。
男1 + 男2 = a ---- 式 ①
男1*女1 = a2 ---- 式 ②
男2*女2 = a2 ---- 式 ③
もし、① and ② and ③ ならば、次が成立。
(女1- a)*(女2 - a) = a2 ---- 式 ④
逆に、② and ③ and ④ ならば、① が成立。
補足:
ハ-ト (Hart) のインバーサー (inversor) は、平行移動の▱ 平行四辺形のリンク機構を対角線に関して、2辺をひっくり返した、図形である ( Antiparallelogram )。外見は左右対称の台形である、下底 LN と上底 MQ の長さは、片方を伸ばすと、他方は縮む。実は、その長さの積は常に一定である ( LN × MQ = 一定 [実は、元の平行四辺形の2辺の長さを a, b とすると、積の値は、a2 - b2, , a = b だと正方形で、台形は三角形に縮退してしまい、積はゼロ。] )。つまり、等積問題のツールになる。しかし、下底と上底は平行だが、一直線上に無い。しかし、下底の一定倍、と、上底の他の一定倍、の長さを持つ長さが、一直線上に並ぶ点が装置内にウジャウジャ存在する。それは、底辺/下底と平行な線と、棒との交点の点列 R,T,W,S である。
例えば、高さの下から 1/3 の所に平行線を引くと、RW = (2/3) LN, WS = (1/3) MQ であり、RW*WS = (2/3)*(1/3)*LN*MQ = 一定である。
また、 RT = WS で同じ長さなので、RW*WS の積(W から見て2つの長さは背中合わせ)、は、ST*SW の積(S から見て 2つの長さは同一方向)と同じ。
実は、平行線は、高さを下底より下に引くこともできる。ML の棒を L からも延長すれば良い (QL, MN, QN の棒も延長する)。つまり、平行線は、高さの内分以外に外分点にも引ける。
外分したインバーサーの方(腕長の植木バサミの形に似ている)が、装置がゴチャゴチャしていないので、私は好きです。
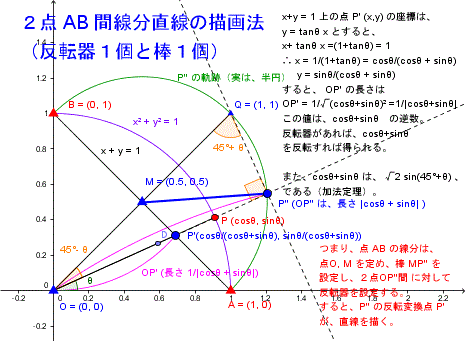 2点間線分のオーソドックスな描画法は、左図である。
2点間線分のオーソドックスな描画法は、左図である。
2点が定まったら、中点 M と、M の真上の高さ 0.5 線分の所に起点 O を定める。
点 M を頂点とする長さ 0.5 線部の棒のブランコを定める。
ブランコの椅子 P'' と起点 O の間を反転器でつなぐ。
ブランコを揺らす。
P'' に対する反転の点 P'(OP' の長さは OP'' の長さの逆数)は、2点を結ぶ直線を描く。
--- よく見ると、線分は、円の直径部で、点 O は、その直径に対する円の頂点で、M は、円の中心で、MP'' は半径で、点 P''は下半円上の点で、これをブラブラさせると、距離 OP'' の長さは、変わる。起点 O から OP'' の長さの逆数の短い長さの点を P' とすると、P' は直線を描く。
つまり、下半分の半円軌跡が反転で、直経の直線に射影される。
面白くも何とも無い (?)。
【 式の世界で cosθ+ sinθ の長さの可変長半径の軌跡が、半円になること。その逆数の 1/(cosθ+sinθ)の長さの可変長半径の軌跡が直線 x + y = 1 になる、事の方が面白かった。 cos45°= sin45°=1/√2、で、sin(α+β) = sinα cosβ + cosα sinβが、sinα + cosα に化けるトリックの方が面白かった(βの 45°指定。詐欺師ですね)。言われなければ、多分、想像できない。】
【二足歩行器の制御のヒント:ホーキンスリンク+ポースリエのリンク】
ポースリエのリンクの円弧入力部をホーキンスリンクの逆さカマボコの比率を変えた、あるいは、ホーキンスリンクの軌跡と円弧との合成により、逆さ(お椀型)三日月の形とし、脚の一サイクルを作る。 → 誰か try して下さい。
cf. リンク機構5(ショベルカー)(YouTube)
---- 近いのを偶然見つけました。 ショベルの中の点の軌跡(但し、これは両方とも円で無いかもしれない?)
■ ポースリエのリンク車輪 --- ここは、範囲名 "P_wheel" です。
(ボースリエのリンクの直線引き機構の原理を用いた脚型車輪。 Peaucellier Linkage Wheel by ©鳩摩羅童子 on 2011/12/3)
Peaucellier linkage wheel ,,⚫ = axis, ■ = ground, ◯ = fixed cam (lozenge head slides on surface of it.)
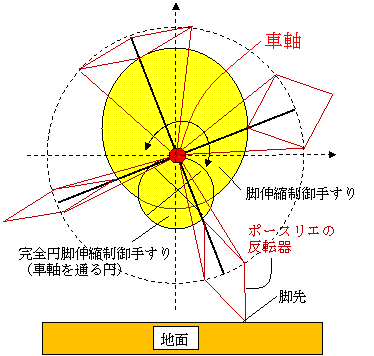
左図は、ポースリエのリンクの菱形の伸縮を脚とした車軸水平維持移動のサンプルである。シンプルである。
車軸および脚伸縮制御手すりは、台車筺体に固定する。
菱形は横にペチャンコとなる様に頭を押すと、脚は縮む。
【手すりは菱形の頭の押さえ付けを加減する(= 一種の固定カム)。手すりの壁の車軸からの距離が大きい程、菱形は横にペチャンコ。
左図では、脚の戻りの車軸より上にあるとき場所を取らない様にわざと脚を縮める様に手すりの車軸からの距離を大きくした例を示した。】
もし、この車輪を誰も作ったことが無いなら、作って広めて下さい。
(キャスター、荷車、自転車のデモ版を作って下さい。)
----- Google 検索によると、まだ誰も左記車輪の記事は書いていない様に見える。
(日本国特許庁のDB を調べたが、ポースリエ 3件、ポ-セリエ 1件。→ 皆、該当せず、だった。)
--- もし、私が第一提唱者なら、引用する際は私の名を付記しておいて下さい。
左図は、4本足の例で車軸から下方向左右45゜の範囲(計90゜)を一つの脚の守備範囲とみなしている。但し、手すりの完全円の部分は余裕を取り、ほぼ左右90゜分は完全円とした。
【誰か計算してみて下さい】 O is fixed point with hinge.
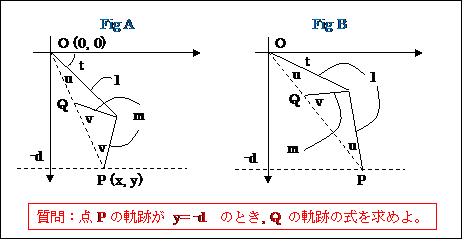
左図の FigA の点Q の軌跡は円だとポースリエさんは言っていますが、本当ですか?
曲線の式を x, y, l, m, d で表して下さい。--- かなり難しい!!。
私は途中で断念しました。多分、ヘロンの公式の様な式になる。
予定は、x2 + (y + r)2 = r2
[r の値はどうなる??]
ついでに、FigBの点Q の曲線式も教えて下さい。
私の予想では、円か楕円かその他。
Fig-A
OP = l*cosU + m*cosV, OQ= l*cosU-m*cosV, l*sinU=m*sinV
Px= OP*cos(T+U), Py= -OP*sin(T+U) --- Py=-d i.e. OP*sin(T+U)=d
X= OQ*cos(T+U), Y= -OQ*sin(T+U)
-----
T消去
Y=-OQ*sin(T+U)=-OQ*d/OP=-OQ2*d/(OQ*OP)=-OQ2*d/(l2-m2
) --- ①
X2=OQ2*cos2(T+U)=OQ2*(1-sin2(T+U))=OQ2-Y2=-[(l2-m2)/d]*Y -Y2 (by ①)
∴ X2 + Y2 + [(l2-m2)/d]Y =0 --- X2 + (Y + [(l2-m2)/(2d)])2 - [(l2-m2)/(2d)]2 =0
よって、r = (l2-m2)/(2d) で、X2 + (Y+r)2 = r2 案外簡単だった。
OQ*OP=一定 の magic を知っていると早い。
【(X-0,Y-0)内積(X-0,Y+2r)=0 ---- 点O(0,0) と点S(0,-2r)= (0,-(l2-m2)/d)からのベクトルが直交する軌跡
--つまり、点O, S を直径とする円。 d が大きくなるとすごく小さい円になりますね。】
提案:この問題、高校の教科書の問題の中に入れて下さい。解法指針が無いと、無限ループして解けない。思考訓練向き。
結果は円ですが解析的証明して下さい、と問題提示すると良い。
コメント: ポースリエのリンク直線軌跡は、2つの公転円のなせる技。また、点 O, Q, P は一直線上の colinear。
============
Fig-B
OP=2l*cosU, OQ=l*cosU-m*cosV, l*sinU=m*sinV
OQ2=l2(1-sin2U)+m2(1-sin2V)-2lm*cosUcosV = l2+m2-2m2*sin2V -2lm*cosUcosV
X2+Y2=OQ2
Y=-OQ2*d/(OQ*OP)=- OQ2*d/(2l2cos2U-2lm*cosUcosV)
=- OQ2*d/(2l2-2l2sin2U-2lm*cosUcosV)
=- OQ2*d/(2l2-2m2sin2V-2lm*cosUcosV)
よって、
l2+m2-2m2*sin2V -2lm*cosUcosV = X2+Y2 ---②
2l2-2m2sin2V-2lm*cosUcosV = =- OQ2*d/Y =-(X2+Y2)d/Y ---③
②-③:X2+Y2 + (X2+Y2)d/Y = m2-l2
i.e. (X2+Y2)(1+d/Y)= m2-l2 ---- (X2+Y2)(Y+d)= (m2-l2)Y --- X2+Y2 = (m2-l2)*Y/(Y+d)
∴X2 = -Y2-(l2-m2)*Y/(Y+d) ∴X = sqrt[-Y2- (l2-m2)*Y/(Y+d) ] --- 何コレ?
cf. Exploring Linkages -- The development of the straight-line linkage
cf. Mathematical Aspects of the Peaucellier-Lipkin Linkage (これ面白い)赤道→円、北半球→外側、南半球→内側、be congruent to 合同、be similar to 相似、conformal 等角、北緯=南緯の±同緯度ペア→inversive pair 形成
cf. 研究授業事前課題 (.pdf)
(C) copyright~御協力ありがとうございました、
筑波大学大学院修士課程教育研究科、
保坂高志 竹谷正 野口敬子
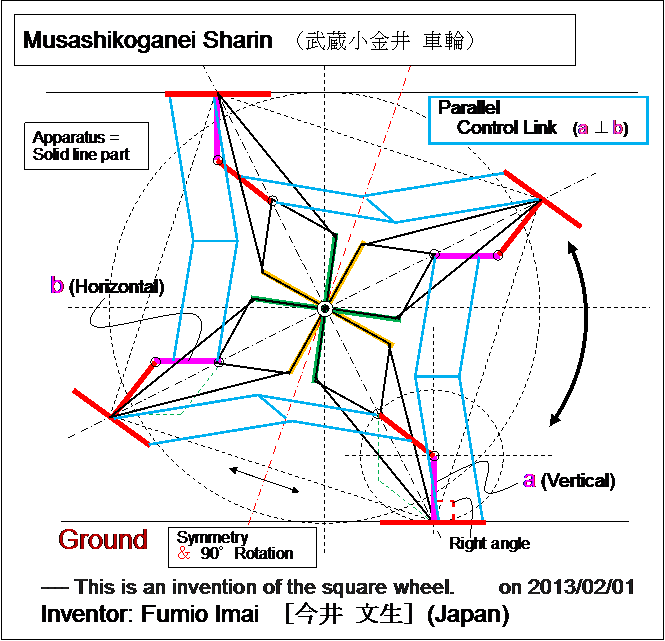
■ 武蔵小金井車輪
前記ポースリエ車輪の強化版を示します。
「四角い車輪」の発明です。
教科書に載せて下さい。
2020/03: 修正する。blue Parallel control link は、多分、削除可能。足が地面、天井以外の中間水平位置のときは、
pink は、常に水平。つまり、水平 or 垂直の基準の仕組みが得られれば、追加 bar は不要。
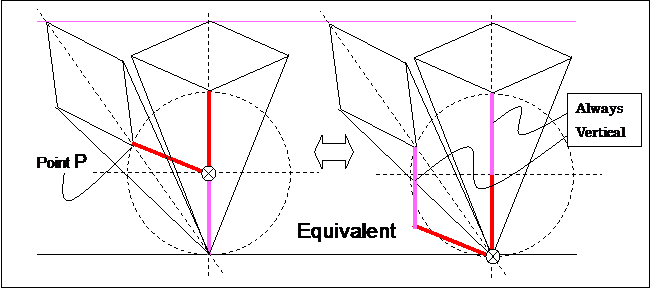
正方形の中の一点鎖線が完全横十文字に成る critical 地点直後、 pink の水平を保証すれば良い 、だけ。円の上半分の外側に囲いの手すりのドームを付け、垂直のままの足底を倒すように誘導させる。なので、blue は完全除去可能。足のくるぶしは、破線円からみて、垂直移動、垂直接線は水平直径の端。
・ 足のくるぶしは、端に有るべきで、中央に有ってはいけないのです。自然の摂理の結果なのです。クリティカルポイントは、発生しない。
2020/04/05 中央くるぶしは、対称性&強度の観点から、好ましい。blue Parallel control link の棒の数 5×4=20 は、1+3×4=1+12=13 に出来る。
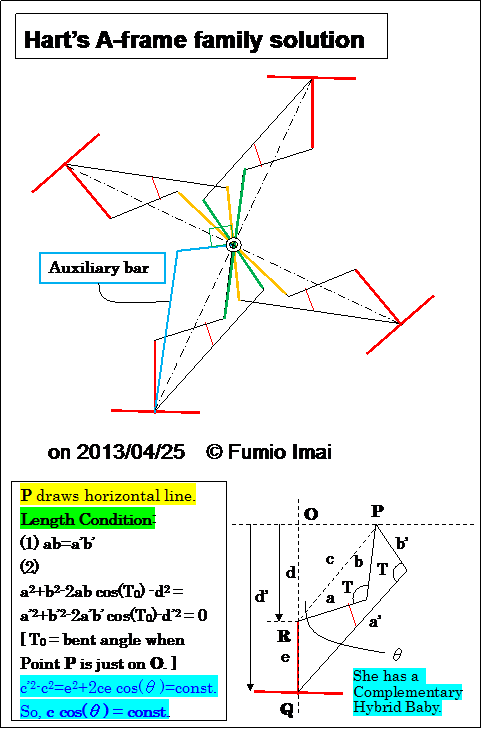
一般化 Hart's A-frame の適用への変化。 こちらの方がシンプルな結果となった。
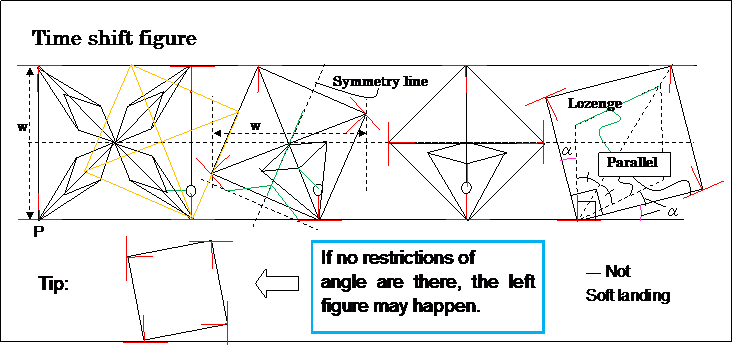
等高・可変長・正方形転がし
である。
脚の地面角度が 45° なので、チェビシェフ車輪よりも、
long stride である。
Hart's A-frame Wheel (GeoGebra)
(左図は厳密には補助棒が一部不足している。
今頃判明した。 on 2016/08
GeoGebra に投稿した図は正しい。)
2018/05 発見。: この図は正しい。
さらに、補助線棒が無い実装も可能。
(→ コレは、頭の体操です。)
左図は、一点鎖線 -・- の十字架に対し、
45°線に関し、完全な線対称。理解しやすい。
でも、賢くない。
→ 左下の右側に倒れている2組の折れ線棒を、
一点鎖線に関し、左側に倒す(等価)。
すると、補助線棒を兼務する形になる。
(つまり、点対称と線対称、90°回転と、のチャンポン)
卍手裏剣(まんじしゅりけん)のような形になる。
一般化 チェビシェフリンク の適用への変化。チェビシェフリンク車輪の最新版。
旧方式の今一さが、無くなって、実用レベルへ昇格した。
Peaucellier, Hart の車輪のアナロジーを考えることにより打開策がポロリと出てきました。
多分、発想を変えなかったらこの解は幾ら考えても出て来ないと思う。
面白い性質を有す。
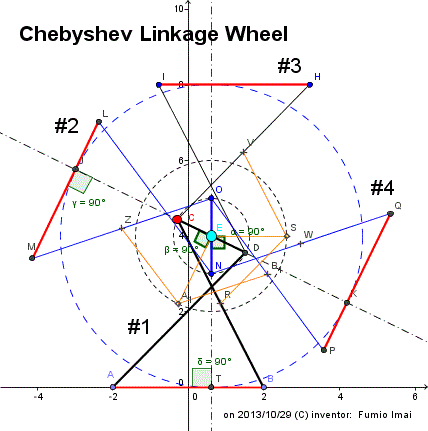
代わりばんこ背負い投げ方式です。
--- GeoGebra サイトに worksheet を登録した
ので、DEMO 体験できる。
詳細は下記を参照。
Musashikoganei Square Wheel
補:ABCDEFG・みんなのアイデア発明掲示板 に投稿した際、下記質問を受けました。
回答案を下記に記す。理解向上の参考にして下さい。
>from たかはし 様。
>このアイデアの実用性はなんですか?
①接地部面積が広い車輪。
ex. 浜辺・ジュータン・向け車輪。
②摩擦が少ないキャタピラ機構。(下敷き背負い車輪、摩擦は連結回転部のみ)
---- 従来タイヤにポースリエ車輪又はハートA-frame車輪の板を軸を合わせてはめると、板状のスノウ・チェーンと言った感じになる。 ---- このとき、タイヤと板は圧着位置がタイヤの円周上を移動していく感じ、擦(こす)れることは無い。優秀!!
(チェビシェフ車輪の板をはめると、タイヤとの擦(こす)れが発生してしまうので駄目。)
(ポースリエ/ハート:板の長さは、つま先側とかかと側を高さの半々にすると、共に先が地面にぶつかってしまう。
従って、約 80% の長さにする必要がある。地面の板の接続部に 20% の空きが生ずるが、タイヤが陥没は多分しない。何故なら残りの80%の板で軸の高さが保持されているから。)
---- 長さは 100% で、 80% の両端にゲタの足を下に付け、板を地面から少し離すのも良いみたい。ゲタ状板対策。
(正方形から正六角形の6枚化にすると足の裏の長さ問題は無い。しかし、部品数が増え、問題。)
イメージ: 正方形の段ボールの中にタイヤを置き、このをタイヤを転がす、と言ったイメージ。座布団を4枚用意して、自分で座布団を置き、その上を通り、通り過ぎたら座布団は回収する、これの反復。。
・ 径の小さい旅行カバンのキャスターにこれをはめ、疑似的に接地面を大きくすると、キャスターの引きずり騒音が緩和するかも知れない。
・ 非常に重い荷物を載せる台車の車輪に、この板輪っかをはめると、地べたの凹(へこ)みは緩和される。
③折り畳み式車輪(普段は棒の束、緊急時用場所喰わず車輪、自衛隊向け?)
④数学・理科教材
----- 直線描画リンク機構、チェビシェフリンク・ポースリエリンク・ハートの A-frame
----- 四角い車輪の存在することの認識。
Chebyshev N=2 wheel
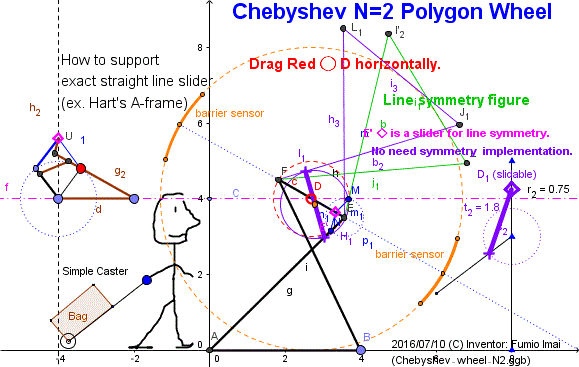
代わりばんこ背負い投げ方式です。
--- GeoGebra サイトに worksheet を登録した
非常にシンプルである。
r2 = 1 のとき、線対称の結果と 99% 近似。
2つのチェビシェフリンクを背中合わせにして、かすがい棒1本を追加するだけで実現。
(カスガイ棒はコの字型にすると軸 D ◯ と衝突しない。)
Chebyshev_walker
Chebyshev linkage application.
Bi-pedal walking apparatus.
Catch the Red bullet B ●, then Please rotate it.
Chebyshev parts/ leg = 4 bars (each length 4,5,5,2)
Crank parts/ leg = 4 bars (each length rr,rr, long [ex. =5], 2.5)
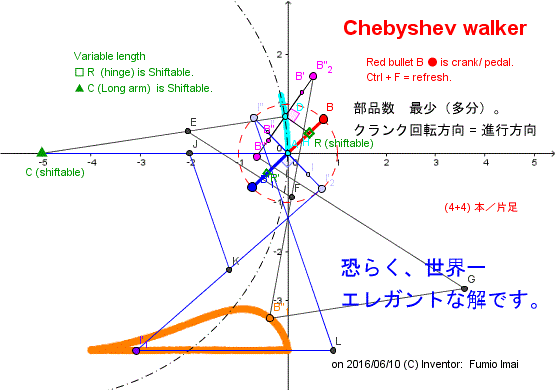
往(0°~180°): 軸は固定(縮退)
復(180°~360°): 軸は上下
where,
AR = rr, BD = rr --- 可変長
B'B" = 2, B'B"1 = 5, B"1G =4, GB" =5
ED = 2, EF = 2.5
cf. 通常の実装法 sample:
TLT15 [チェビシェフリンク2足歩行ロボット]
--- 後ろ向きクランク回転なのは、感覚的にはダメ。
CD を長くすると、水色の上下軌跡は、垂直線に近づく。すると、橙色の足の軌跡は、左右対称の山型に近づく。
Perhaps, This is very elegant solution in the world. (?!)
Fumio Imai, 10 June 2016, Created with GeoGebra
Chebyshev_walker.gif (18.0 KB)
GeoGebra DEMO (IE で実行) Chebyshev_walker.html
(↑ Java Applet なので、実行ガードあり。 Java コントロールパネル/セキュリティ/非常に高い(V)、 の指定要。また、例外サイト・リストに http://jars.geogebra.org/ と http://www5d.biglobe.ne.jp/ の追加要。)
----- GeoGebra に worksheet を登録したので、それを動かしてみるのが browser 制限も無いのでいいかも。「Chebyshev_walker」 というタイトルの作品です。
(バカ Java/ Oracle を相手にしなくていいので、非常に楽。今までの作品も全部登録しようか?。)
■三日月型軌跡クランクの発明と応用
長年捜していた完全円を含む三日月型の描画リンク機構を考え出した。
これにより、ポースリエのリンク機構を歩行ロボットに適用できるようになった。
(我ながら、自分で言うのもおかしいが、これはスゴイ発明である。)
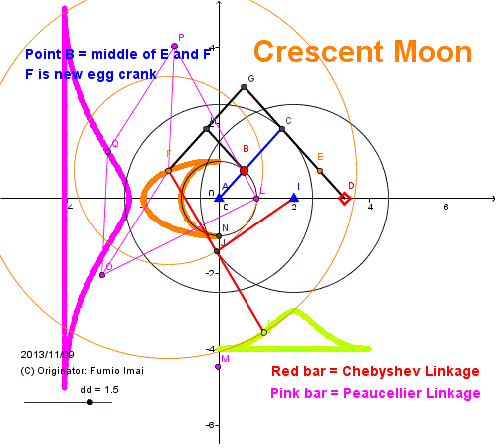
三日月型軌跡のクランクの完全半円部がポースリエ/チェビシェフのリンクにより直線にマッピングされる。
楕円部は折り返し脚部の軌跡(現在は、すり足)にマッピングされる。
本当は、楕円では無く、もっと外側に膨らんだ曲線にしたいのだが、構造が複雑になる。
左図のミソは、太黒線のフレームが、左半面では縮退 (shrinking) して一本線になり、昔の動きをすることである。
左記三日月描画リンク機構は世界に今迄存在していない。
∵ もし、あったらこんな苦労はしていませんワ。
c. 半円の制限をとり、部分完全円弧(ex. 180゜ の半円では無く 90゜ の円弧)、にしたいが、やり方が未だ見つからない。
(誰か、もし良いやり方を見つけたら、公開して下さい。)
Here is the Anchor name = "a=b". ---- Alias: Musashikoganei 49-frame
I introduce to you the/ MY 9 bars exact straight line drawing apparatus.
(This apparatus comes from 3D 4 bars exact straight line drawing apparatus.)
Detail is below.
Generalized Hart's A-frame Online DEMO (© F.IMAI, GeoGebra Java applet)
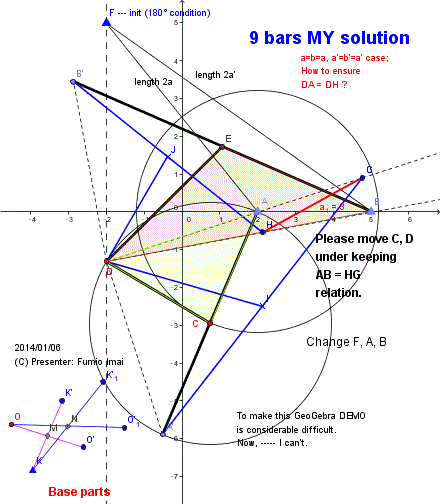
- Fig.1C_a=b -
This is educational.
Why does this work correctly? ---- Please consider.
左図は Hart's A-frame が対応できない a=b のケースの解である。
5本が9本に倍増する。
二重構造になっている。基本部品(Base parts)を2組使用する。
1組だけでも3次元環境下で2次元下に直線を描画できる。
(【証明】完全な二重対称性を保証しているので、直角三角形の高さは同じ。なので、正確な直線が保証される。)
左図の例は、凸の口ばしの例であるが、ウッドペーッカー(きつつき)の口ばしのHart's A-frame タイプの凹にも変更できる(凹凸の二種を楽しめる)。
詳細は DEMO で確認して下さい。
- Fig.1C_a=b -
Another sample answer. 9 (or 10) bars Closed loop. on 2020/12/11 added.
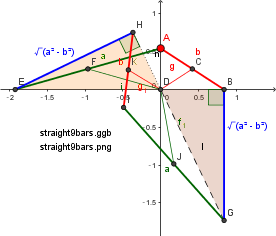
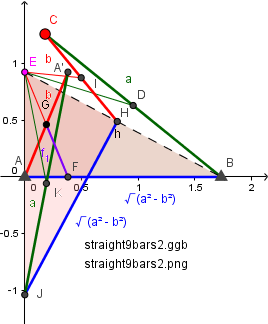
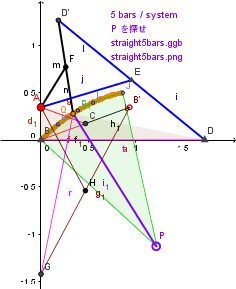
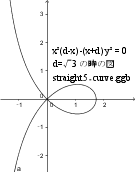
orange color point Q trace is near a circle.
Please prove. so, we can realize 5 bars/ system. on 2020/12/19 by F.IMAI
D=(0,d)
A=(0,z)
Q=(x,y)
x^+(z-y)^=z^ ①
y=(-z/d) x +z ②
from ②
y=z[(-1/d)x+1]=z(-x+d)/d
∴ z= dy/(d-x)
x^-2zy+y^=0
then
x^-2[dy/(d-x)]y +y^= x^- 2[d/(d-x)]y^+ y^= x^ + [1-2d/(d-x)] y^ = 0
x^(d-x) +(d-x-2d) y^= x^(d-x) +(-x-d) y^ = x^(d-x) -(x+d) y^ = 0
円弧では無かった。3次関数だった。レムニスケート(英: lemniscate)似。
cf. デカルトの正葉線 --- ほぼ同類。
cf. 正葉線 ---- この site の図から、推測すると、正葉線は 45 °の y=±x と接する円弧が近似。半径は、d 臭い。
つまり、上の straight5bars.png の図の 点 P は、(d/√2,-d/√2) 臭い。原点B から 45°右下長さ d の位置。
--- 近似は、原点近傍では完全一致。x が大きくなると、少しズレテいく。P をほんの少し右上にズラシテ補正すると、ほぼ完全一致。実用には多分判別不可だろう。 なので、5 本の疑似直線器の解と言える。
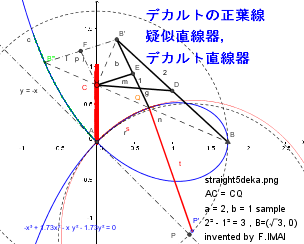
• 逆に、デカルトの正葉線の葉の端の点B(d,0) からの直線と y 軸との交点を C, 正葉線との交点を Q 、xy 座標の原点を A とすると、QC = AC で、線分の長さは常に等しい。みたい。 -- (a)
BC と QC の長さの2乗の差は、常に一定。-- (b)
Q から直交線を引き、x 軸との交点を Q' とすると、QQ' = AQ' -- (a')
• この装置を定規と共に逆に適用すると、正確なデカルトの正葉線が描画できる。
■武蔵小金井自転車™
二足歩行リンク機構の「武蔵小金井脚 ™ Musashikoganei Leg ™」の応用例。
水平ピストン運動機構に、クランク(ペダル)と剛体脚(直角三角形+円弧足)をつなぐと、二足歩行機構が容易に実現される。
---- かなり優秀?。
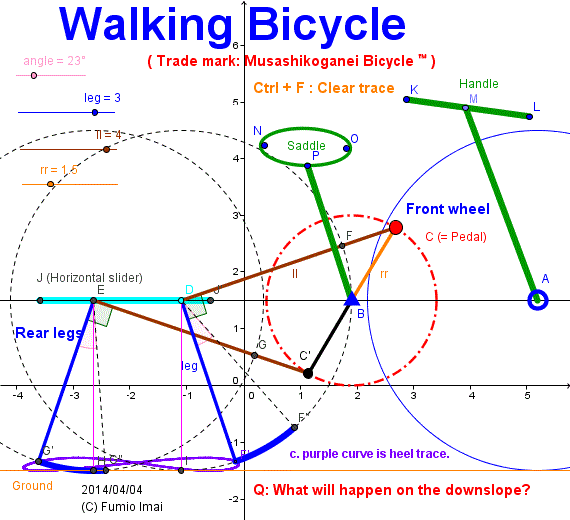
- Centipede_bicycle.gif -
Maybe Tired exercise ???
Q: on the downslope?
A: perhaps, passive automatic walking endlessly.
(--- It's evident (?).)
If tri(= 3)-legs were supported, more smooth downward action will be realized. but it becomes complex structure (so, I don't recommend).
[i.e. Please make 120°-120°-120° triangle crank pedal. ]
This is a
Musashikoganei Leg
application.
- Centipede_bicycle.gif
Imai's Hart's A-frame Leg
可変長二足歩行
現時点で、リンク機構の理論解としては、世界一の方式だと思う。
詳細は下記へ。
Musashikoganei Square Wheel

- Centipede_A-frame_stroke_1.gif -
Left apparatus has no angle check controller.
No angle dependent parts.
but, acts correctly.
I did nothing except procedure to usual A-frame. Left is usual/ ordinary A-frame itself.
- Centipede_A-frame_stroke_1.gif -
Imai's linkage (alias, Crescent mapping leg.)
今井・リンケージ(別名:三日月形写像の脚)
チェビシェフ・リンケージ[疑似直線描画リンク機構]の親戚。
(---- チェビシェフリンク機構の概念を二足歩行実装用にその概念をさらに拡張・特化したものです。)
c. 戻り(復路)のストロークはクランク角の約 1/4 の角度、行き(往路)は 3/4 の角度を占める。
つまり、復路は往路の三倍のスピードで戻る。足は 75% の確率でいつも地面の上に居る。
c. tri-pedal 版もかなり良い性質を有しています。DEMO (13-g) を見て下さい。
3本の足の内、2本は常に地面上にある。 ----- つまり、脚 1式(1個)で、荷台の水平性を保証する(かなりのスグレ物 (?) )。
(3本が同時に地面に居るときも有る。)
中間の三日月は、膝関節の半月板, 別資料、に形・目的ともに近いと思う。凹型レンズにも似ている。
荷重を掛けると左右対称で無いので弱いように見えるが、これは誤りである。実装は、M、Xのフレームで半月版の軌跡を実装できるので、構造的には強くでき得るが、3次元環境ではかなり困難。
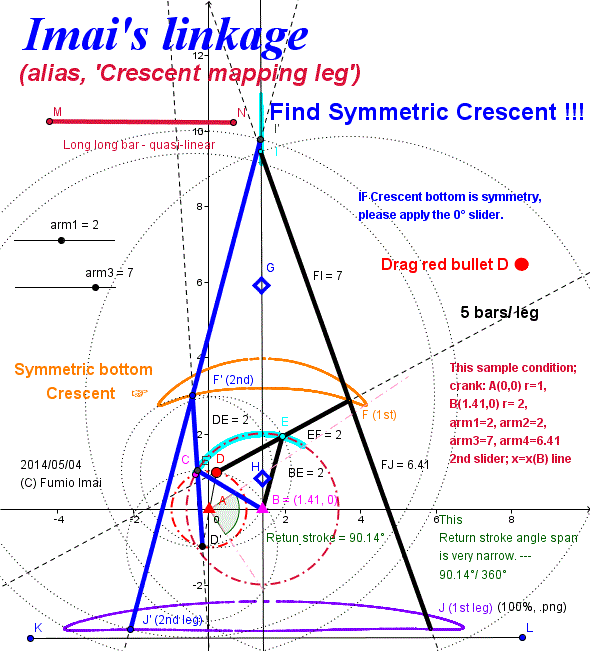
- Centipede_Cheby_45_slide_symmetry.gif -
★ 2017/12/11 下記コメント追加した。
だいだい色の三日月 は、必ず y 軸線対称である。
直感的にも、
点 D の x 軸対称のクランク円 を、
点 B を中心に、右 90° 回転し、D を F に mapping.
BD ⊥ BF
但し、BD2 + BF2 = 一定
なので、F の軌跡は必ず y 軸線対称。
-- 代数的にも証明は簡単。
- Centipede_Cheby_45_slide_symmetry.gif -
★ 2018/01/23 上記 Imai's linkage よりも、同じ 5 bars で、もっと賢い方式を発見した。下記がそれ。
着地の足の角度が地面と直角。海岸の砂の上を歩ける。 bars の数は 5 本のまま。
(従来の実装の状況を web で調べたが、下記方式は、シンプルで最強である。かなり賢い。
三日月では無くオリジナルの Chebyshev Linkage そのもの。
発想としては、5 bars Hart's inversor 直線描画機構に近い思考回路の成果。
上記 三日月方式が自分では 5 bars で最強だと思っていたが、そうではなかった、と判明。)
cf.
Chebyshev's Lambda Mechanism のアニメーションの実装は、賢く無い。単体 crank では無い方式。
(∵ 前後並行2本足を実現するのに crank は2つも要らない。下記方式で、茶色の q の垂直1本足を2本足にするだけで良い。 crank 数は 1 のまま。)
cf.
Klann linkage 5 bars. 単体 crank。 本体の上下動あり。 左記サイトに Jansen Linkage のアニメーションもあるが、Klann linkage 共に、よく見ると、両方共賢く無い。下記方式の方がスマートで賢い。

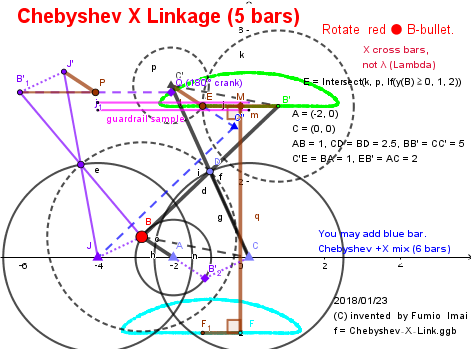
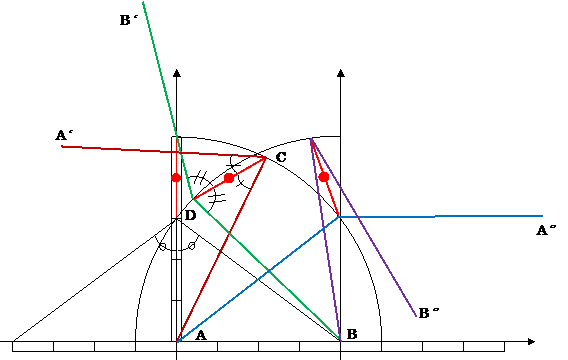
- Chebyshev_X_Link.png -
BC // C'B' and,
△ABC ≡ △EC'B' , so, EB' // AC
Very Good !!!
Geogebra のサイトに登録した。
動作確認したい人は飛んで。 link.
Imai's Watt's linkage vertical Leg walking Toy on the slope
今井・ワットのリンク機構、下り坂を歩く垂直足おもちゃ
cf. Musashikoganei Square Wheel
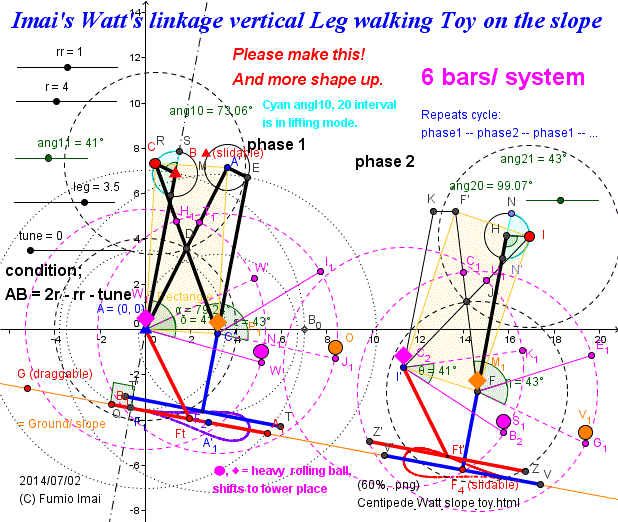
- Centipede_Watt_slope_toy.gif -
phase 1: 赤の左足 は地面についている、そして、青の右足 は浮いており、右足の上を越えようとしている。
phase 2: バトンタッチ後。 phase 1の逆。右脚が地面、左足がその上を跨ぐところ。
脚軌跡の形はレムニスケート(連珠)曲線の上半分の部分。
売り:
長い歩幅。6本バー/システム(コンパクト構造)。
■ ボールの重りのカラクリは、多分必要。軸足になっている片足のみに、重りを移動させる。渡り廊下の機構必要。
i.e. ball は全体で1個。赤を右足。青を左足とする。左図の左側の図では、今、赤が軸足。AA' の対角線の根本の右側に ball を配置。ball の重みで、AA' を右回転させる力が働く。青を持ち上げ、Xを伸ばす。最高に伸びた時、青の右足は地に付く。両足が地に付いている時 ball を 青の根本へ移動させ、棒 CC' の根本の右側に配置。 ball の重みで、CC' は右回転し、Xは縮む。赤は持ち上がる。最高に縮むと、両足は合わさって地に付く。 ball を根本同士間で反対足に移す(ズラす)。
ball はそのまま堅持、同じ軸足で、反対線の棒を伸ばすサイクルに入る。( ball の移動は、両足が離れて地面に来た時のみ。) --- 対称性から考えると、両方共正しい様に思うが、ハッキリしない。コレ、難しい。--- 361° にする時、Xが左側に戻らず、右側へ行く(象限移動のトリガ)押す力が必要だネ。
これで1サイクルが終わる。
(坂が傾いていれば、X字の長方形パンタグラフも常に傾いているので、自重で長方形が自動的に(ゆっくり (?))伸びる・縮む、する。との、希望的観察は、誤り(?)。 重りは、相手を持ち上げるために必要だが、支えを安定させるためにも必要なので、もう一つ別の重りが有った方が良いかも。2種の重り以外をすごく軽し、重りは重く、すれば無限ループの再現は容易な気がする。
繭玉をいくらスロープに置いても起き上がりこぼしにはならない。中に重りが必要、と同じ。)
--- 誰か、現物を作って下さい。繭玉よりは、両足が動くので面白い。多分。
【断言するが、繭玉の起き上がり小法師は、無限にスロープを下っていく、通常、途中で止まらない。2足歩行のおもちゃも同じである。途中で止まるのは、造りが悪いからである。方式が良ければ、絶対に止まらない。ギネスブックの記録更新なんて、本当はチョロイ。と、私は考える。】
c. |X|の frame の2つの縦棒 |,| の片方の棒を手で持って、横(垂直以外、斜めも良い)にすると、X の形で自重の重さで、他方の棒は、水平に落ち、ぶら下がりが伸びる。なので、坂の角度を急にすれば、軸足さえしっかり固定されていれば、自重で伸び縮みする。重りなんて要らない気もする。重りは、軸足の支えを代わりばんこに固定するのを助けるために必要で、伸び縮み促進のためでは無い、とも言える。いずれにせよ、本方式は feasible な気がする。片足で倒れず持ちこたえられるか否かが問題。
- Centipede_Watt_slope_toy.gif -
Q: チェビシェフリンクとほぼ同じ蒲鉾形で、クランクと同じ回転方向で、底部がもっと直線に近い曲線、そんなリンク機構はあるか?
A: ---- ある。
cf. Musashikoganei Square Wheel
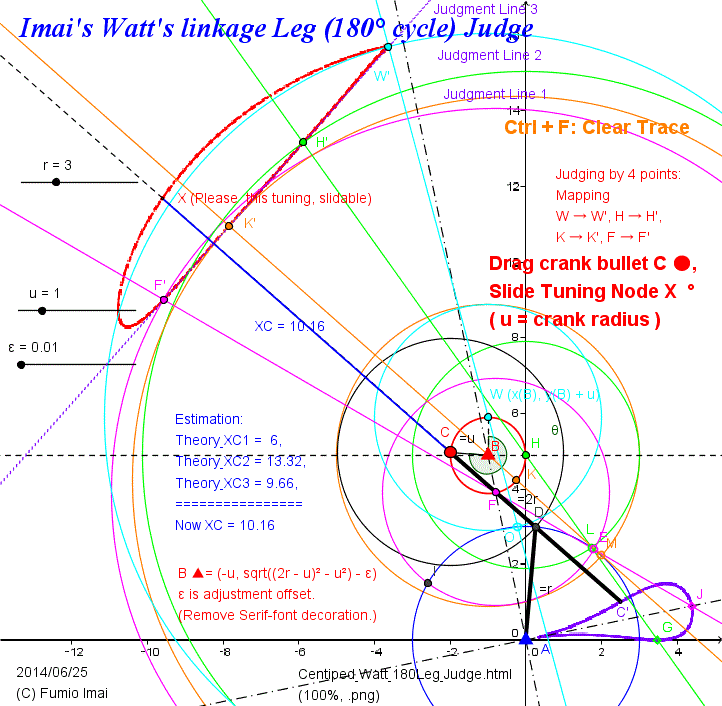
- Centipede_Watt_180Leg_Judge.gif -
- Centipede_Watt_180Leg_Judge.gif -
Link free. (C) 2013, F.IMAI , All Rights Reserved.


 - Chebyshev_X_Link.png -
- Chebyshev_X_Link.png -





 チェビシェフ・リンクの棒の長さの比 4:5:2 の比は、ペダルが垂直から 180°回転する時の 0°, 90°, 180°のペダル角度の時の中点の高さが等しい為に、ほぼ直線に見えるカラクリになっている。
チェビシェフ・リンクの棒の長さの比 4:5:2 の比は、ペダルが垂直から 180°回転する時の 0°, 90°, 180°のペダル角度の時の中点の高さが等しい為に、ほぼ直線に見えるカラクリになっている。




























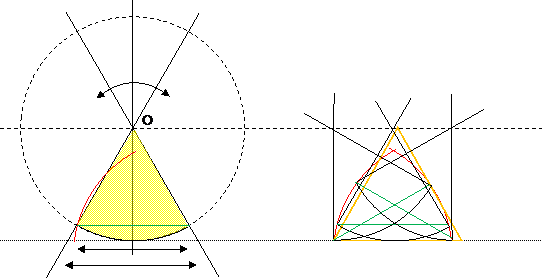








 ∠ は、約 45° より小さくなったら、0° と予測して良い。
∠ は、約 45° より小さくなったら、0° と予測して良い。







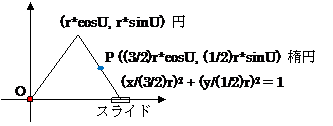






 ① M を固定したと絶対的に見ると、H を M を中心に回転、すると P が Q の接線上を移動。
① M を固定したと絶対的に見ると、H を M を中心に回転、すると P が Q の接線上を移動。
 左図は、基準点 O (0, 0) と A (a, 0) の長さ a の線分の内分点 P を可変的に移動させるリンク機構があることを示す。
左図は、基準点 O (0, 0) と A (a, 0) の長さ a の線分の内分点 P を可変的に移動させるリンク機構があることを示す。 2点間線分のオーソドックスな描画法は、左図である。
2点間線分のオーソドックスな描画法は、左図である。